Grundläggande sannolikhetsfråga matematik 5 - Venndiagram tänk

Tva servicestationer betj änar kunder. F ör vardera av de tv å stationerna g äller att sannolikheten att det
ska uppsta k ö ar 0.1 medan sannolikheten att det är kö vid b åda samtidigt är 0.04. Ber äkna sannolik-
heten att ingen av stationerna har kö

Mitt tänk: Jag tänker att man ska tänka det i venndiagram men har jäkligt svårt att rita upp rätt venndiagram.

Det är 0.96 att det inte är kö hos båda samtidigt. Det är 0.9 att det inte är kö i kö 1 då. Det är 0.9 Att det inte är kö i kö 2.

0.96*0.9 eller något sånt tänker jag då kanske borde rätt svar. Men det blir extremt fel!

Kalla stationerna station ett och två. Ett kan vara öppen eller stängd, samt att två kan vara öppen och stängd. Det ger följande möjligheter i ett litet schema:

$\begin{matrix} {IK}_{1} & K_{1} & Totalt \\ {IK}_{2} \\ K_{2} & 0, 04 & 0, 1 \\ Totalt & 0, 1 & 1, 00 \end{matrix}$

Vad är sannolikheten att det är kö vid den ena men inte vid den andra, om den totala sannolikheten för kö ska vara 0,1?

Sannolikheten att station A har kö är $Prob(A) = 0.1$ .
Sannolikheten att station B har kö är $Prob(B) = 0.1$ .
Sannolikheten att båda stationerna har kö är $Prob(A \text{ och } B) = 0.04$ .

Det som efterfrågas är sannolikheten att ingen station har kö, vilket är sannolikheten $Prob(\text{Ej A och Ej B})$ . Enligt de Morgans lag är denna sannolikhet lika med $1 - Prob(A \text{ eller } B)$ och enligt Additionssatsen är $Prob(A \text{ eller } B) = ...$ vilket ger

$Prob(\text{Ej A och Ej B}) = 1 - Prob(A\text{ eller }B) = ...$

Går det inte rita ut i ett venndiagram?

Uppskattar bådas sett att hjälpa men är fortfarande inte helt säker..

Kvadratenskvadrat skrev:
Går det inte rita ut i ett venndiagram?

Uppskattar bådas sett att hjälpa men är fortfarande inte helt säker..

Jo det går att rita Venndiagram, men varför vill du göra det när du i slutändan ändå måste beräkna en sannolikhet? Händelsen "Ej A och Ej B" är ju området som ligger utanför unionen "A eller B" i ett venndiagram, men hur hjälper det dig att beräkna sannolikheten? Du behöver ju relatera denna bild till de givna sannolikheterna på något sätt och då hamnar du i de beräkningar som jag skrivit.

Går det inte rita ut i ett venndiagram?

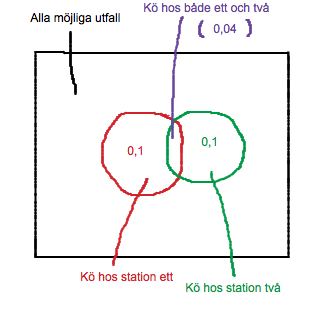
Jodå, försök! Rita upp ett Venn-diagram med två "ringar". Du vet att varje "ring" är värd 0,10 och att det överlappande fältet är värd 0,04. Räkna ut värdet för de båda delarna av ringarna som inte överlappar varandra. Summera de tre delarna. Sannolikheten för att ingen av stationerna har kö är 1 - (denna summa).

0.1 den ena + 0.1 den andra - (0.04 som överlappar) = 0.16

1-0.16=0.84

Är det åt rätt håll?

Det stämmer bra!

Utmärkt hjälp smutstvätt. Oerhört tacksam för detta

Varsågod! :)

Svara

Visa senaste svar