Gruppteori: diskreta grupper

Du har markerat att du är nöjd med hjälpen. Var detta ett misstag, eller har du hittat lösningen någon annanstans? Om du fortfarande behöver hjälp, kan du ta bort markeringen genom att trycka på "Avmarkera".  /Smutstvätt, moderator 

Jag har inte fått någon hjälp men jag är nöjd ändå, jag kom på svaret själv.

Okej, vad bra!

Lemmat handlar om begreppet gitter (eng. lattice), som syftar på delgrupper av $(\mathbb{R}^d,+)$ som är isomorfa med $\mathbb{Z}^d$. Varje gitter kan uttryckas på formen $\mathrm{\Lambda} = \{n_1\mathbf{a}_1 + \cdots + n_d\mathbf{a}_d:n_1,\ldots,n_d\in\mathbb{Z}\}$, där $\mathbf{a}_1,\ldots,\mathbf{a}_d\in\mathbb{R}^d$ kallas för gittrets generatorer.

Här har du ett exempel på ett gitter i $\mathbb{R}^2$ genererat av punkterna $\mathbf{a}=(1,4/3)$ och $\mathbf{b}=(1,-1/2)$. Notera att gittrets punkter utgörs av hörnen i mönstret - linjerna är egentligen inte en del av datan som specificerar gittret, utan är bara medritade för att visa hur gittret genereras av generatorerna.

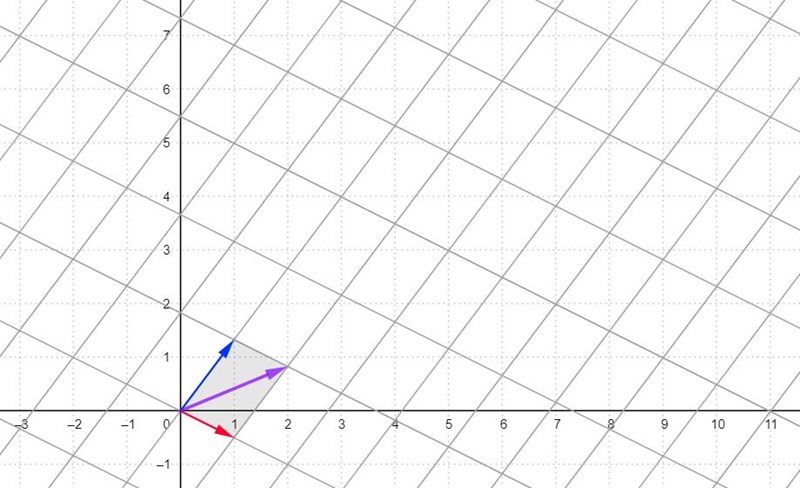
Lemmat säger att om vi har en delgrupp $\mathrm{\Lambda}$ av $(\mathbb{R}^2,+)$, och två stycken element $\mathbf{a},\mathbf{b}\in\mathrm{\Lambda}$, och vi misstänker att $\mathrm{\Lambda}$ är ett 2-dimensionellt gitter genererat av $\mathbf{a}$ och $\mathbf{b}$, så räcker det att visa två saker:

• $\mathbf{a}$ och $\mathbf{b}$ är linjärt oberoende
• parallellogrammet som spänns upp av $\mathbf{a}$ och $\mathbf{b}$ (dvs. mängden $P=\{s\mathbf{a}+t\mathbf{b}:s,b\in[0,1]\}\subseteq\mathbb{R}^2$, gråmarkerad i exemplet ovan) inte innehåller några fler punkter från $\mathrm{\Lambda}$ än parallellogrammets hörn (dvs. punkterna $\mathbf{0}$, $\mathbf{a}$, $\mathbf{b}$ och $\mathbf{a}+\mathbf{b}$).

oggih skrev:

där $\mathbf{a}_1,\ldots,\mathbf{a}_d\in\mathbb{R}^d$ kallas för gittrets generatorer.

Exakt det jag anade, synd att mitt kompendium aldrig använde det ordet.

Jag hade först lite svårt att fatta "... delgrupp av $\displaystyle \mathbb{R}^2$" tills jag insåg att avskalade vektorrum också är grupper. Tack för ditt svar!

Det kan apropå ingenting vara värt att notera generatorerna för ett gitter inte är unika.

Övning: Ge exempel på flera olika uppsättningar generator för det 2-dimensionella "standardgittret" $\mathrm{\Lambda}=\mathbb{Z}^2$. Rita gärna upp plottar för varje uppsättning generatorer du hittar, i stil med figuren ovan (t.ex. genom att använda den här GeoGebra-appleten). Lägg märke till samma hörnen i figuren är samma oavsett vilka generatorer man använder, även om mönstret kan de väldigt annorlunda ut.

Oj, så konkret som med geogebra behöver jag inte jobba. Det är väldigt analogt med vektorunderrumsbaser vilket jag är bekväm med. 

Eftersom "faktorerna" $n_i$ är godtyckliga heltal kan "basvektorerna" göras till vilken "multipel" som helst och fortfarande "spänna upp" samma "underrum".

Eller i gittersammanhang: eftersom heltalen $n_i$ är godtyckliga kan de genererande elementen multipliceras med vilka heltal som helst och fortfarande generera samma gitter.

Det går det väl inte alls

Qetsiyah skrev:

Eftersom "faktorerna" $n_i$ är godtyckliga heltal kan "basvektorerna" göras till vilken "multipel" som helst och fortfarande "spänna upp" samma "underrum".

Eller i gittersammanhang: eftersom heltalen $n_i$ är godtyckliga kan de genererande elementen multipliceras med vilka heltal som helst och fortfarande generera samma gitter.

Det går det väl inte alls

Preics - så enkelt är det inte! Problemet kan kokas ner till att koefficienterna kommer från $\mathbb{Z}$ som inte är en kropp (dvs. det finns inte multiplikativa inverser). Över huvud taget blir saker och ting betydligt svårare och konstigare när man går över från att göra linjär algebra över kroppar, till så kallad modulteori och homologisk algebra över generella ringar, så det här är bara början på om du fortsätter läsa mer algebra!

Men frågan jag ställde här är lyckligtvis ändå ganska enkel. Vågar du på dig ett nytt försök? Jag kan börja med att ge några mer eller mindre trivella förslag på generatorer, t.ex.

• $\mathbf{a}=(1,0)$ och $\mathbf{b}=(0,1)$
• $\mathbf{a}=(-1,0)$ och $\mathbf{b}=(0,1)$
• $\mathbf{a}=(1,0)$ och $\mathbf{b}=(0,-1)$
• ...men inte $\mathbf{a}=(2,0)$ och $\mathbf{b}=(0,-3)$, vilket vi redan har konstaterat (bland annat skulle vi missa gitterpunkten $(1,2)$).

Kan du ge några fler förslag?

För övrigt vill jag korrigera min definition av begreppet gitter en aning, för jag snurrade tvyärr till det lite i går. Den här definitionen borde göra jobbet:

Definition. Ett gitter av rang $k$ i $\mathbb{R}^d$ är en delgrupp $\Lambda$ av $(\mathbb{R}^d,+)$ på formen $\mathrm{\Lambda}=\{n_1\mathbf{a}_1+\cdots+n_k\mathbf{a}_k:n_1,\ldots,n_k\in\mathbb{Z}\}$, där vektorerna $\mathbf{a}_1,\ldots,\mathbf{a}_k\in\mathbb{R}^d$ är linjärt oberoende i $\mathbb{R}^d$.

Vi kan notera fyra saker:

• Här har jag tillåtit $k\leqslant d$ i stället för att kräva $k=d$, vilket verkar stämma bättre överens med ditt kompendium. (Notera att det inte kommer existera några gitter med $k>d$ i och med kravet på linjärt oberoende.)
• Vi får en gruppisomorfi $\mathrm{\Lambda}\to\mathbb{Z}^k$ genom att mappa $n_1\mathbf{a}_1+\cdots+n_k\mathbf{a}_k\mapsto (n_1,\ldots,n_k)$.
• Det räcker inte att bara säga definiera ett gitter av rang $k$ som "en delgrupp av $\mathbb{R}^d$ som är isomorf med $\mathbb{Z}^k$"; om vi inte kräver att generatorerna $\mathbf{a}_1,\ldots,\mathbf{a}_k\in\mathbb{R}^d$ är linjärt oberoende kan vi få en del lite småknasiga delgrupper av $\mathbb{R}^d$ som inte alls stämmer överens med vår geometriska intuition för vad 'gitter' borde betyda, men som likväl är isomorfa med $\mathbb{Z}^k$, t.ex. den här rackaren: $\mathrm{\Lambda}=\{n(1,0)+m(\sqrt{2},0):n,m\in\mathbb{Z}\}\cong\mathbb{Z}^2$.
• Ditt kompendium ger en - vid första anblicken - helt annan definition av vad ett gitter är, men den visar sig snabbt vara ekvivalent med vår definition:
  

Men frågan jag ställde här är lyckligtvis ändå ganska enkel. Vågar du på dig ett nytt försök? Jag kan börja med att ge några mer eller mindre trivella förslag på generatorer, t.ex.

Haha, nu tog du väl nästan alla? Den enda som är kvar är (-1,0) och (0,-1). Det är för att det inte finns miltiplikativa inverser, men det finns additiva inverser! Varje gitter har fyra baser?