Hållfasthet

Den här typen av uppgifter löser man med hjälp av Newtons rörelselagar (och matematik). Newtons första lag, NI, säger att om ett föremål är stilla eller rör sig likformigt så kommer det att fortsätta göra så, så länge det inte påverkas av någon kraft. I det här fallet har vi en låda som är stilla vid gränsläget 32$°$ lutning. Det betyder att den inte påverkas av någon kraft. Eller snarare, att alla krafter som verkar på lådan tillsammans har resultanten 0.

För att lösa uppgiften så börjar man med att rita en figur (precis som i videon). Det är mycket lättare att tänka rätt och inte göra misstag om man har ritat en bra figur. I figuren ritar man in alla krafter som verkar på lådan.

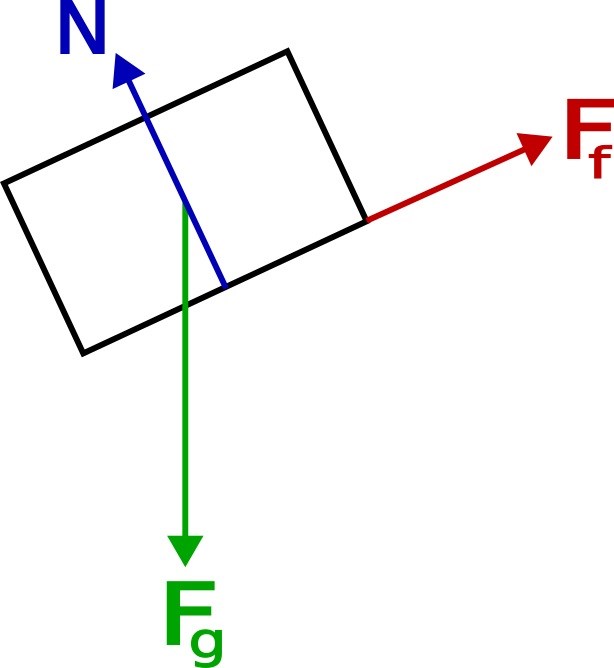
NI säger att summan av dem ska vara 0 eftersom lådan inte rör sig. Här är F_g tyngden av lådan, N är normalkraften på lådan och F_f är friktionskraften som gör att lådan inte glider nedför underlaget. Dessa krafter pekar åt lite olika håll. Sedan behöver man veta att man kan dela upp en kraft i komposanter. Dessa komposanter har samma verkan på lådan som den ursprungliga kraften. Vi väljer 2 riktningar som vi kallar x och y och delar upp alla krafter i komposanter som pekar i x- och y-led. NI innebär att summan av krafterna i x-led måste vara 0. Annars hade lådan börjat röra sig i x-led. Detsamma gäller för y-led. Alltså inför vi ett koordinatsystem. Man kan välja vilka riktningar som helst. I det här fallet så ser vi i figuren att vi kan välja x- och y-riktningar så att vi slipper dela upp F_f och N i komposanter.

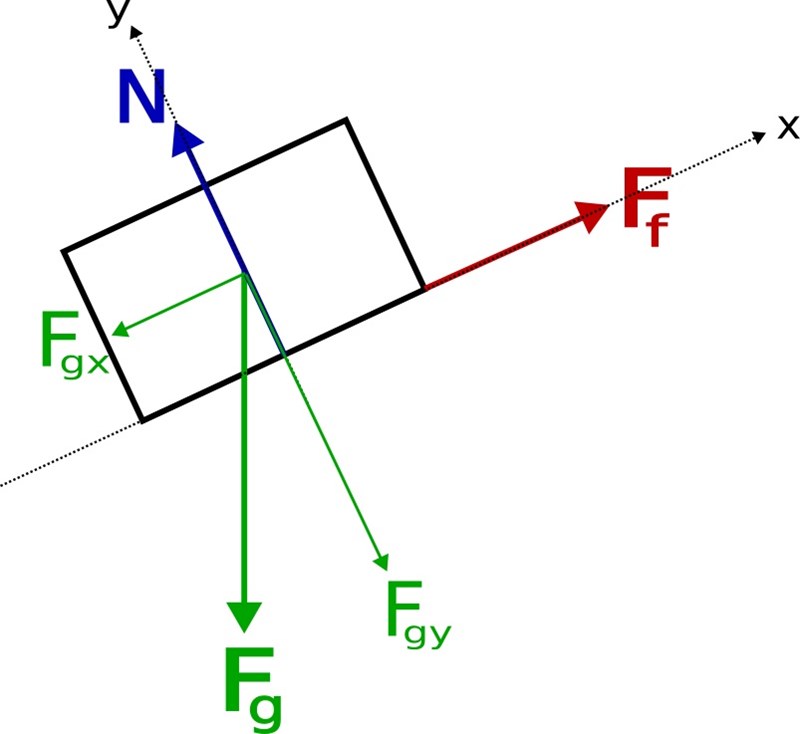
Här ser vi att N bara har en y-komposant och F_f bara har en x-komposant. Vi behöver bara dela upp F_g i komposanter. Det är ren matematik/geometri/trionometri.

sin 32 = F_gx/F_g
cos 32 = F_gy/F_g

D.v.s.

F_gx = F_g sin 32           (1)
F_gy = F_g cos 32          (2)

Nu kommer vi tillbaka till fysiken, för när det står att vi ska anta att 32$°$ är jämviktspunkten så menar man att friktionskraften når sitt maximum vid 32$°$ (friktionskraften varierar och den är t.ex. 0 om lutningen hade varit 0 grader). Det är därför lådan börjar glida då. Friktionen kan inte hålla emot F_gx längre och lådan börjar glida. Hade friktionen kunnat bli ännu större så hade lådan legat stilla även vid 33$°$ och kanske t.o.m. vid 40$°$. Nu måste vi veta hur friktion fungerar och du har säket sett denna:

F_f = $\mu$ N                      (3)

där $\mu$ är friktionskoefficienten. F_f i den formeln är den maximala friktionskraften. Om vi tillämpar NI i x-led så ser vi i figuren att F_f = F_gx (annars hade lådan börjat röra sig i x-led, glida längs underlaget). Då kan vi skriva om ekvation 1 så här:

F_f = F_g sin 32

Nu börjar det bli dags att kolla vilken information som vi har fått i uppgiften. I uppgiften står det vad F_f är, F_f = 250 N. D.v.s.

250 = F_g sin 32

Om vi sedan tillämpar NI i y-led så ser vi att N = F_gy (annars hade lådan börjat röra sig i y-led, antingen sväva iväg eller rasa genom underlaget). Då kan vi skriva om ekvation 2 så här:

N = F_g cos 32

och då är det en smal sak att beräkna $\mu$ med ekvation 3.