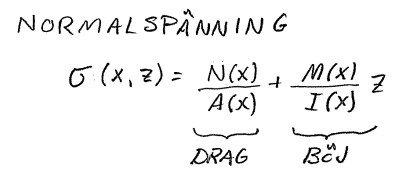Hållfasthetslära: böjmoment, krökningsradie, fel i facit

Hej, här är frågan:

Samt facit:

Kappa i deras ledtråd är ju i själva verket bara en omskrivning av detta (N=0, och dela båda led med E(z)):

Och det de alltså har i integranden är:

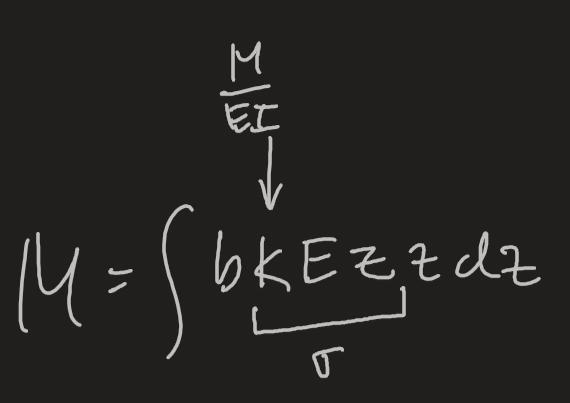
Kan de verkligen bryta ut kappa ur alla integraler när den beror av E(z) som är z-beroende? Och dessutom ska E(z) ta ut varandra, och hela deras arugment borde resultera i $-\frac{PL}{4}=-\frac{PL}{4}$ . Jag blir frustrerad eftersom jag försökte med en liknande lösning men visste inte hur jag skulle få in E nånstans i uttrycket.

Krökningen beror inte på varken $z$ eller $x$ utan är en konstant som beskriver krökningsradien $\rho = 1/\kappa$ för neutralplanet i balken. Från neutralplanet antar man sedan att spänningen ökar linjärt. Det är fritt fram att bryta ut $\kappa$ ur integralen.

Om du tittar på deras resultat ser du att det man kunnat använda sig av är närmast en form av effektiv styvhet:

$E* = \dfrac{15}{16}E$

Det finns metoder för att räkna ut denna för sandwich-balkar vilket direkt hade gett krökningen från:

$\kappa = \dfrac{M_b}{E* I}$

Normalt använder man sig dock av en slags referens-area(styvhet) och ett referens-areamoment. Det går att läsa om detta på Wikipedia. Då får man alltså:

$\kappa= \dfrac{M_b}{E_{ref}I_{ref}}$

Tillägg: 30 maj 2023 11:28

Lite fel, fixar nedan senare Nu äntligen rätt

Wikipedia var grötigt beskrivet men ovan beräknas enligt:

$E_{ref} = \dfrac{E_i}{n_i}, i =1,2,3,...$

Här väljs alltså referens-styvhet godtyckligt. I detta fall skulle alltså vi ha tre olika sektioner och $i =1,2,3$ där vi väljer $E_{ref} = E$ och får:

$n_1 = 1$ , $n_2 = 1/2$ , $n_3 =1$

Där alltså ytterskikt är $i =1,3$ och kärna är $i =2$ .

Du får också:

$\displaystyle I_{ref} = \sum_{i=1}^3 n_i I_{A_i}$

Här beräknas alltså $I_{A_i}$ som areamoment relativt neutrallagret vilket på grund av symmetri är i mitten av tvärsnittet. Vi skulle alltså med hjälp av Steiners sats få:

$I_{ref} = 2(1\cdot (\dfrac{b(h/4)^3}{12}+\dfrac{bh}{4}\cdot (\dfrac{3h}{8})^2))+1/2\cdot (\dfrac{b(h/2)^3}{12}+\dfrac{bh}{2}\cdot 0^2)$

Vi får:

$I_{ref} = \dfrac{5bh^3}{64}$

Detta ger slutligen:

$\kappa=\dfrac{M_b}{E_{ref}I_{ref}}=-\dfrac{PL/4}{E\cdot \dfrac{5bh^3}{64}}$

Det är alltså olika E:n på spel här, men vad betyder "effektiv" styvhet? Genomsnittlig styvhet borde ju bara 0.75E?

Qetsiyah skrev:
Det är alltså olika E:n på spel här, men vad betyder "effektiv" styvhet? Genomsnittlig styvhet borde ju bara 0.75E?

Effektiv styvhet är som ett mått på styvheten viktad med dess geometri och statiska moment. Men, det är enklare med standardsättet att räkna på. Kolla mitt föregående inlägg under spoiler för ett nu korrekt uppdaterat tillvägagångssätt.

Svara Avbryt

Visa senaste svar