Har jag resonerat korrekt?
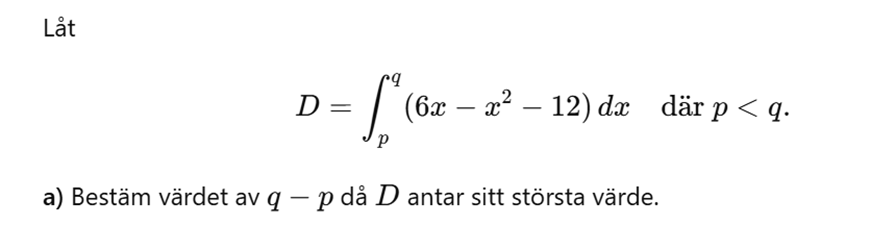

Är det korrekt att svara med ett gränsvärde för a, eller skall jag svara q-p = 0?
Angående b, finns det en lösning här som jag har missat? 
Varför skulle 0 vara D:s största värdet?
Det finns olika sätt man kan lösa detta på. Du är på rätt väg när du funderar över positiva och negativa bidrag till integralens värde ("positiv/negativ area"). Jag kan ge dig två tips:
1, p och q är integralgränserna. Det borde vara så att gränserna när funktionen befinner sig maximalt ovanför x-axeln ger den största positiva arean och således största värdet på D:
2, Tänk nollställen.
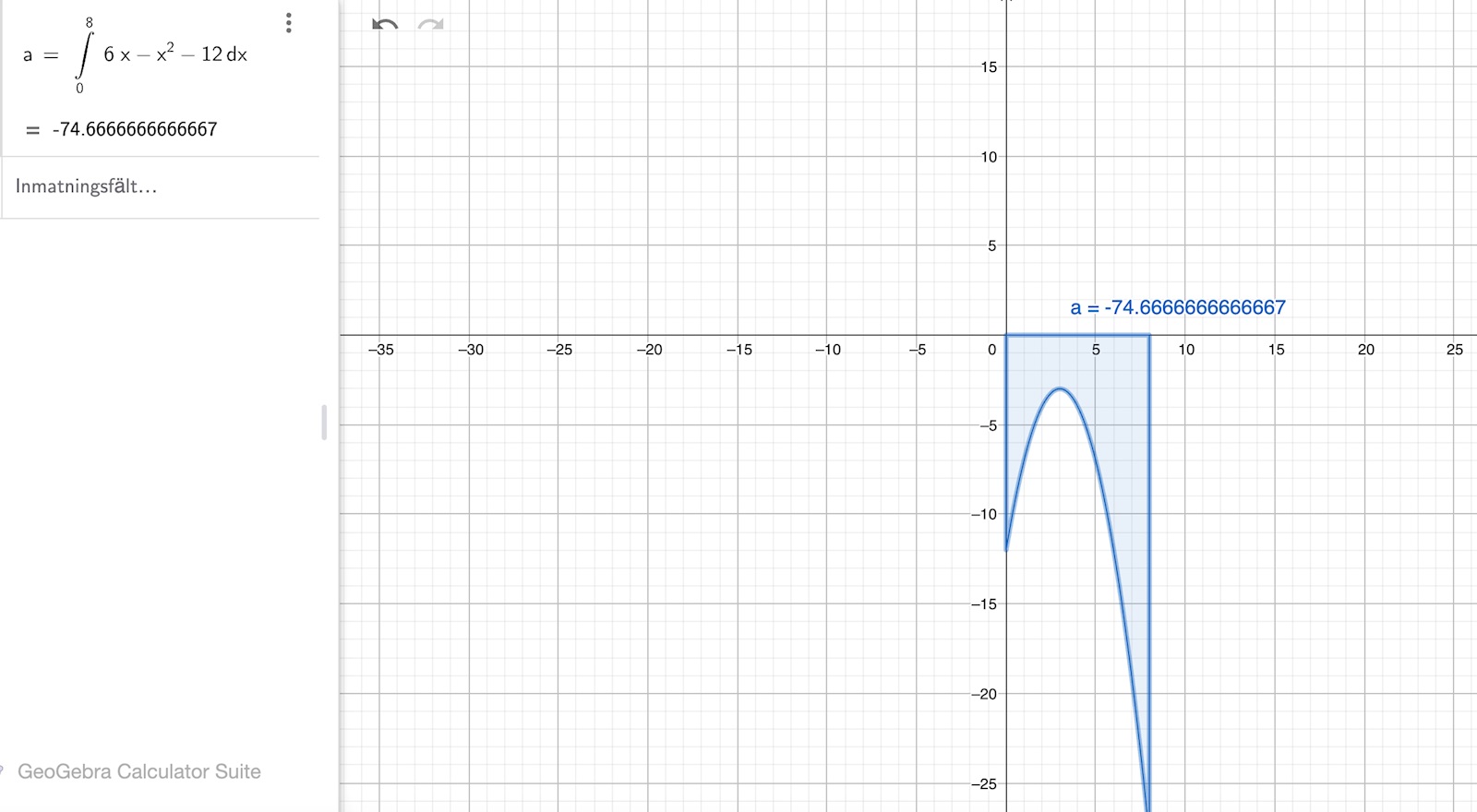
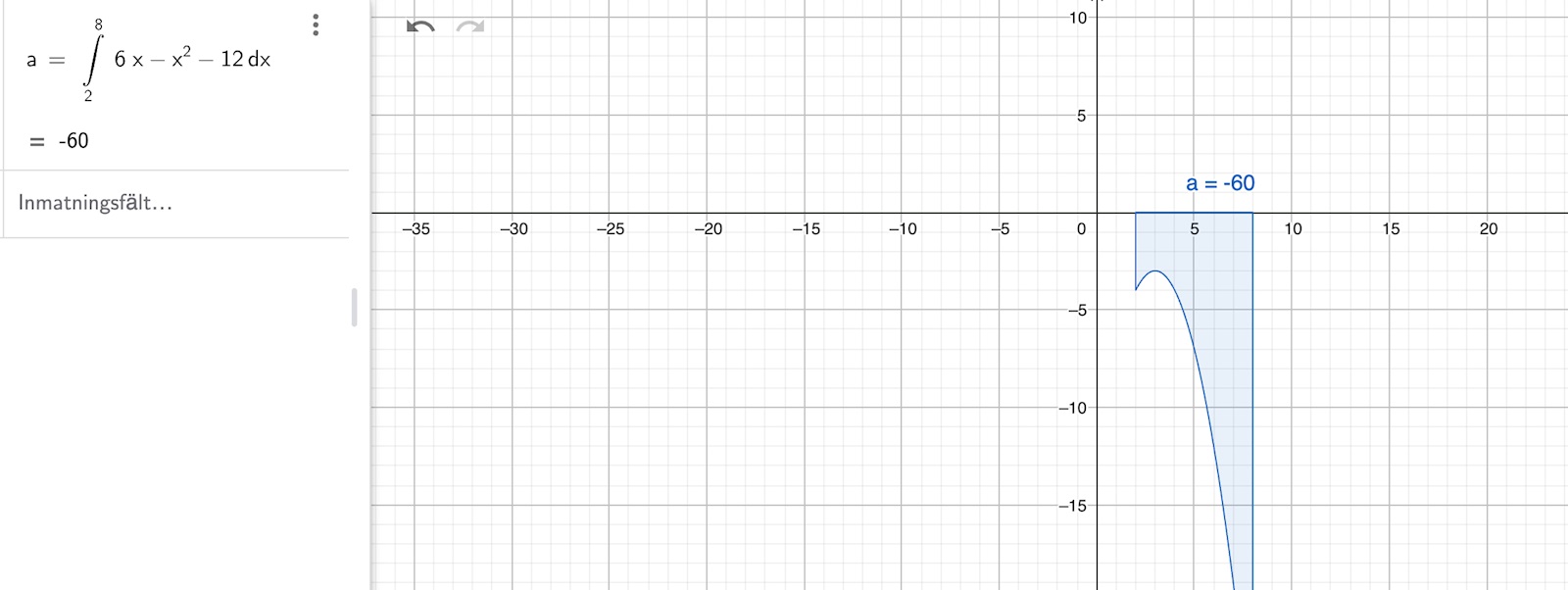
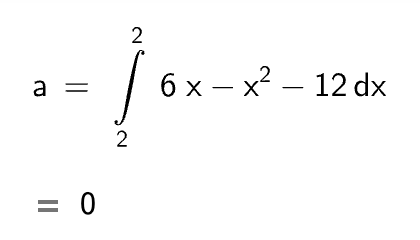 När jag stoppar in integralen i GeoGebra ser det ut som att det enda sättet att få ett positivt värde på D är att sätta första intervallvärdet som större än det andra, alltså q<p vilket inte tillåts av uppgiften. Annars verkar alla integralgränser ge ett negativt värde. Om p och q har samma värde borde ju D få ett värde som är noll. 0 är ju större än ett negativt värde, därför borde D=0 bli största värde enligt min beräkning och av det som visas av grafen ovan.
När jag stoppar in integralen i GeoGebra ser det ut som att det enda sättet att få ett positivt värde på D är att sätta första intervallvärdet som större än det andra, alltså q<p vilket inte tillåts av uppgiften. Annars verkar alla integralgränser ge ett negativt värde. Om p och q har samma värde borde ju D få ett värde som är noll. 0 är ju större än ett negativt värde, därför borde D=0 bli största värde enligt min beräkning och av det som visas av grafen ovan.
Det verkar som att om man inverterar integralgränserna så blir det positivt som nämnt ovan, men det tillåts inte eftersom q måste vara större än p.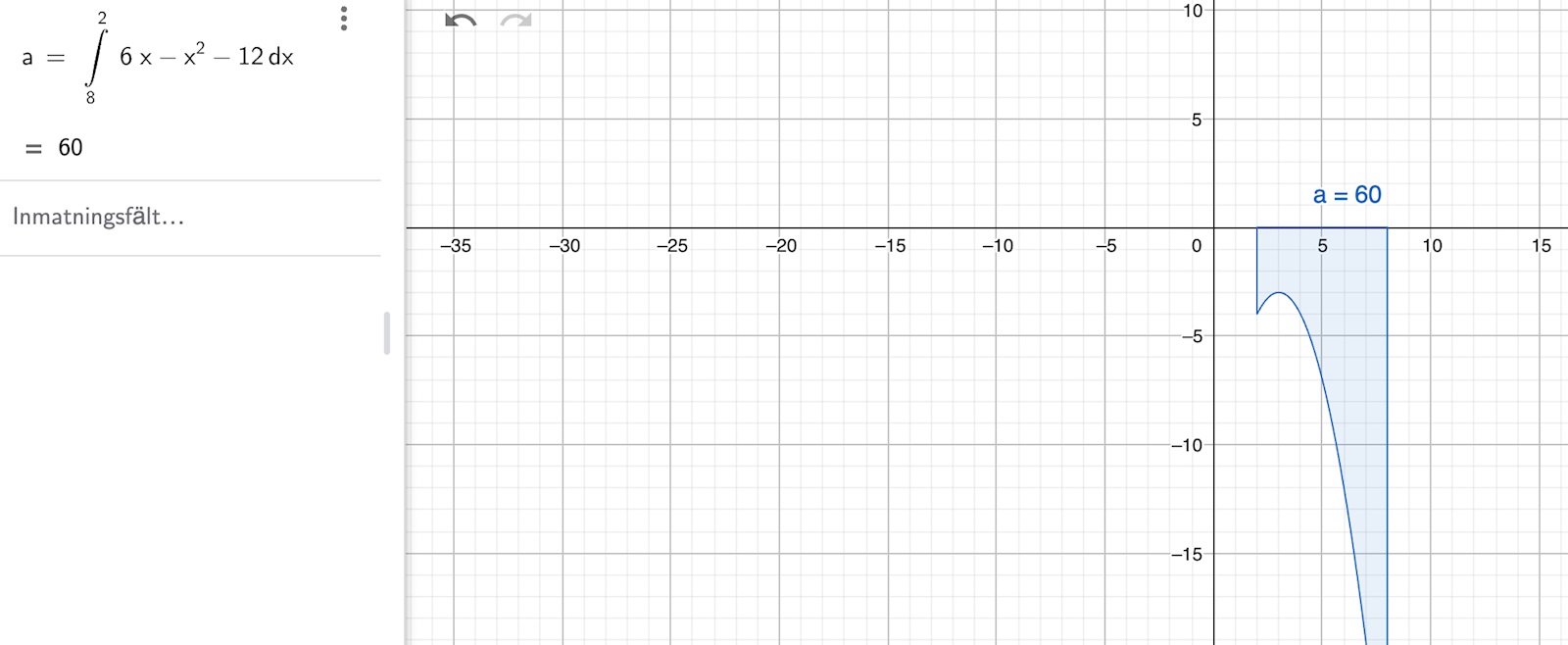
Jag skulle nog gissa att det är fel i uppgiften.
Ditt resonemang är OK. Integralens värde kan aldrig bli positivt, så ger det största värdet på , nämligen , varför i (a)-uppgiften.
I (b)-uppgiften finns det inget sådant intervall , så det finns inget största värde på .
Edit: Nu har jag märkt att man kräver att , så man kan inte välja , så värdet kommer aldrig antas. Därmed finns det inte heller något svar i (a)-uppgiften
Tack för svar, så jag bör svara q-p = 0 istället för ett gränsvärde för a?
Att skriva att det inte finns en lösning för b borde väl räcka?
När du skriver att mitt resonemang är OK, vad menar du det är som kan förbättras?
Jag redigerade mitt svar i #4 efter att du svarat. Eftersom krävs (d.v.s. inte ), så finns det inte heller något svar i (a)-uppgiften, då det inte finns något största värde på .
Jag råkade skriva in +12 i Desmos… men då tycker jag uppgiften blir bättre!😃
Ok, men varför kan man inte använda ett gränsvärde för att beskriva a? Jag förstår inte varför det inte går. Eller är det möjligt?
Uppgiften frågar om värdet på något uttryck ifall är som störst. Talet kan komma hur nära som helst till , men kommer aldrig nå den.
Villkoret "ifall är som störst" är därmed aldrig uppfyllt. Då är det meningslöst att fråga om värdet på under det villkoret eftersom aldrig är lika med sitt största värde.
Ok, så det går att beskriva med gränsvärde men det är ingenting som efterfrågas i uppgiften? Har jag förstått det rätt då?
Exakt

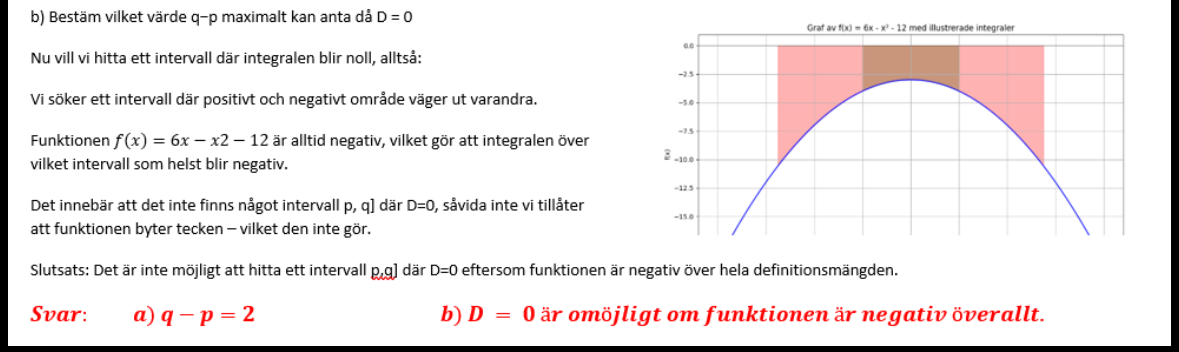
Jag fick fel på a. Kan någon förklara lösningen för a, jag förstår inte riktigt. Jag trodde en lösning på a inte var möjlig?
De ger ett exempel (4-2=2) som ett allmängiltigt svar i a. Enligt resonemanget i svaret borde väl värdena lika gärna kunna vara p=2.5 och q=3.5 eller p=2.6 och q=3.4. Här borde väl man se att q-p går mot noll? Alltså som ett gränsvärde? Vad är det jag inte förstår?
Varifrån kommer detta? Det är ju nonsens. Kan det handla om en dålig översättning / missbruk av begreppet "största värde"?
Det var en spännande lösning. Tänkte att hen trodde att integralgränserna bara kunde vara heltal, men pga ”exempelvis” tror jag inte examinatorn förstår frågan alls.


