Harmonisk svängning
Hej! Behöver hjälp med denna fråga. Vet att det finns liknande trådar. Har läst dessa, men där deriverar man inte, och som jag förstår av uppgiften så vill dem att man ska derivera.
Frågan är: En partikel med massan 350 g utför en harmonisk svängning med amplituden 0,15 m kring ett
jämviktsläge. Svängningstiden är 1,5 s.
a) Hur stor är den resulterande kraften på partikeln i det ögonblick då avståndet från jämviktsläget är 0,10 m? Ledtråd: Derivera elongationen för att få hastigheten. Derivera hastigheten för att få accelerationen.
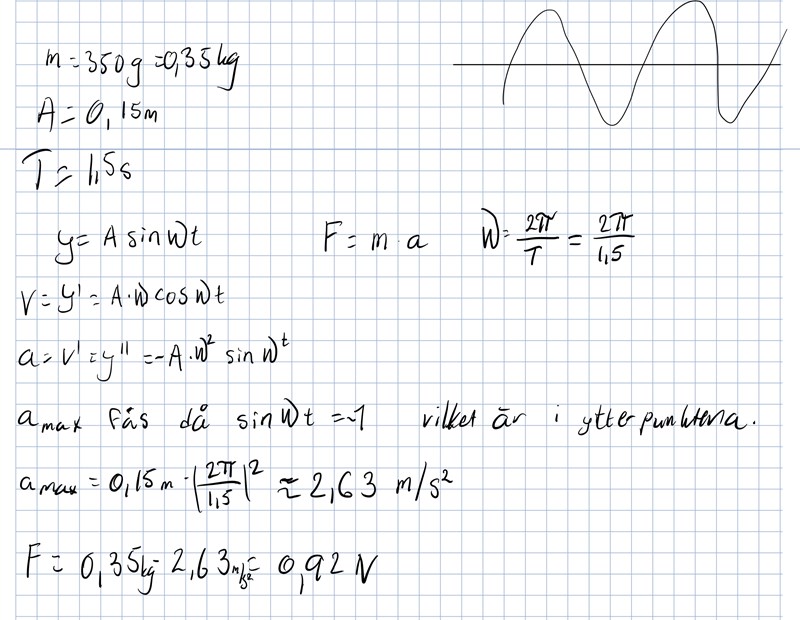
Har räknat ut vad amax är men vet inte hur jag ska komma fram till vad kraften är 0,10 m från jämnvikten...
Hur ska jag komma vidare?
Hjälp! skrev:Hej! Behöver hjälp med denna fråga. Vet att det finns liknande trådar. Har läst dessa, men där deriverar man inte, och som jag förstår av uppgiften så vill dem att man ska derivera.
Frågan är: En partikel med massan 350 g utför en harmonisk svängning med amplituden 0,15 m kring ett
jämviktsläge. Svängningstiden är 1,5 s.
a) Hur stor är den resulterande kraften på partikeln i det ögonblick då avståndet från jämviktsläget är 0,10 m? Ledtråd: Derivera elongationen för att få hastigheten. Derivera hastigheten för att få accelerationen.
Har räknat ut vad amax är men vet inte hur jag ska komma fram till vad kraften är 0,10 m från jämnvikten...
Hur ska jag komma vidare?
Beräkna vid vilket värde på t som elongationen är 0,1. Sätt in det värdet i ekv för acceketationen eftersom F=ma kan du sedan brr kraften
Hej!
Samma person, men det andra kontot strular...
Får svaret -0,0067N, blir osäker om det verkligen kan stämma då jag tycker det känns som en oerhört liten kraft..
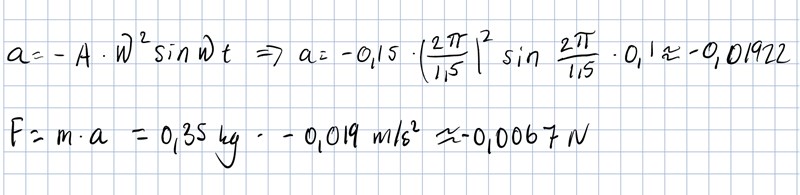
Det är inte tiden som är 0,1 utan avståndet från jämviktsläget. Dvs
Asin() = 0,1. Jämför detta med formeln för accelerationen, som också har en faktor Asin().
Okej, tack!
Har räknat om och får nu svaret - 0,61N vilket verkar betydligt rimligare. Vill bara dubbelkolla så att jag fattat det rätt nu.
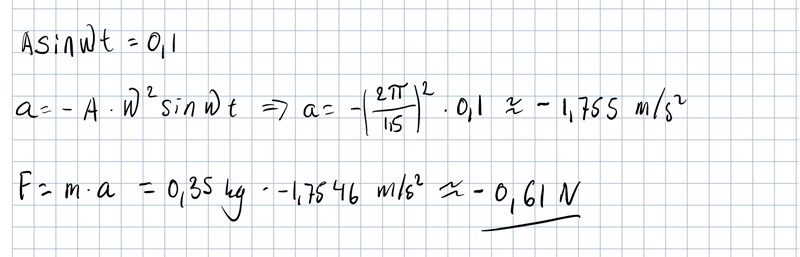
Fysikproblem skrev:Okej, tack!
Har räknat om och får nu svaret - 0,61N vilket verkar betydligt rimligare. Vill bara dubbelkolla så att jag fattat det rätt nu.
Ja, du har fattat rätt.


