Harmonisk svängning
 jag behövde ha hjälp med att komma igång för uppgift 9 och 10
jag behövde ha hjälp med att komma igång för uppgift 9 och 10
9) Periodtiden beror av massan och fjäderkonstanten. Hur ser uttrycket ut?
Dr. G skrev:9) Periodtiden beror av massan och fjäderkonstanten. Hur ser uttrycket ut?
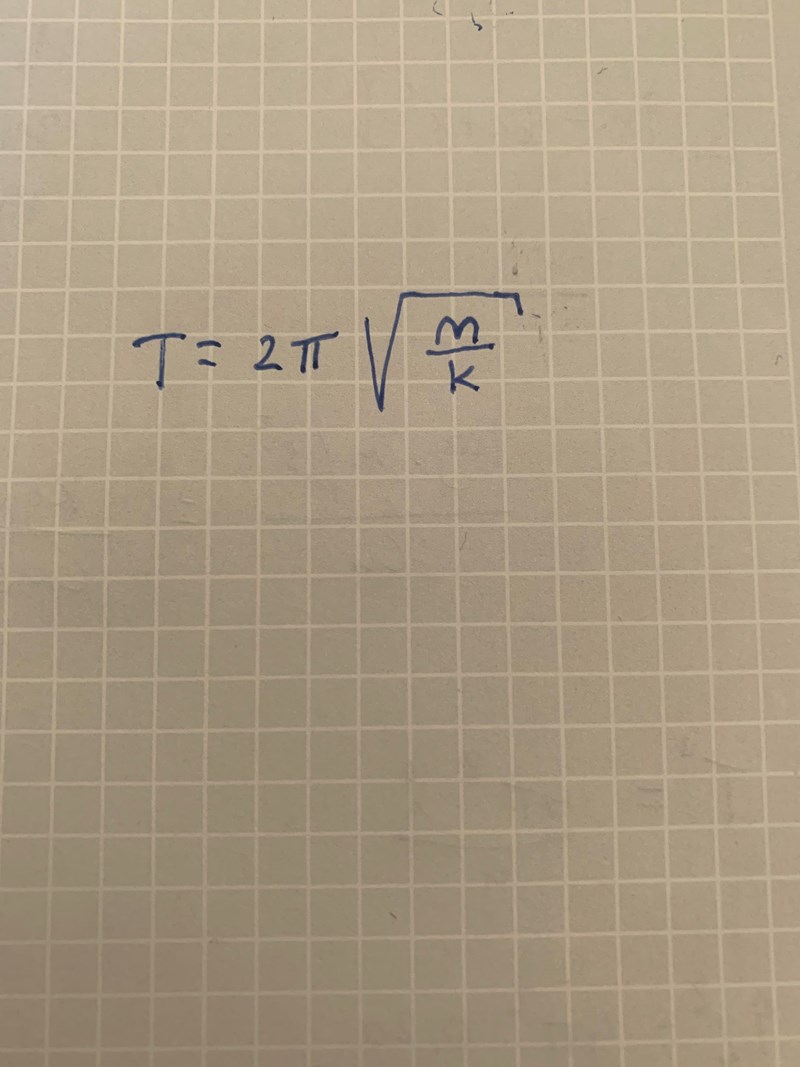
Ja.
Vad blir då log(T) uttryckt i log(m)?
Dr. G skrev:Ja.
Vad blir då log(T) uttryckt i log(m)?
Ska jag logaritmera bägge sidor?
Ja
Dr. G skrev:Ja
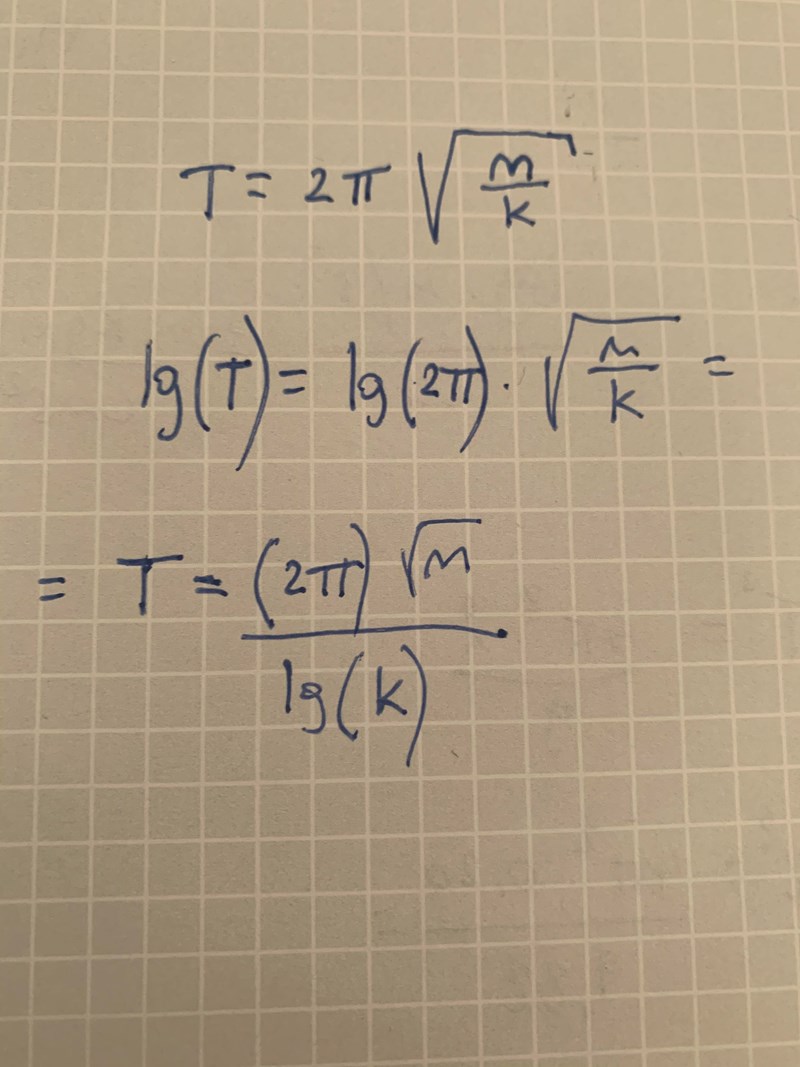 sådär kanske?
sådär kanske?
Nej, du måste använda logaritlagarna för produkt och exponent.
Kanske blir det lättare om båda led först kvadreras och sedan logaritmeras.
Dr. G skrev:Nej, du måste använda logaritlagarna för produkt och exponent.
Kanske blir det lättare om båda led först kvadreras och sedan logaritmeras.
Vet inte hur jag ska göra..
Är du med på att
och att
(för a > 0, b > 0)
?
Dr. G skrev:Är du med på att
och att
(för a > 0, b > 0)
?
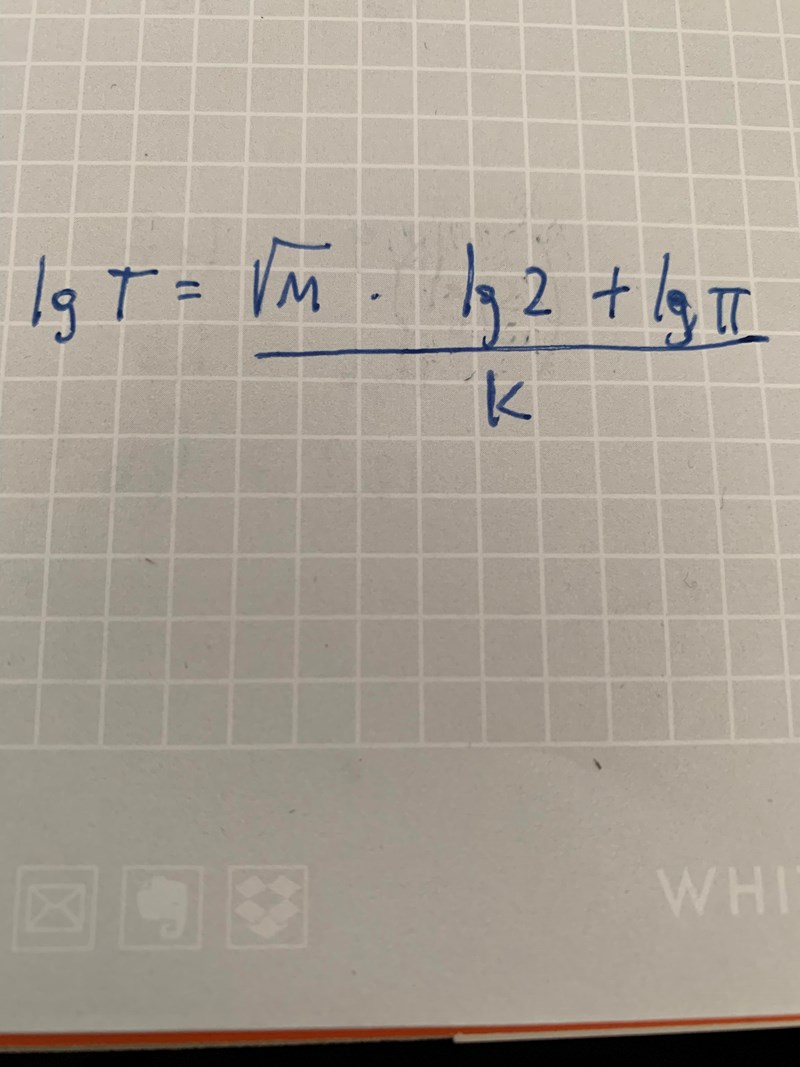
Det blir lite lättare (man slipper bråk) om man först kvadrerar:
logaritmera:
Nu kan man använda logaritmlagar. Du vill få ut log(T) som funktion av log(m).
Är något steg hittills oklart?
Dr. G skrev:Det blir lite lättare (man slipper bråk) om man först kvadrerar:
logaritmera:
Nu kan man använda logaritmlagar. Du vill få ut log(T) som funktion av log(m).
Är något steg hittills oklart?
Ja jag är med, jag tänkte Logaritmera direkt på detta vis:
T=2*pi*(m/k)^0.5
Logaritmering ger:
lnT=ln2+ln(pi) +0.5*(lnm-lnk)
Sedan står det att jag ska forma en linjär funktion mellan ln(T) och ln(m), jag tänker på då y=kx+m
T^2=Km
T^2=Km
som kan
jämföras med
T2=(2π)^2k*m
Sen är det stopp
Alfredo skrev:Logaritmering ger:
lnT=ln2+ln(pi) +0.5*(lnm-lnk)
Här är du nästan klar.
Förenkla till
(Bytte sedvanliga k och m till b och a, eftersom k och m här betyder fjäderkonstant respektive massa.)
Dr. G skrev:Alfredo skrev:Logaritmering ger:
lnT=ln2+ln(pi) +0.5*(lnm-lnk)Här är du nästan klar.
Förenkla till
(Bytte sedvanliga k och m till b och a, eftersom k och m här betyder fjäderkonstant respektive massa.)
Hur då förenkla?
Kanske inte förenkla, men uttryck a och b i kända storheter.
b = 1/2
a = ...
Dr. G skrev:Kanske inte förenkla, men uttryck a och b i kända storheter.
b = 1/2
a = ...
ln2+lnpi=ln2pi. Detta värde beräknade jag till 1,838.
lnT=0,5lnm+1,838-0,5lnk
Jag hade nog lämnat det som
men du får samma sak, ifall du använder ln.
Dr. G skrev:Jag hade nog lämnat det som
men du får samma sak, ifall du använder ln.
Jag har gjort 10an, men vet inte hur jag ska plotta det i excel..
Lägg in m och T i olika kolumner.
Skapa nya kolumner som är ln(m) och in(T).
Dr. G skrev:
Lägg in m och T i olika kolumner.
Skapa nya kolumner som är ln(m) och in(T).
är det så du menar?


