Harmoniskt Svängningsrörelse i vätska

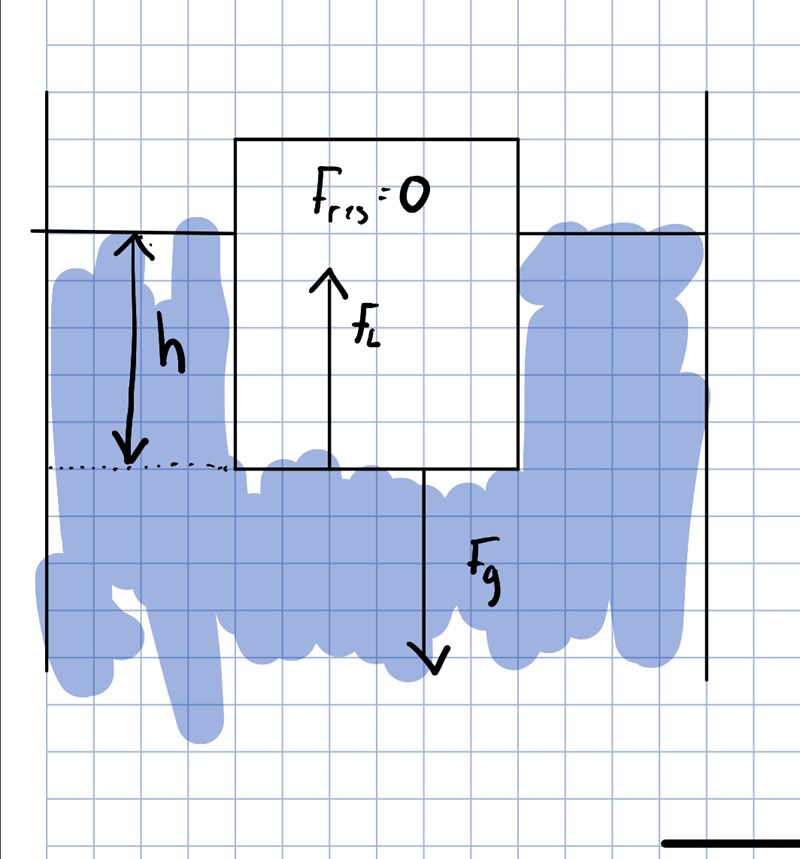
Jag sitter nu fast på denna fråga då jag är inte säker på vart man ska börja. Jag kan observera att det finns en tyngdkraft som verkar på kuben och en återförande kraft från vätskan som är riktat uppåt som om det vore en fjäder.
Så om det är kraftjämfikt så råder det följande,
pv=?
Fv-Fg=0
Fg=mg
P= pvgh
Fv=A * P = A *pgh
A * pvgh - mg = 0
Därefter har vi perioden, och kan få ut en vinkelhastighet
Men nu vet jag inte hur jag ska ta mig vidare i uppgiften.
Ytterligare har trädet en densitet, och en höjd.
pträ=m/v
men för att dem endast ger oss en höjd kan jag inte få ut massan då det krävs en radie från cylindern.
Mattezel skrev:men för att dem endast ger oss en höjd kan jag inte få ut massan då det krävs en radie från cylindern.
Det är väl tänkt att det ska vara oberoende av radie.
Problemet är inte realistiskt. Det finns en enorm dämpning. Och det är inte bara korkens massans tröghet som är viktig. Det är ju också en hel del vätska som skvalpar fram och tillbaka.
Varifrån kommer uppgiften?
Pieter Kuiper skrev:Mattezel skrev:men för att dem endast ger oss en höjd kan jag inte få ut massan då det krävs en radie från cylindern.
Det är väl tänkt att det ska vara oberoende av radie.
Problemet är inte realistiskt. Det finns en enorm dämpning. Och det är inte bara korkens massans tröghet som är viktig. Det är ju också en hel del vätska som skvalpar fram och tillbaka.
Jag antar att dem har försummat hur vätskans kommer bete sig. Och att man ska på något sätt se att dämpningen kommer alltid rikta sig mot kraftjämvikten. T.ex. När korken är på väg ner mot djupet kommer kraften från vätsketrycket att öka. och den resulterande kraften ger en dämpning mot rörelseriktningen.
Smaragdalena skrev:Varifrån kommer uppgiften?
En gammal ex tenta från fysik 2
Mattezel skrev:Pieter Kuiper skrev:Mattezel skrev:men för att dem endast ger oss en höjd kan jag inte få ut massan då det krävs en radie från cylindern.
Det är väl tänkt att det ska vara oberoende av radie.
Problemet är inte realistiskt. Det finns en enorm dämpning. Och det är inte bara korkens massans tröghet som är viktig. Det är ju också en hel del vätska som skvalpar fram och tillbaka.Jag antar att dem har försummat hur vätskans kommer bete sig. Och att man ska på något sätt se att dämpningen kommer alltid rikta sig mot kraftjämvikten. T.ex. När korken är på väg ner mot djupet kommer kraften från vätsketrycket att öka. och den resulterande kraften ger en dämpning mot rörelseriktningen.
Det är inte vad dämpning är. Dämpning gör att energin går förlorad i vattnets rörelser. Och den är stark, amplituden går snabbt ner. Lätt att testa med sin badanka :)
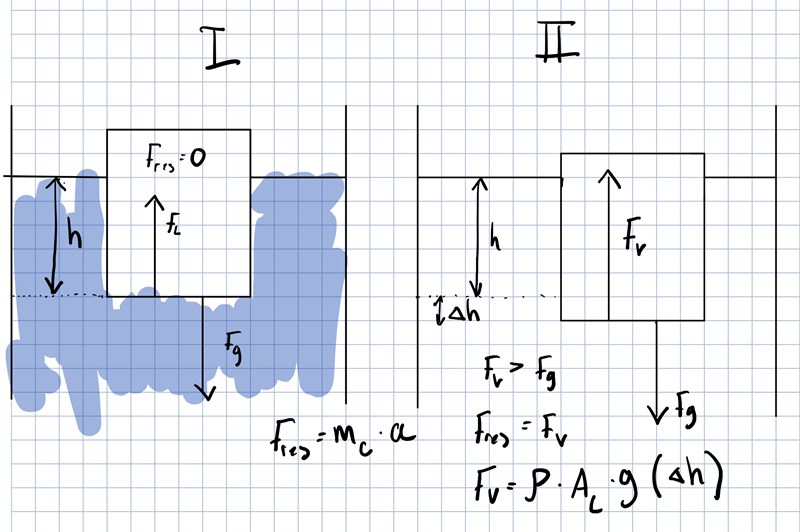
Tanken är att du ska räkna ut någon typ av "fjäderkonstant" som i Hookes lag. Och bestämma .
Pieter Kuiper skrev:Mattezel skrev:Pieter Kuiper skrev:Mattezel skrev:men för att dem endast ger oss en höjd kan jag inte få ut massan då det krävs en radie från cylindern.
Det är väl tänkt att det ska vara oberoende av radie.
Problemet är inte realistiskt. Det finns en enorm dämpning. Och det är inte bara korkens massans tröghet som är viktig. Det är ju också en hel del vätska som skvalpar fram och tillbaka.Jag antar att dem har försummat hur vätskans kommer bete sig. Och att man ska på något sätt se att dämpningen kommer alltid rikta sig mot kraftjämvikten. T.ex. När korken är på väg ner mot djupet kommer kraften från vätsketrycket att öka. och den resulterande kraften ger en dämpning mot rörelseriktningen.
Det är inte vad dämpning är. Dämpning gör att energin går förlorad i vattnets rörelser. Och den är stark, amplituden går snabbt ner. Lätt att testa med sin badanka :)
Tanken är att du ska räkna ut någon typ av "fjäderkonstant" som i Hookes lag. Och bestämma .
Försöker uppgiften säga att det finns någon sorts korrelation att vattnet beter sig som en fjäder på denna kork?
Men om vi använder
introducerar vi inte bara 2 extra okända variabler? Då nu måste vi hitta vattnets "hypotetiska" k och vattnets massa.
Mattezel skrev:
Försöker uppgiften säga att det finns någon sorts korrelation att vattnet beter sig som en fjäder på denna kork?
Ja. Kraften är proportionell mot avvikelsen från jämviktsläget, precis som i Hookes lag.
Tanken är nog att man ska använda träbitens massa. Men det är ingen realistisk approximation, tycker jag.
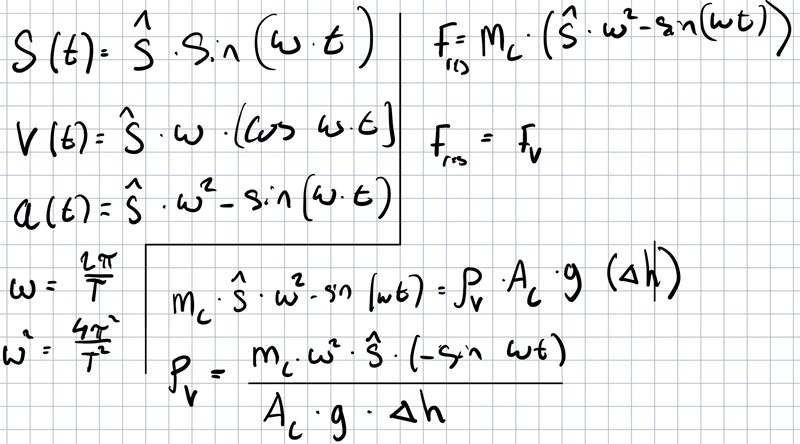 Ser inte ut som jag kommer vidare.Då det fortfarande är 4 okända.
Ser inte ut som jag kommer vidare.Då det fortfarande är 4 okända.
Mattezel skrev:Ser inte ut som jag kommer vidare.Då det fortfarande är 4 okända.
Du vet perioden, du vet specifik massa, hur stor är då kraftkonstanten?
Pieter Kuiper skrev:Mattezel skrev:Ser inte ut som jag kommer vidare.Då det fortfarande är 4 okända.
Du vet perioden, du vet massa, hur stor är då kraftkonstanten?
Jag har inte massan av cylindret, men jag kan ersätta den med densiteten x cylindrets volym.
Delta h borde vara lika med amplituden x sin wt. Då utesluter det endast Cylindrets area på nämnaren och cylindrets volym på täljaren
Du vet perioden, så du kan bestämma m/k.
Du vet specifik massa. Massa är proportionell mot area.
Kraftkonstanten är också proportionell mot area.
I den här förenklade modellen räcker det för att bestämma vätskans densitet.
Pieter Kuiper skrev:Du vet perioden, så du kan bestämma m/k.
Du vet specifik massa. Massa är proportionell mot area.
Kraftkonstanten är också proportionell mot area.I den här förenklade modellen räcker det för att bestämma vätskans densitet.
Förlåt, men jag har lite svårt att förstå. Massan är väl proportionell mot volymen? Vilket vi inte vet. Vi vet inte heller arean, utan vi vet endast längden på denna cylinder.
Uppgiften är nog för svår för gymnasiet.
Pieter Kuiper skrev:Uppgiften är nog för svår för gymnasiet.
Så om vätskans densitet stämmer överens bör det vara glykol. Misstaget jag gjorde var att inte förlänga bråket med höjden av cylindret så att göra om arean i nämnaren till volymen.