Hästhage
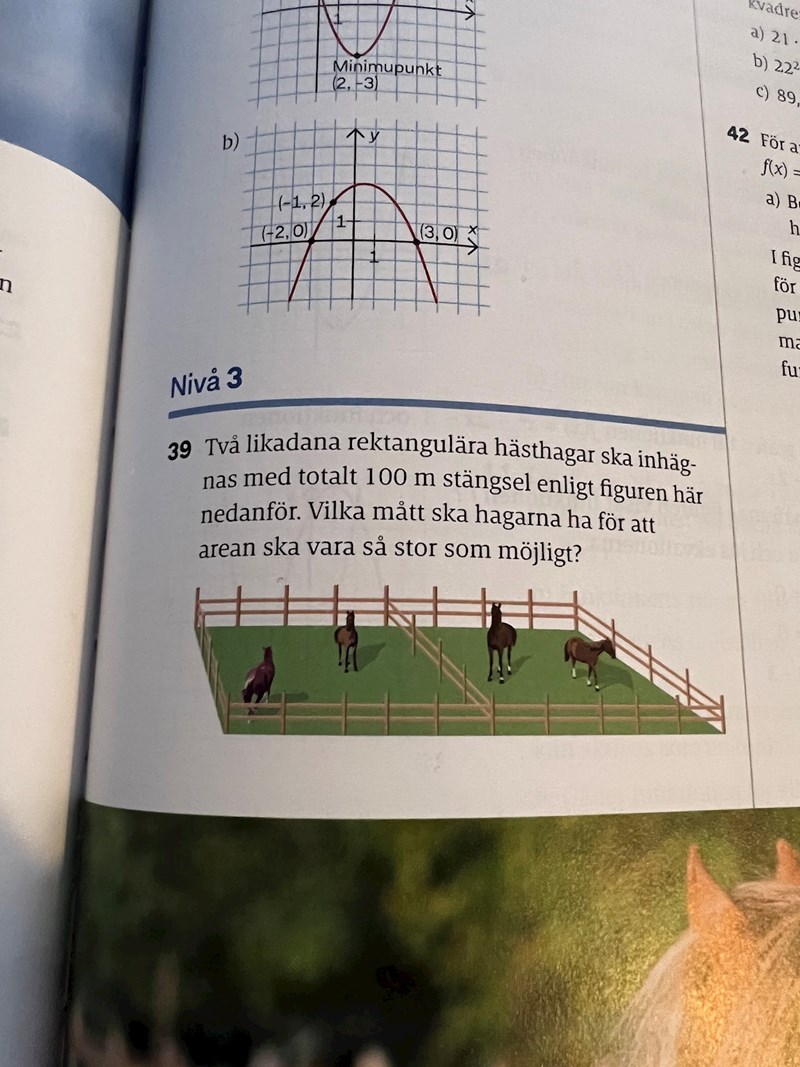
Två likadana rektangulära hästhagar ska inhägnas med totalt 100 meter stängsel. Vilken mått ska hagarna ha för att arean ska vara så som möjligt?
Jag vet inte hur jag ska börja.
Uppgiften går att tolka på flera olika sätt.
Kan du ladda upp en bild på den?
OK bra, då är det entydigt.
Sätt x = längden av vänstra, mittersta och högra stängslet.
Sätt y = längden av främre vänstra, främre högra, bakre vänstra och bakre högra stängslet.
Det finns alltså 3 stängsel av längden x och 4 stängsel av längden y.
Sätt nu upp ett uttryck för hagarnas sammanlagda area och en ekvation för den totala stängsellängden.
Du ska nu försöka hitta de värden på x och y som gör den sammanlagda arean så stor som möjligt.
Visa dina försök.
Yngve skrev:OK bra, då är det entydigt.
Sätt x = längden av vänstra, mittersta och högra stängslet.
Sätt y = längden av främre vänstra, främre högra, bakre vänstra och bakre högra stängslet.
Det finns alltså 3 stängsel av längden x och 4 stängsel av längden y.
Sätt nu upp ett uttryck för hagarnas sammanlagda area och en ekvation för den totala stängsellängden.
Visa dina försök.
3x + 4y= 100
2y*x = sammanlagd area
Jag vet inte hur jag ska fortsätta
Vill du arean ska vara så stort eller så liten som möjligt? Det ska vara tydlig
Amir123 skrev:
3x + 4y= 100
2y*x = sammanlagd area
Jag vet inte hur jag ska fortsätta
Bra, det är rätt.
Lös ut y ut den första ekvationen och använd detta för att ersätta y i uttrycket för arean.
Då får du ett uttryck för arean som endast beror av x och du kan använda dina kunskaper om andragradsfunktioner för att bestämma det största värdet.