Hastighet

Jag är inte helt säker på att jag förstår din fråga. Den är inte superlätt att läsa, men jag gör ett försök.

I bilden visas ett v-t-diagram. Man håller konstant hastighet under en timme.

Du vet säkert att s = vt, så om man kör 70 km per timme och kör i en timme, så är sträckan:
s = 70 km/h * 1 h = 70 km

Det är också arean av den streckade rektangeln i bilden. Rektangelns area är ju basen (=1) * höjden (=70).

Om y-axeln är i enheten km/h och x-axeln i enheten h, så blir ju km/h * h = enheten km.

Det där med att beräkna arean har med primitiva funktioner och integraler att göra, men det är nog kanske en bit fram i gymnasiekursen. 

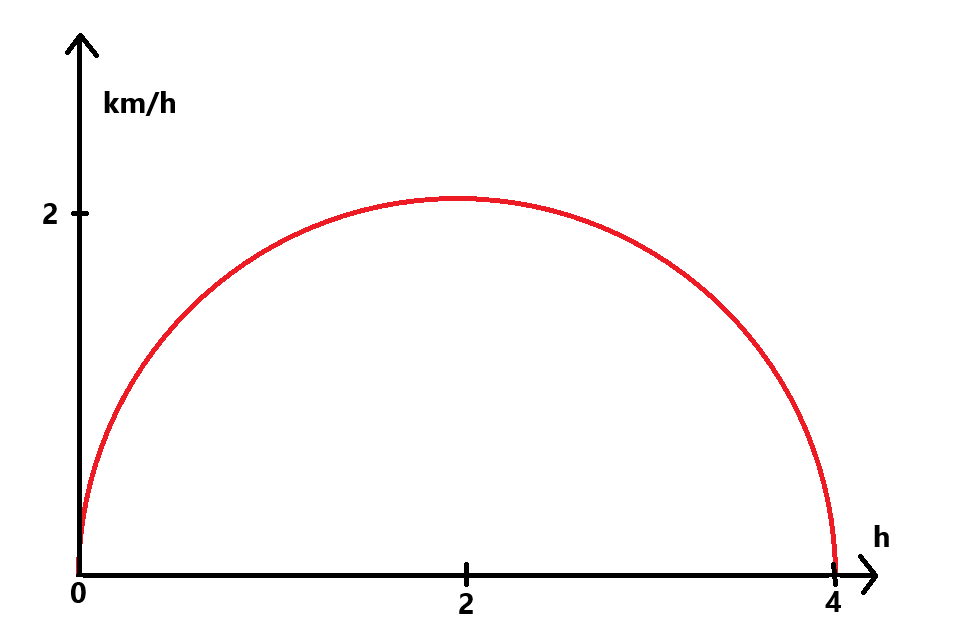
Tänk dig detta v-t-diagram istället:

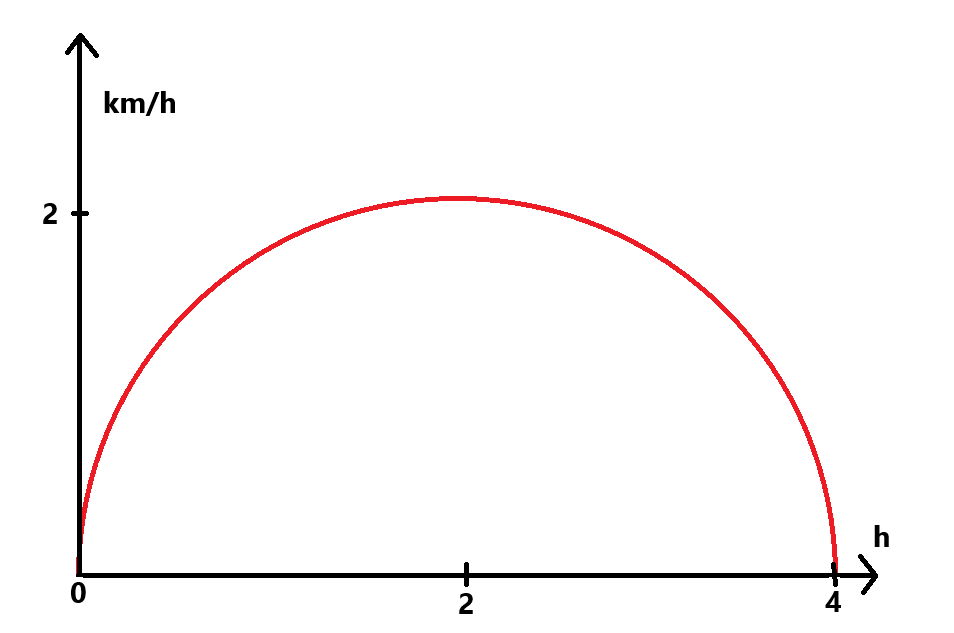
Något startar med hastigheten v=0 och accelererar under 2 timmar. När det gått 2 timmar håller det hastigheten 2 km/h. Sedan börjar det bromsa och efter ytterligare två timmar är v=0 och det har stannat.

Hur långt har föremålet kommit?

Nu går det inte att räkna s=vt längre eftersom v inte är konstant.

Däremot kan vi räkna ut arean av en halvcirkel med radien r=2:

$A=\frac{{\mathrm{\pi r}}^2}{2}=\frac{\mathrm{\pi }{2}^2}{2}\approx 6,3$

Föremålet har alltså färdats ungefär 6,3 km på 4 timmar. Är det rimligt? 

Ja, om hastigheten varit konstant v=2 under 4 timmar hade vi kommit 8 km. Nu var den lite lägre i början och slutet, så det känns OK.

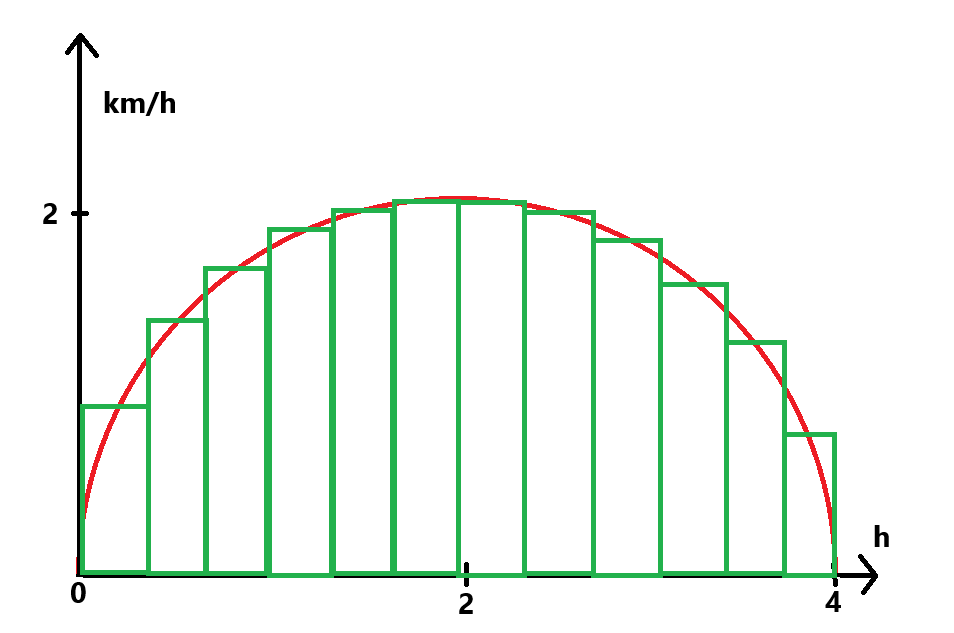
Det man egentligen gör är att man delar upp kurvan i massa små rektanglar, som alla är lätta att räkna ut arean för. Sedan lägger man ihop dem. Läser du Fysik1 nu är det överkurs, men det kommer garanterat i Matte3 eller så.

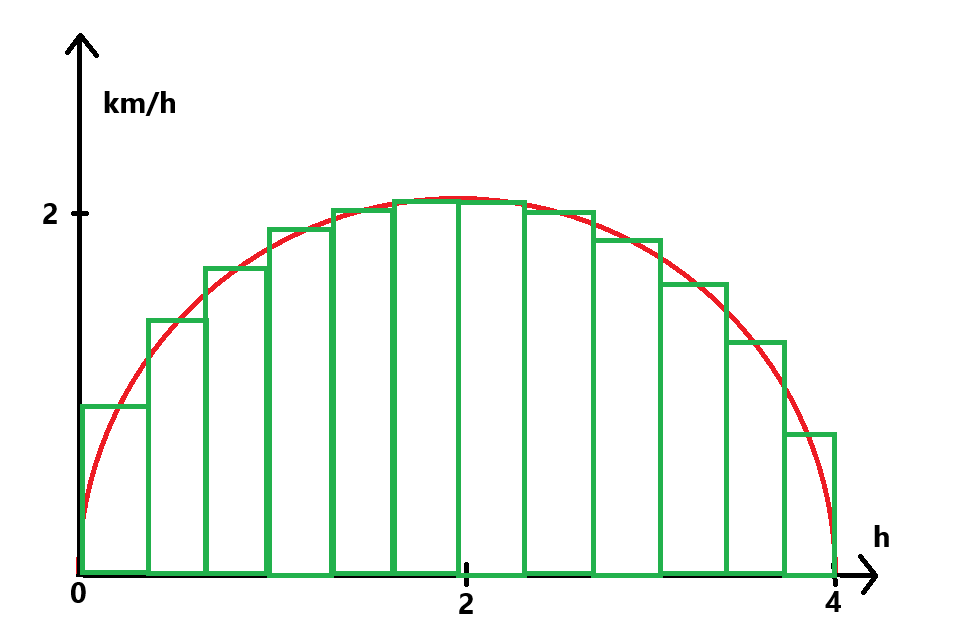
Vet inte om detta var någon sorts svar på din fråga. Återkom gärna.

sictransit skrev:

Jag är inte helt säker på att jag förstår din fråga. Den är inte superlätt att läsa, men jag gör ett försök.

I bilden visas ett v-t-diagram. Man håller konstant hastighet under en timme.

Du vet säkert att s = vt, så om man kör 70 km per timme och kör i en timme, så är sträckan:
s = 70 km/h * 1 h = 70 km

Det är också arean av den streckade rektangeln i bilden. Rektangelns area är ju basen (=1) * höjden (=70).

Om y-axeln är i enheten km/h och x-axeln i enheten h, så blir ju km/h * h = enheten km.

---

Det där med att beräkna arean har med primitiva funktioner och integraler att göra, men det är nog kanske en bit fram i gymnasiekursen. 

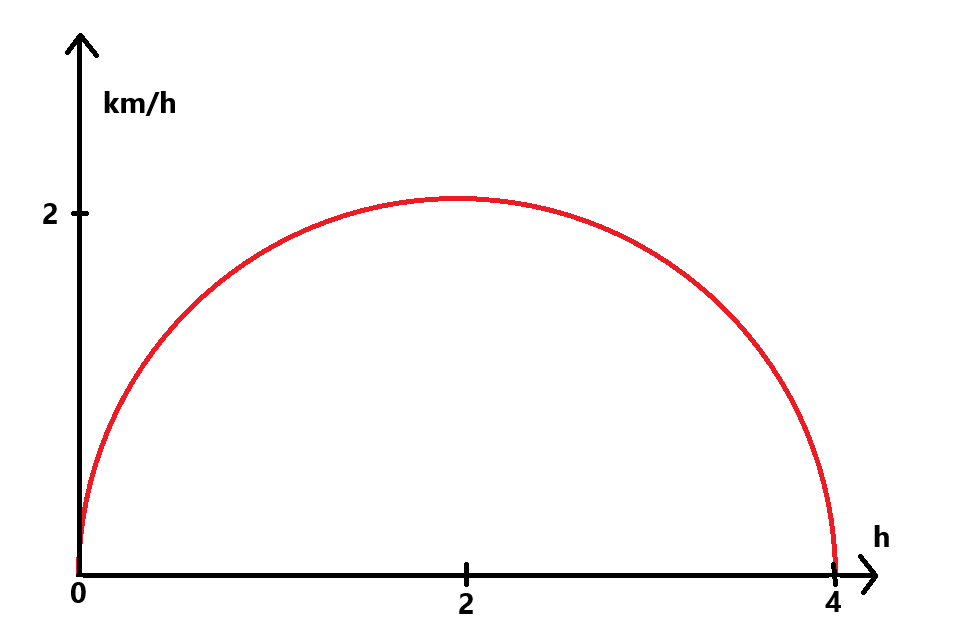
Tänk dig detta v-t-diagram istället:

Något startar med hastigheten v=0 och accelererar under 2 timmar. När det gått 2 timmar håller det hastigheten 2 km/h. Sedan börjar det bromsa och efter ytterligare två timmar är v=0 och det har stannat.

Hur långt har föremålet kommit?

Nu går det inte att räkna s=vt längre eftersom v inte är konstant.

Däremot kan vi räkna ut arean av en halvcirkel med radien r=2:

$A=\frac{{\mathrm{\pi r}}^2}{2}=\frac{\mathrm{\pi }{2}^2}{2}\approx 6,3$

Föremålet har alltså färdats ungefär 6,3 km på 4 timmar. Är det rimligt? 

Ja, om hastigheten varit konstant v=2 under 4 timmar hade vi kommit 8 km. Nu var den lite lägre i början och slutet, så det känns OK.

 

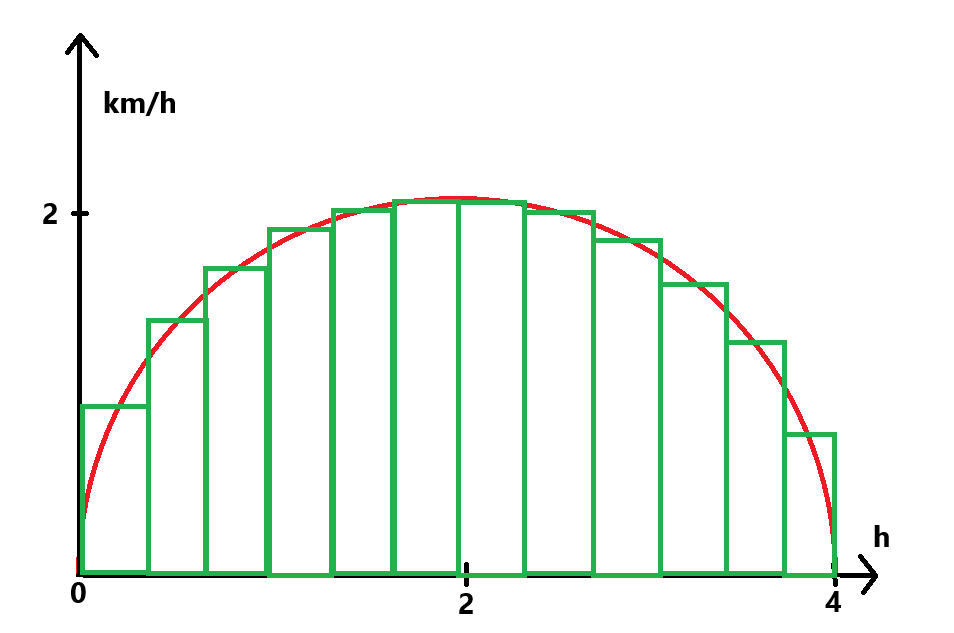
Det man egentligen gör är att man delar upp kurvan i massa små rektanglar, som alla är lätta att räkna ut arean för. Sedan lägger man ihop dem. Läser du Fysik1 nu är det överkurs, men det kommer garanterat i Matte3 eller så.

---

Vet inte om detta var någon sorts svar på din fråga. Återkom gärna.

tack snälla det var tydligt förklaring

Katnisshope skrev:

sictransit skrev:

Jag är inte helt säker på att jag förstår din fråga. Den är inte superlätt att läsa, men jag gör ett försök.

I bilden visas ett v-t-diagram. Man håller konstant hastighet under en timme.

Du vet säkert att s = vt, så om man kör 70 km per timme och kör i en timme, så är sträckan:
s = 70 km/h * 1 h = 70 km

Det är också arean av den streckade rektangeln i bilden. Rektangelns area är ju basen (=1) * höjden (=70).

Om y-axeln är i enheten km/h och x-axeln i enheten h, så blir ju km/h * h = enheten km.

---

Det där med att beräkna arean har med primitiva funktioner och integraler att göra, men det är nog kanske en bit fram i gymnasiekursen. 

Tänk dig detta v-t-diagram istället:

Något startar med hastigheten v=0 och accelererar under 2 timmar. När det gått 2 timmar håller det hastigheten 2 km/h. Sedan börjar det bromsa och efter ytterligare två timmar är v=0 och det har stannat.

Hur långt har föremålet kommit?

Nu går det inte att räkna s=vt längre eftersom v inte är konstant.

Däremot kan vi räkna ut arean av en halvcirkel med radien r=2:

$A=\frac{{\mathrm{\pi r}}^2}{2}=\frac{\mathrm{\pi }{2}^2}{2}\approx 6,3$

Föremålet har alltså färdats ungefär 6,3 km på 4 timmar. Är det rimligt? 

Ja, om hastigheten varit konstant v=2 under 4 timmar hade vi kommit 8 km. Nu var den lite lägre i början och slutet, så det känns OK.

 

Det man egentligen gör är att man delar upp kurvan i massa små rektanglar, som alla är lätta att räkna ut arean för. Sedan lägger man ihop dem. Läser du Fysik1 nu är det överkurs, men det kommer garanterat i Matte3 eller så.

---

Vet inte om detta var någon sorts svar på din fråga. Återkom gärna.

tack snälla det var tydligt förklaring

jag har en annan fråga hur kan förflyttningen här mellan 0 min & 30 min bli 0 km/h?

Hastighet är ju en vektor så den har både storlek och riktning. Diagrammet säger att man börjar fara i 50 km/h. Efter en kvart står man still  och därefter får åker man åt andra hållet. 

Vill du räkna areor så har du en +area ovanför x-axeln och en lika stor -area under. Summan av dem blir noll. 

sictransit skrev:

Hastighet är ju en vektor så den har både storlek och riktning. Diagrammet säger att man börjar fara i 50 km/h. Efter en kvart står man still  och därefter får åker man åt andra hållet. 

Vill du räkna areor så har du en +area ovanför x-axeln och en lika stor -area under. Summan av dem blir noll. 

ja nu förstår jag  tack så mycket!!