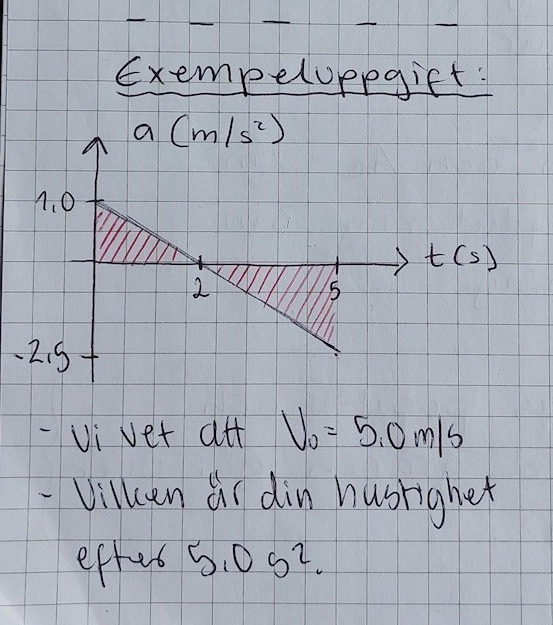
Hastigheten efter 5.0 s

Hej.

Du kan anvönda sambandet att accelerationen a(t) är tidsderivatan av hastigheten v(t), dvs a(t) = v'(t).

Det betyder att hastigheten v(t) är en primitiv funktion till accelerationen a(t).

Kommer du vidare då?

Inte riktigt... jag är med på att arean under a-t grafen visar hastighetsförändringen. Jag vet däremot inte hur jag kör vidare med det. 

Nästan. Grafens höjd visar hastighetsförändringen (dvs accelerationen).

=====

Där accelerationsgrafen ligger ovanför t-axeln så är accelerationen positiv och hastigheten ökar.

-> Arean av området mellan grafen och t-axeln visar då hur mycket hastigheten ökar.

=====

Där accelerationsgrafen ligger under t-axeln så är accelerationen negativ och hastigheten minskar.

-> Arean av området mellan grafen och t-axeln visar hur mycket hastigheten minskar.

Kommer du vidare då?

Jag hänger med på det du säger men vet fortfarande inte hur jag ska ta mig an uppgiften. 

Grafen skapar två trianglar precis som du ritat ut. Arean mellan grafen och x-axeln visar hastighetens ökning eller minskning. Då kan du beräkna vardera triangels area och addera dem. (Obs att arean under grafen blir negativ). Kommer du fram till ett svar då?

Dr.scofield skrev:

Jag hänger med på det du säger men vet fortfarande inte hur jag ska ta mig an uppgiften. 

Hastighetsändringen blir $\Delta v=\int_{0}^{5}a(t)\operatorname dt$

Det är viktigt att du förstår varför.