Hej! Kan någon hjälpa mig med ekvationen

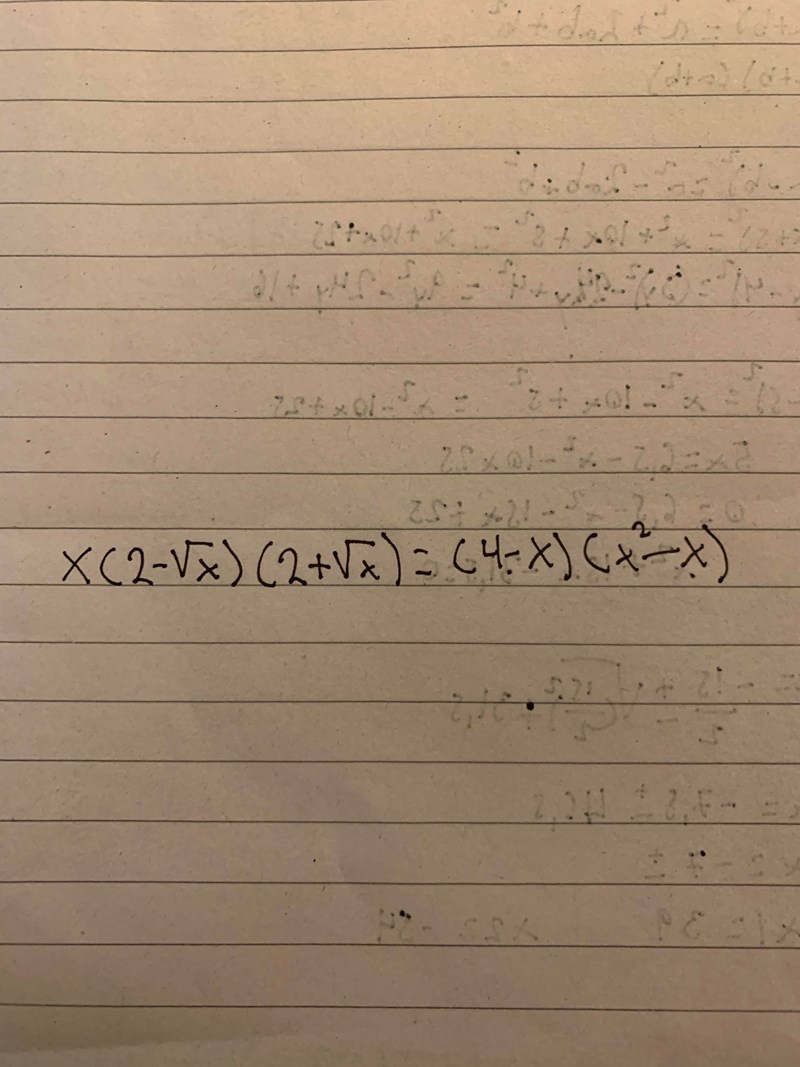
Ser du faktorn (4-x) på båda HL och VL?

Hej och välkommen till Pluggakuten!

Börja med att multiplicera ihop parenteserna i vänsterledet. Du kan använda konjugatregeln till det om du vill.

Samla sedan alla termer på ena sidan av likhetstecknet, faktorisera och använd nollproduktmetoden.

Kan du visa hur man använder konjujatregeln när roten ur är med?Tack!

Vsd får du när du kvadrerar en rot? 

Hokuspokus skrev:

Kan du visa hur man använder konjujatregeln när roten ur är med?Tack!

Du använder den på precis samma sätt som vanligt. Visa hur du försöker, så skall vi hjälpa dig om du kör fast.

Problemet är att jag redan kört fast :) kommer inte längre 

Hittar inga liknande exempel

Hokuspokus, det räcker med en tråd om varje fråga. jag tog bort din dubbelpost. /moderator

Konjugatregeln lyder $(a-b)(a+b)=a^2-b^2$.

I ditt fall är $a=2$ och $b=\sqrt{x}$, vilket betyder att $(2-\sqrt{x})(2+\sqrt{x})=2^2-(\sqrt{x})^2$.

Kan du fortsätta själv?

Stämmer det här?

2^2-($\sqrt{x}$)^2= 4x^2+x^2

3x^2-2^2-$\sqrt{x}$^2

3*x*x-2*2-$\sqrt{}$*x*x

3x^-4-$\sqrt{x}$

x(3x-4)=0

x=0

Hokuspokus skrev:

Stämmer det här?

Det verkar som om du inte har skrivit upp ursprungsekvationen. Det gör det svårt att följa med i resonemanget. 

$x(2-\sqrt{x})(2+\sqrt{x})=(4-x)(x^2-x)$

2^2-($\sqrt{x}$)^2= 4x^2+x^2

Du har tappat bort ett x i VL och det mesta av HL. Du borde ha brutit ut ett x i andra faktorn i HL. Det borde ha blivit

$x(2^2-(\sqrt{x})^2)=(4-x)x(x-1)$ förenkla vänsterledet

$x(4-x)=(4-x)x(x-1)$   förkorta bort x och (4-x)

$1=x-1$

Kommer du vidare?

Glöm inte att kontrollera lösningen när du har fått fram ett värde på x.