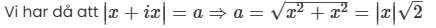Hitta alla möjliga värden på a

1. Antagligen genom att genomföra lösningen för negativa x.

2a,  Ja, du borde ha skrivit ut att periodiciteten för sin och cos ger flera lösningar.

2b. Hade du gjort det hade du inte behövt fråga   :-)

Men gör jag samma sak för negativa x får jag ju ändå -x / -x = 1.

tan(x) = 1 har lösningen $x =3\pi/4$ också.

Nu är jag väldigt förrvirrad men enligt formelbladet:

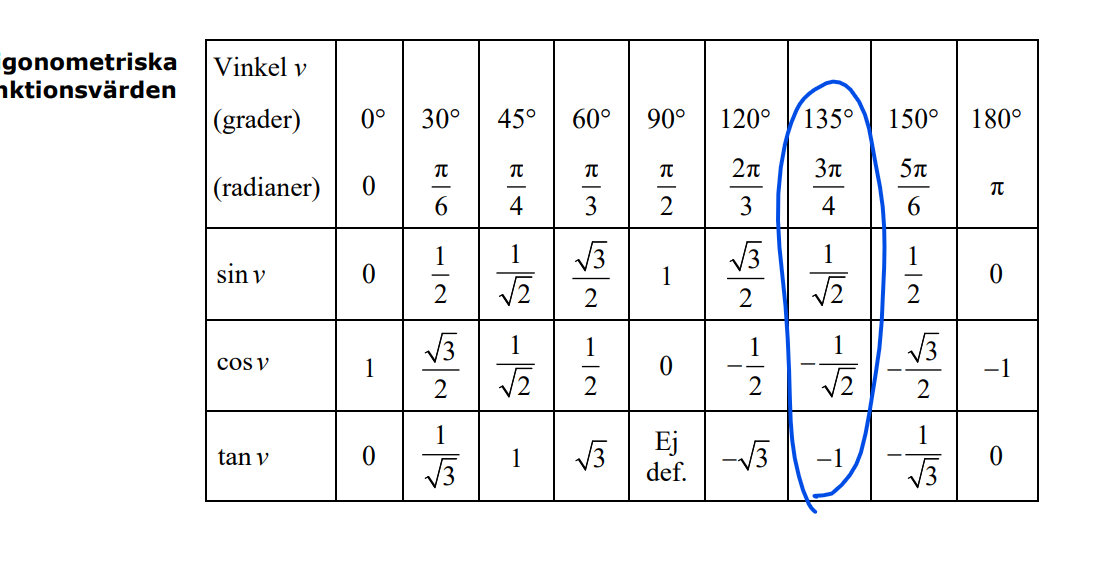
Hm, förlåt, jag tänkte inte efter.

Absolutbeloppet av talen är $a$. 
Vi har då att $|x+ix| = a \Rightarrow a = \sqrt{x^2+x^2} = |x|\sqrt 2$

Ekvationen blir då
$\displaystyle a\left(\cos x + i\sin x\right) = \left|x\right|\sqrt 2\left(\cos \frac \pi 4 + i \sin \frac \pi 4\right)$

Dela upp det i två olika fall: $x$ är positivt, $x$ är negativt.

Men jag förstår inte, måste man alltid sätta x inom absolutbeloppstecken sådär? Jag har löst andra uppgifter tidigare med komplexa tal och inte behövt göra så. Dvs. som du gjorde enligt nedan: 

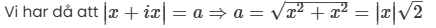
Och hur blir argumentet sedan 3*pi/4?

Anonym_15 skrev:

Men jag förstår inte, måste man alltid sätta x inom absolutbeloppstecken sådär? Jag har löst andra uppgifter tidigare med komplexa tal och inte behövt göra så. Dvs. som du gjorde enligt nedan: 

Tänk dig om $x=-1$. Om vi använder att $|x+ix| = \sqrt{2} x$ får vi att $|-1-i| = -\sqrt 2$, vilket inte är korrekt, ett absolutbelopp är alltid positivt. Däremot gjorde jag ett mistag, tänkte lite för snabbt och ekvationen jag skrev efter är inte korrekt.   

Mer detaljerad uträkning på absolutbeloppet:

$|x+ix| = \sqrt{x^2 + x^2} = \sqrt{2x^2} = \sqrt 2 \cdot \sqrt{x^2}$

$x$ är ju reellt. Oberoende värde på $x$ blir $\sqrt{x^2}$ ett positivt tal. Därför kan vi inte säga att de tar ut varandra. $\sqrt{x^2} = x$ gäller bara om $x \geq 0$. Om $x$ är negativt kommer $\sqrt{x^2}$ fortfarande vara positivt, alltså inte lika med $x$.

Därför måste vi sätta ett absolutbelopp på det. Vi behöver göra det i detta fall eftersom vi inte vet om $x$ är positivt eller negativt. Det kan vara antingen eller!

Anonym_15 skrev:

Och hur blir argumentet sedan 3*pi/4?

Jag skrev ett svar men jag kom på ett mycket snabbare sätt. Jag lämnar kvar mitt gamla svar men jag tycker inte det är bra. Läs det nya!

Lösningsförslag: 

AlexMu skrev:

Anonym_15 skrev:

Och hur blir argumentet sedan 3*pi/4?

Jag skrev ett svar men jag kom på ett mycket snabbare sätt. Jag lämnar kvar mitt gamla svar men jag tycker inte det är bra. Läs det nya!

 

Jag skrev detta tidigare, lite sämre lösning än nr  2

Vi vet att $a = |x+ix|$ enligt uppgiftsformuleringen.

Då är $a = |x|\sqrt{2}$ 

Substituering i uttrycket ger oss:

$|x|\sqrt 2(\cos x + i\sin x) = x + ix$

Fall 1: $x > 0$ är det fall du redan har löst, därför ignorerar jag det. 
Fall 2. $x < 0$ (jag ignorerar fallet $x=0$, rätt ointressant)

Då är $|x| = -x$, så ekvationen blir 

$-x\sqrt 2(\cos x + i\sin x) = x+ ix$. 

Vi vet att $\displaystyle1+i = \sqrt 2\left(\cos \frac \pi 4 + i\sin \frac \pi 4\right)$

Division med $x$ och substituering av detta värde ger oss: 

$\displaystyle -\sqrt 2\left(\cos x + i\sin x\right) =\sqrt 2\left(\cos \frac \pi 4 + i\sin \frac \pi 4\right)$

Division med $\sqrt 2$:

$\displaystyle -\left(\cos x + i\sin x\right) =\cos \frac \pi 4 + i\sin \frac \pi 4$

Det kan vara trevligt att skriva om detta med eulers formel:

Högerled blir $e^{i\frac\pi 4}$. Vänsterled blir $-1 \cdot e^{ix}$, vidare är $-1 = e^{i\pi}$. 
Så vi kan skriva om vänsterled som $e^{i\pi}\cdot e^{ix} = e^{i(x+\pi)}$

Då är 

$\displaystyle e^{i(x+\pi)} = e^{i\frac\pi 4}$

Nu har vi slutligen något trevligt att jobba med!

Vi har då att $\displaystyle i(x+\pi) = i\frac \pi 4$
Vilket förenklas till $x = -\frac{3\pi}4$
Då $a = |x|\sqrt 2$ får vi det vi önskade. (ignorerat $2\pi n$)

Lösningsförslag: 

Visa spoiler

Från ekvationen $a(\cos x + i\sin x) = x + ix$ kan vi skriva om VL med Eulers formel som $a\cdot e^{ix}$
Högerledet kan först faktoriseras för att sedan också skrivas med Eulers: 

$x+ix = x(1+i) = x\sqrt 2 \cdot e^{i\frac\pi 4}$

Då är $\displaystyle a \cdot e^{ix} = x\sqrt 2 \cdot e^{i\frac\pi 4}$

Multiplikation av båda led med $e^{-ix}$ ger 

$\displaystyle a = x \sqrt 2 \cdot e^{i\left(\frac\pi 4 - x\right)}$

$a$ är ett absolutbelopp och då måste vara reellt. 
$x$ är reellt, $\sqrt 2$ är reellt. Det enda som måste uppfyllas är att $\displaystyle e^{i\left(\frac\pi 4 - x\right)}$ är reellt. Detta sker när imaginärdelen är 0 (eller när $x=0$). 

Med Eulers formel: 

$\displaystyle e^{i\left(\frac\pi 4 - x\right)} = \cos\left(\frac\pi 4 - x\right) + i\sin\left(\frac \pi 4 - x\right)$. 

Det enda kravet är då att $\sin\left(\frac \pi 4 - x\right) = 0$, vilket har lösningarna 
$\displaystyle x = \frac{\pi}4 + 2\pi n$ för något heltal $n$ och 
$\displaystyle x = -\frac{3\pi}4 + 2\pi n$ för något heltal $n$

Sätt in dessa värden för $x$ i uttrycket 

$\displaystyle a = x \sqrt 2 \cdot e^{i\left(\frac\pi 4 - x\right)}$

Så fås det önskade svaret.

Det är en bra lösning som jag själv funderade på men höll tillbaka då tidigare diskussion i andra trådar har varit att favorisera polär form och inte exponentialform. Jag tycker dock detta är bästa sättet men det beror på var i boken uppgiften kommer, vilket var oklart.

med en halverad period kan lösningarna reduceras.