Hitta en isomorfi mellan en av de två möjliga grupperna av ordning 4 och C2xC2

Hej!

Jag sitter med följande uppgift:

"Show that the two distinct groups of order 4 are isomorphic to $C_4$ and $C_2 \times C_2$" (Discrete Mathematics av Biggs uppg 20.6.4)

Boken har inget facit för uppgiften men har en tabell som visar de två distinka grupperna av ordning 4. Här är en av de:

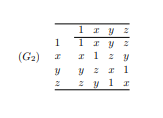
Jag får grupptabellen för den direkta produkten mellan

$C_2 = <x> = \left\{1,x\right\}$

$C_2=<y>=\left\{1,y\right\}$

till (här har jag tagit hjälp av AI för att mina plottriga anteckningar inte är så läsbara, men jag har dubbelkollat att det är samma som jag skrivit ner).

Jag kanske har tänkt fel för grupptabellen för den direkta produkten. För när jag ska hitta en isomorfi mellan de två grupptabellerna så ser jag att i den andra grupptabellen (för $C_2 \times C_2$) så har alla element ordning 2. Det gäller inte för den första grupptabellen. Måste inte ordningen vara samma för alla gruppelement för att en isomorfi ska finnas?