Hitta ett komplext tal från talplanet
Hej,
Skulle någon kunna förklara vilka steg jag har tagit fel här, svaret 3*60grader känns fel.
När dem säger talet, vad är det för tal dem är ute efter? Vill dem ha punkterna i systemet eller vinkeln?
Tack på förhand
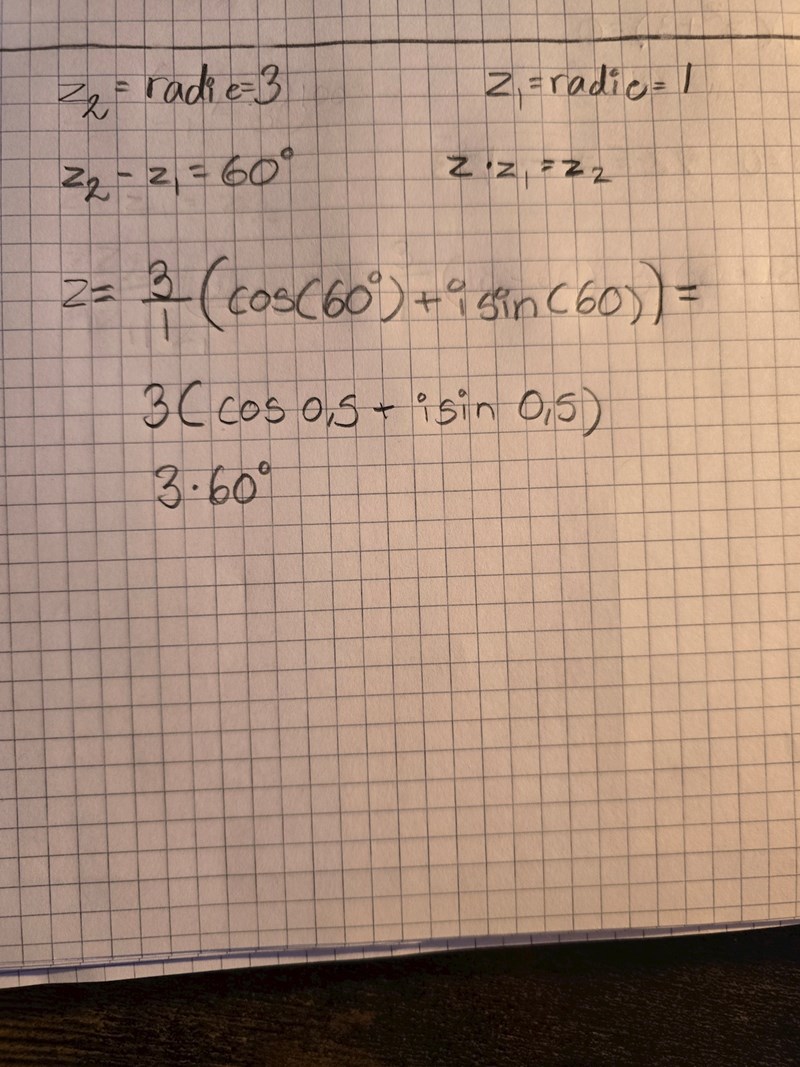
De söker ett komplext tal i valfri form. Detta ska innefatta som vanligt ett belopp och och ett argument.
Mrpotatohead skrev:De söker ett komplext tal i valfri form. Detta ska innefatta som vanligt ett belopp och och ett argument.
Tack för ditt svar!
Då tänker jag att 3an är beloppet och 60 grader som argumentet, men det känns väldigt fel då avståndet mellan z1 och z3 är 60 grader
Du bör skriva Arg z när du avser argumentet, dvs vinkeln, för z.
Du bör skriva Abs z när du avser absolutbeloppet av z, dvs avståndet mellan z och origo.
Då gäller följande:
Arg z2 - Arg z1 = 60°
Abs z1 = 1
Abs z2 = 3
Vi har att z*z1 = z2, vilket ger z = z2/z1.
Enligt räknereglerna för komplexa tal på polär form så gäller det att
Arg z = Arg z2 - Arg z1 = 60°
Abs z = Abs z2/Abs z1 = 3/1 = 3
Vi får alltså z = 3(cos(60°)+i*sin(60°)) = 3*0,5 + i*
Yngve skrev:Du bör skriva Arg z när du avser argumentet, dvs vinkeln, för z.
Du bör skriva Abs z när du avser absolutbeloppet av z, dvs avståndet mellan z och origo.
Då gäller följande:
Arg z2 - Arg z1 = 60°
Abs z1 = 1
Abs z2 = 3
Vi har att z*z1 = z2, vilket ger z = z2/z1.
Enligt räknereglerna för komplexa tal på polär form så gäller det att
Arg z = Arg z2 - Arg z1 = 60°
Abs z = Abs z2/Abs z1 = 3/1 = 3
Vi får alltså z = 3(cos(60°)+i*sin(60°)) = 3*0,5 + i*
Tusen tackar för ditt utförliga svar nu förstår jag äntligen! :)




