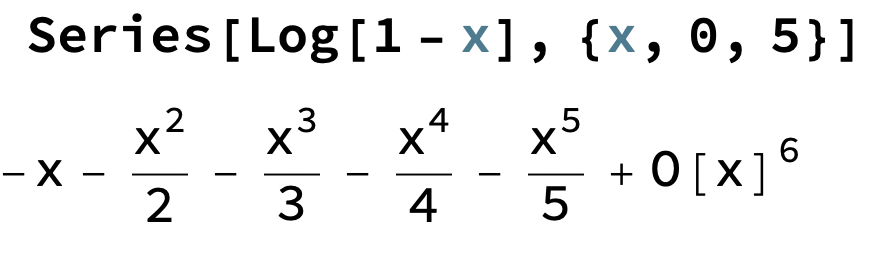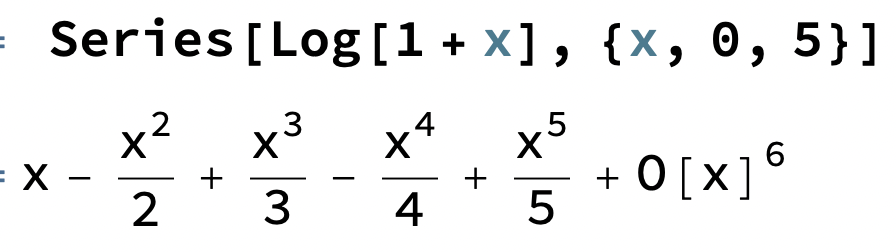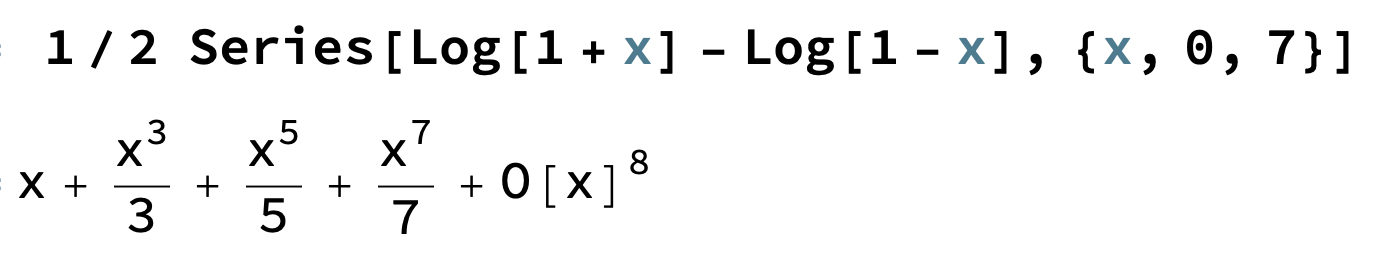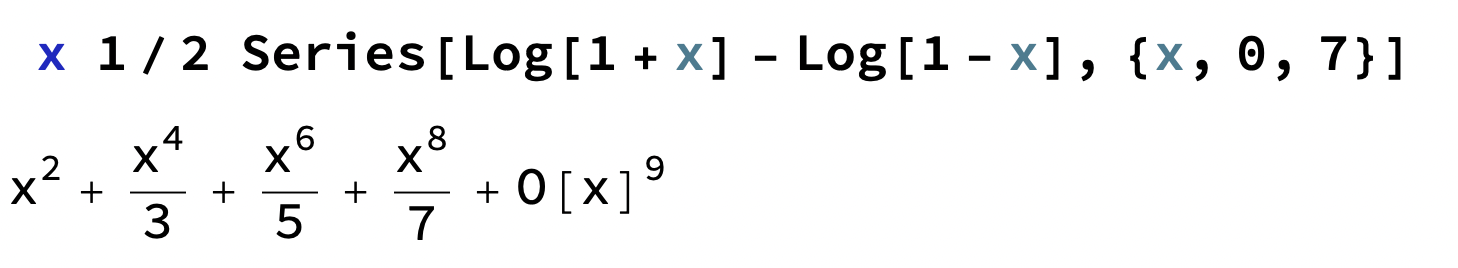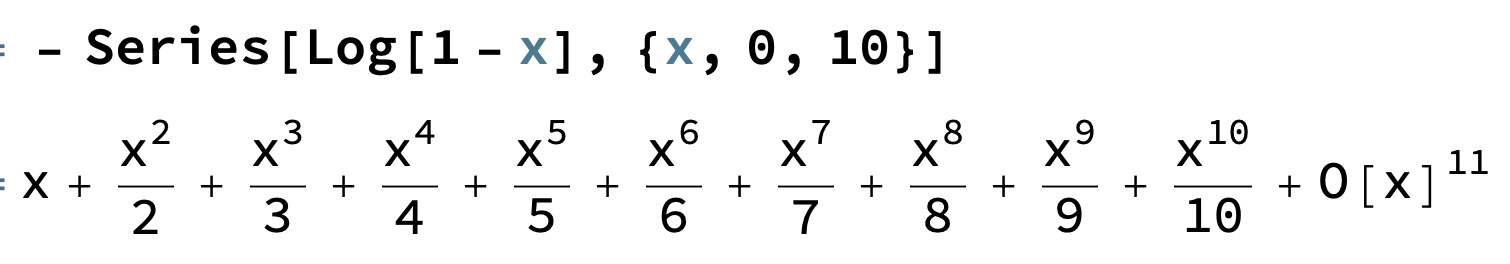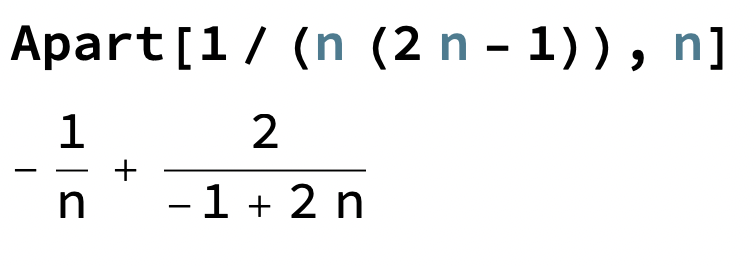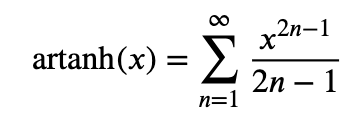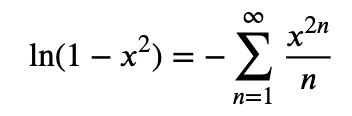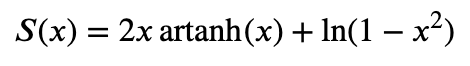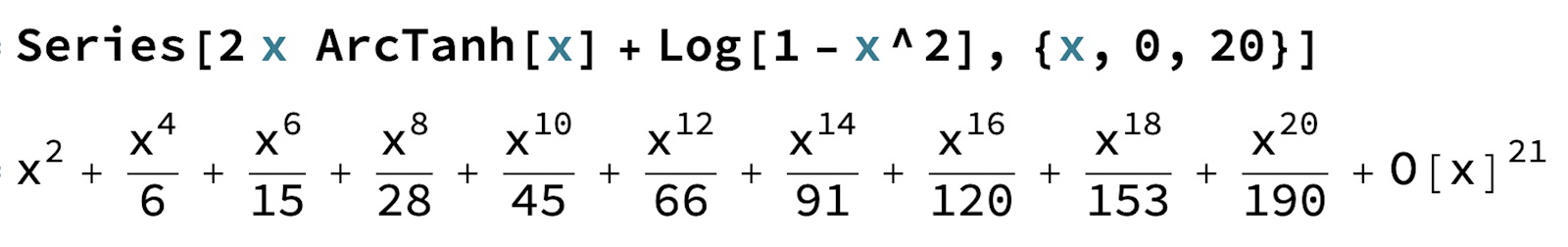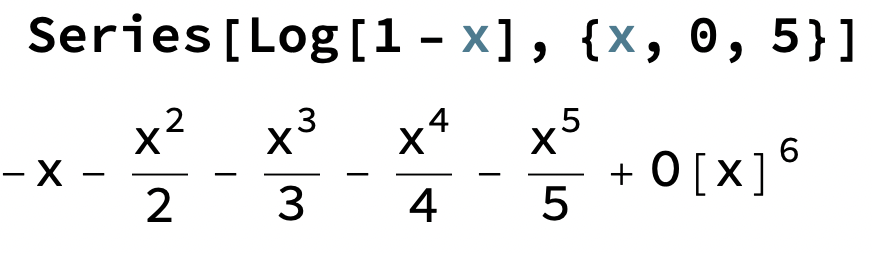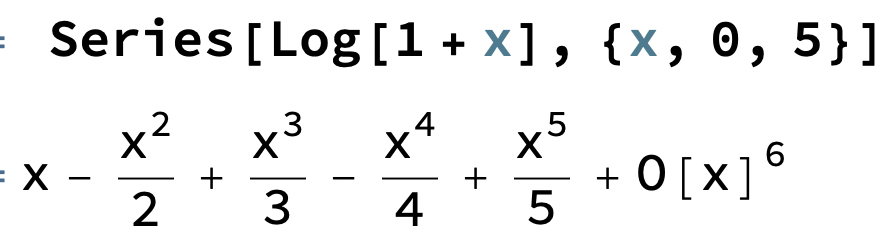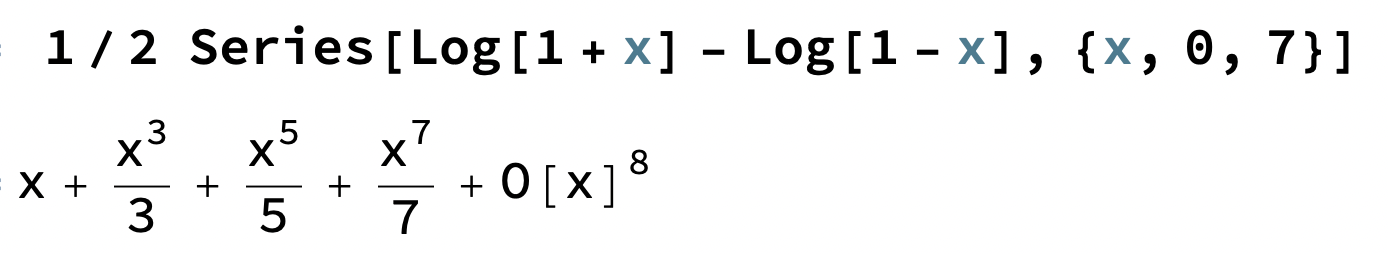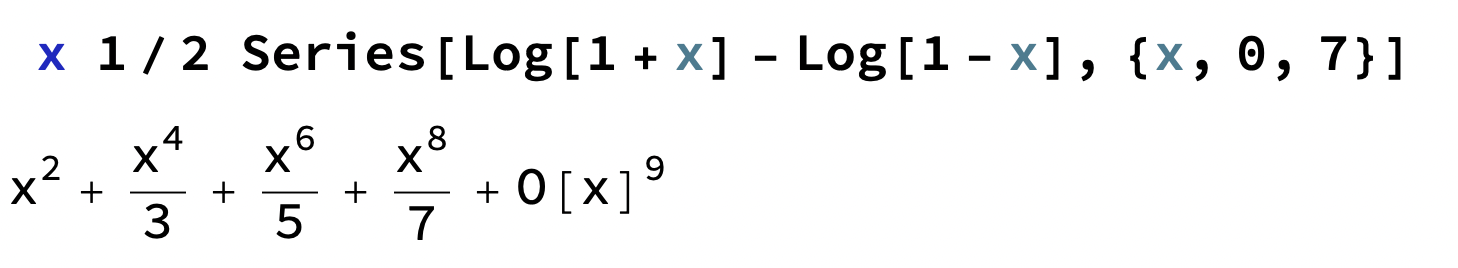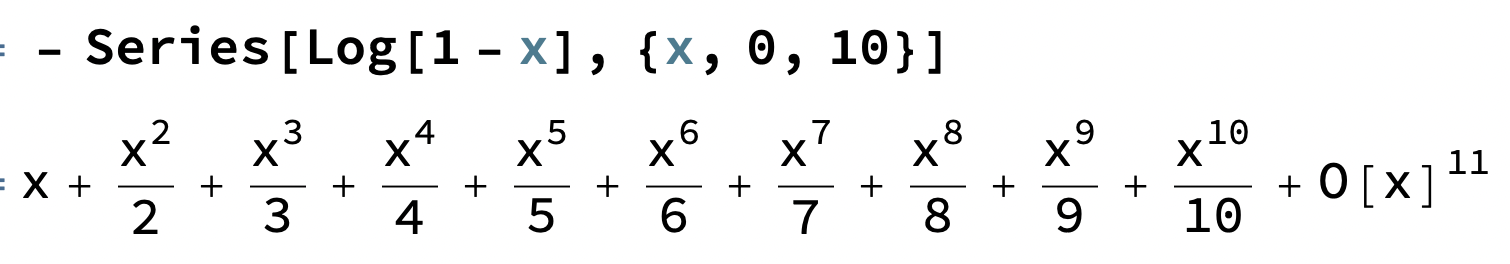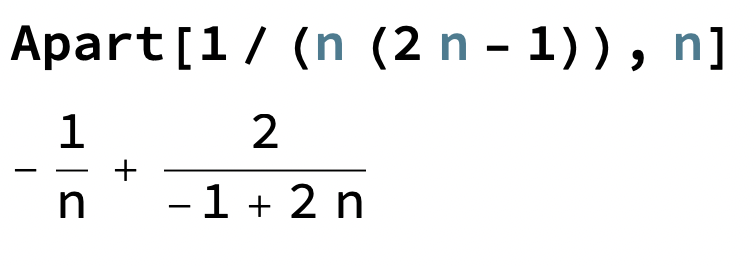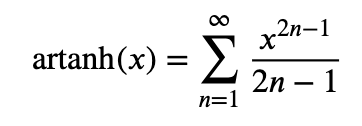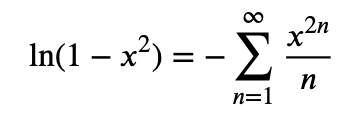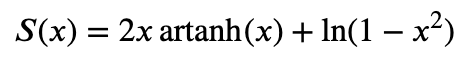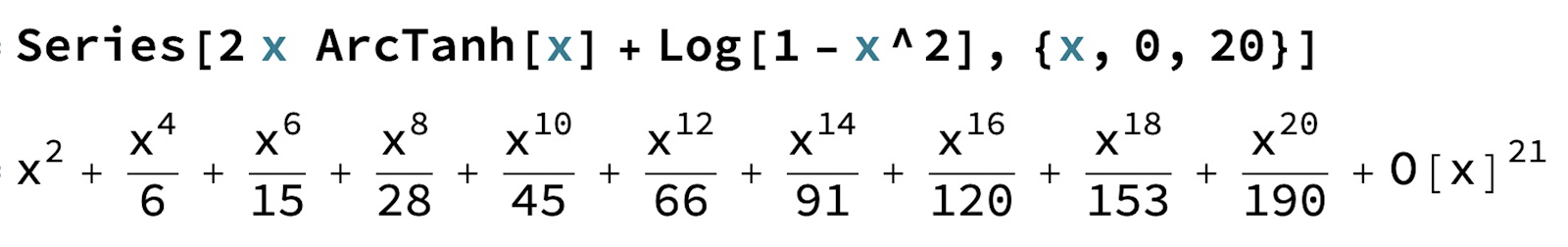Hitta funktionen för taylorsserie
Behöver hjälp med hur jag ska tänka kring sånna här problem 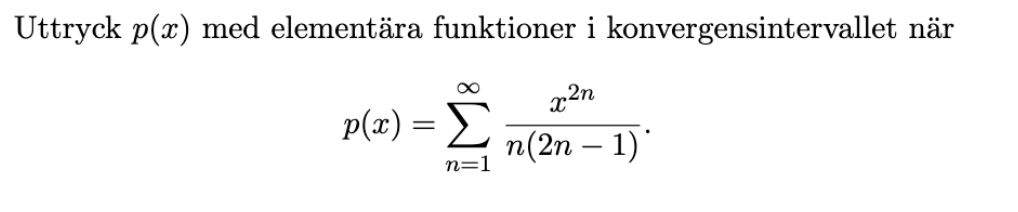
Tricket här är att studera olika fall av ln(1±x)
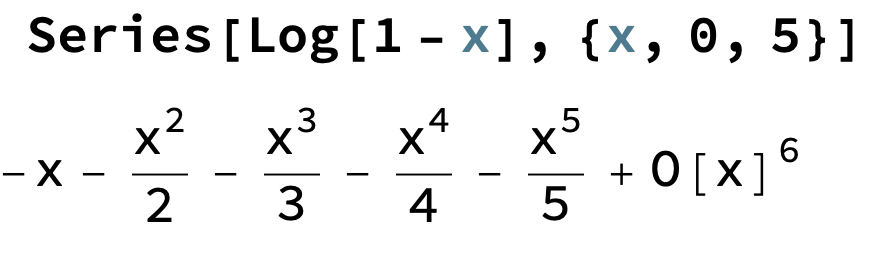
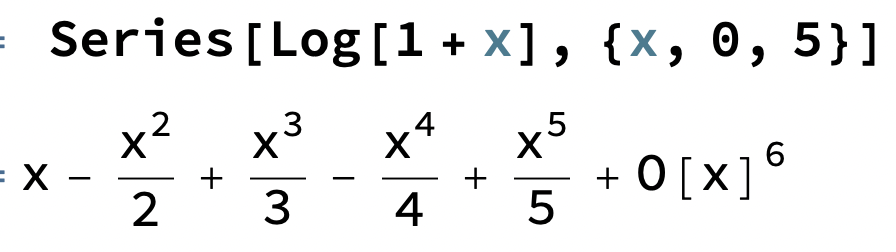
Här kan man "förstärka" eller "förminska" (eliminera) de jämna eller udda termnerna genom att addera eller subtrahera dessa serier
Om vi tar 1/2 ( ln(1+x) - ln(1-x) ) fås
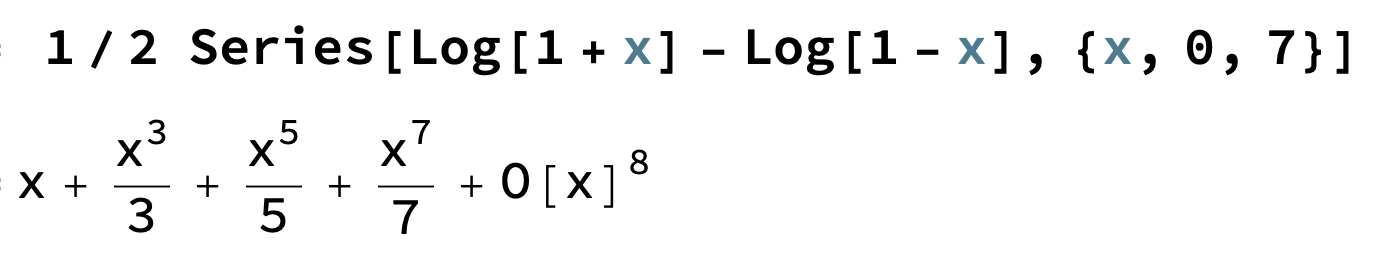
som ger oss udda potenser med udda nämnare men
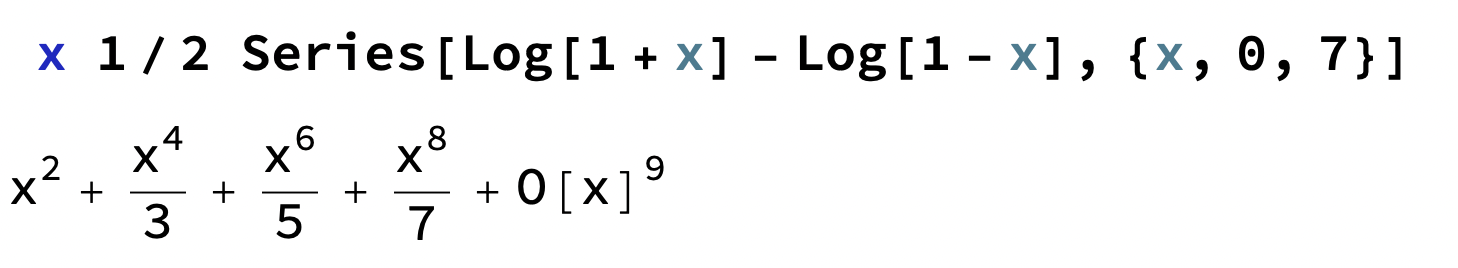
ger jämna potenser med udda nämnare.
Samt
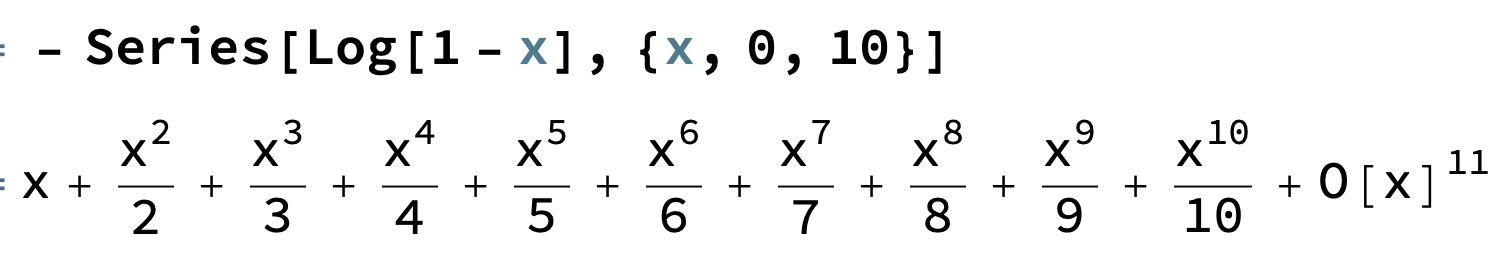
Om vi sedan part.bråkuppdelar (givet vi får det i oändligheten vid separation av summering, men så länge vi är inom konvergensradien är det säkert OK) får vi
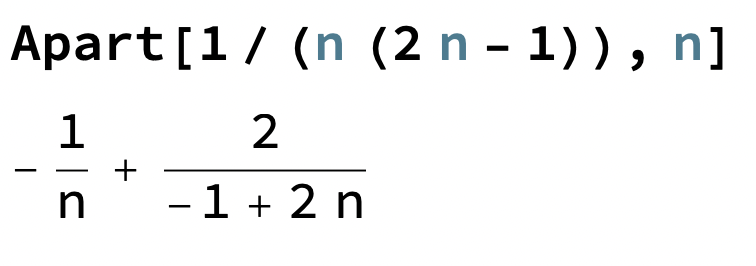
och nu kan vi kombinera delarna.
Man bör komma fram till något i stil med

Om man har bra minne kanske man kommer ihåg att
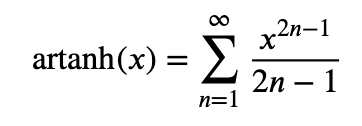
och
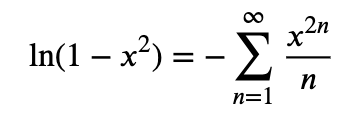
vilket ger att
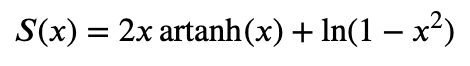
Men det är inte alltid man kommer ihåg allt.
Trinity2 skrev:Tricket här är att studera olika fall av ln(1±x)
Här kan man "förstärka" eller "förminska" (eliminera) de jämna eller udda termnerna genom att addera eller subtrahera dessa serier
Om vi tar 1/2 ( ln(1+x) - ln(1-x) ) fås
som ger oss udda potenser med udda nämnare men
ger jämna potenser med udda nämnare.
Samt
Om vi sedan part.bråkuppdelar (givet vi får det i oändligheten vid separation av summering, men så länge vi är inom konvergensradien är det säkert OK) får vi
och nu kan vi kombinera delarna.
Man bör komma fram till något i stil med
Om man har bra minne kanske man kommer ihåg att
och
vilket ger att
Men det är inte alltid man kommer ihåg allt.
Hur vet man vilken serie man ska studera?
Koizenu skrev:Trinity2 skrev:Tricket här är att studera olika fall av ln(1±x)
Här kan man "förstärka" eller "förminska" (eliminera) de jämna eller udda termnerna genom att addera eller subtrahera dessa serier
Om vi tar 1/2 ( ln(1+x) - ln(1-x) ) fås
som ger oss udda potenser med udda nämnare men
ger jämna potenser med udda nämnare.
Samt
Om vi sedan part.bråkuppdelar (givet vi får det i oändligheten vid separation av summering, men så länge vi är inom konvergensradien är det säkert OK) får vi
och nu kan vi kombinera delarna.
Man bör komma fram till något i stil med
Om man har bra minne kanske man kommer ihåg att
och
vilket ger att
Men det är inte alltid man kommer ihåg allt.
Hur vet man vilken serie man ska studera?
Erfarenhet, men arctanh hör till de mera "udda" i svensk matematikundervisning.
Kan man
e^x
ln (1+x)
(1+x)^a
sin(x)
cos(x)
arctan(x)
(Månsson, sid. 272)
kommer man långt. Sedan är det lite pussel att få ihop dem genom att manipulera dem genom att multiplicera/dividera med x, någon linjärkombination, byta x mot x^2 etc.