Hitta gränser i området
jag ritar den såhär
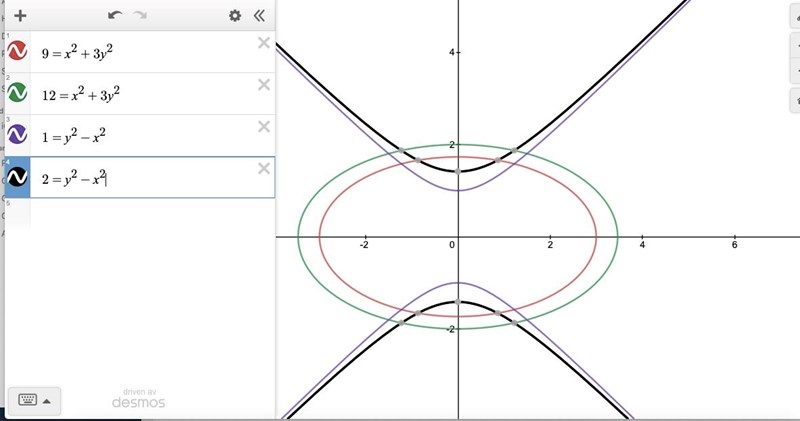
och jag antar att vi är ute efter detta området som jag markerar med orange i bilden nedan:
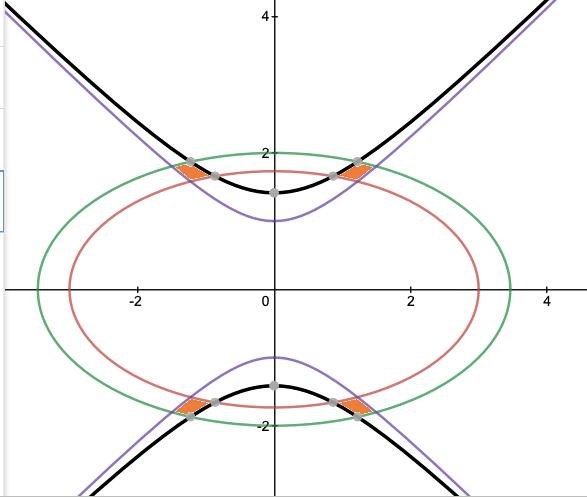
Men undrar hur man ska veta vad det är för gränser av döma av bilden,,
Vad jag kan se har du skissat korrekt.
Gränserna hittar du genom att först sätta ekv1 och ekv3 i ett ekv. system av andra graden. Därefter ekv1 och ekv4, ekv.2 och 3 och slutligen ekv.2 och 4. Eftersom alla potenser =2, blir systemen inte särskilt svåra att lösa, men däremot tämligen tidskrävande. Latmasken gör nedanstående något vågade fundering. Vore väldigt roligt om du kunde kontrollera med den metod som jag tror du redan har valt. Blir det övermäktigt och du har tillgång till facit är en dålig människa lätt förledd.
Låt integranden vara f(x,y). På grund av symmetrin är de fyra orangea delområdena du ritat kongruenta. Symmetrin medför också att absolutvärdet av f blir lika i motsvarande punkter i alla de fyra områdena. f växlar heller inte tecken inom något av områdena. Således blir integralen lika i de fyra områdena sånär som på tecken. Eftersom x2+3y2 >=9 är nämnaren i f alltid positiv. Integrandens tecken bestäms således helt av täljaren xy, som är positiv i första och fjärde kvadranten och negativ i andra och tredje. Integralen av f i de fyra områdena annullerar således varandra, varför integralen över hela D blir 0.
Mvh
Om du inför elliptiskt polära koordinater blir dubbelintegralen förhoppningsvis enklare att beräkna.
och
ger
där
och
som ger gränserna.
.
Integranden blir
och differentialytelementet
,
så integralen som ska beräknas kan skrivas som två itererade enkelintegraler.
Den inre integralen beräknas till
som slutligen ger dubbelintegralen

