Hitta gränsvärdet

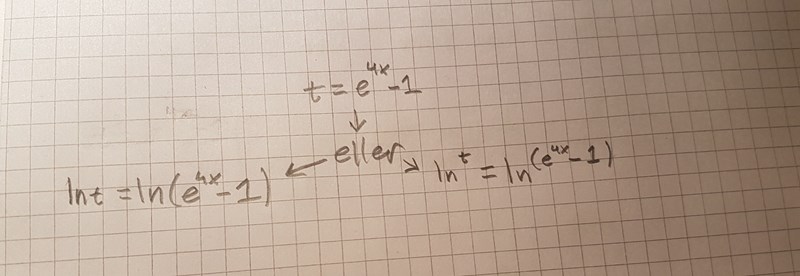
Jag skulle substituera $e^x=t$ och sedan förkorta bråket man får.

Påminner om tekniken i din förra gränsvärdesfråga

Trixa lite så du kan nyttja standardgränsvärdet

$\lim_{x\to 0}\dfrac{e^x-1}{x}=1$.

dr_lund skrev:

Påminner om tekniken i din förra gränsvärdesfråga

Trixa lite så du kan nyttja standardgränsvärdet

$\lim_{x\to 0}\dfrac{e^x-1}{x}=1$.

Det är dit jag försökte komma genom att sätta t=((e^4x)-1) , men anar att du menar att jag ska hitta en annan väg. Lyckas inte komma på hur jag ska göra. 

SvanteR skrev:

Jag skulle substituera $e^x=t$ och sedan förkorta bråket man får.

Får inte till det ändå , vad gör jag för fel? 

1 kommer inte längre, 

2 får  0 som lösning

3 nämnaren blir 0

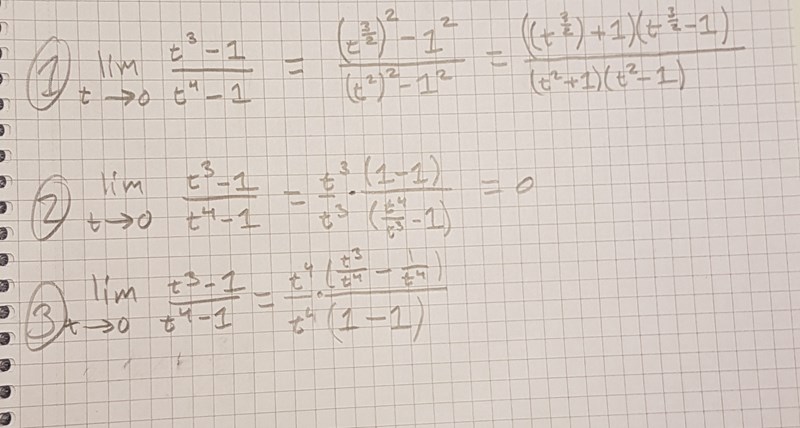
Du kan skriva det som:

$\lim_{x\to 0}\frac{e^{3x}-1}{x}\cdot \frac{x}{e^{4x}-1}=$

$f'(0)\cdot \frac{1}{g'(0)}$

med lämpligt valda funktioner $f(x)$ samt $g(x)$.

Gör inget variabelbyte. Tomas80:s tips är bra.

Notera att vi inte får förändra ursprungligt bråk, men väl förlänga med faktor 1, bokförd på ett slugt sätt.
Jag börjar så avslutar du:

$\dfrac{e^{3x}-1}{3x}\cdot\dfrac{3x}{e^{4x}-1}$

poijjan skrev:

SvanteR skrev:

Jag skulle substituera $e^x=t$ och sedan förkorta bråket man får.

Får inte till det ändå , vad gör jag för fel? 

1 kommer inte längre, 

2 får  0 som lösning

3 nämnaren blir 0

 

Du har ju fått tips om andra metoder också, men om du vill fortsätta på min metod måste du faktorisera $t^3-1$. Det gör man på följande sätt:

Gissa en rot till $t^3-1=0$

Använd roten för att identifiera en faktor och gör polynomdividion för att få den andra faktorn.

Sedan kan du också faktorisera nämnaren ett steg till med konjugatregeln.

dr_lund skrev:

Gör inget variabelbyte. Tomas80:s tips är bra.

Notera att vi inte får förändra ursprungligt bråk, men väl förlänga med faktor 1, bokförd på ett slugt sätt.
Jag börjar så avslutar du:

$\dfrac{e^{3x}-1}{3x}\cdot\dfrac{3x}{e^{4x}-1}$

Tipset att förlänga som du visade var ju snyggt, hänger dock inte med på omskrivningen $f\text{'}\left(0\right)·\frac{1}{g\text{'}\left(0\right)}$, vi har inte börjat med derivator ännu, och minnet från gymnasiet sviktar.. kan nog hänga med på den om någon vecka då jag är lite mer uppdaterad.

Aja , har testat lite olika vägar utan att komma i mål, anar att jag vill få upp nämnaren i täljaren på något vänster ??

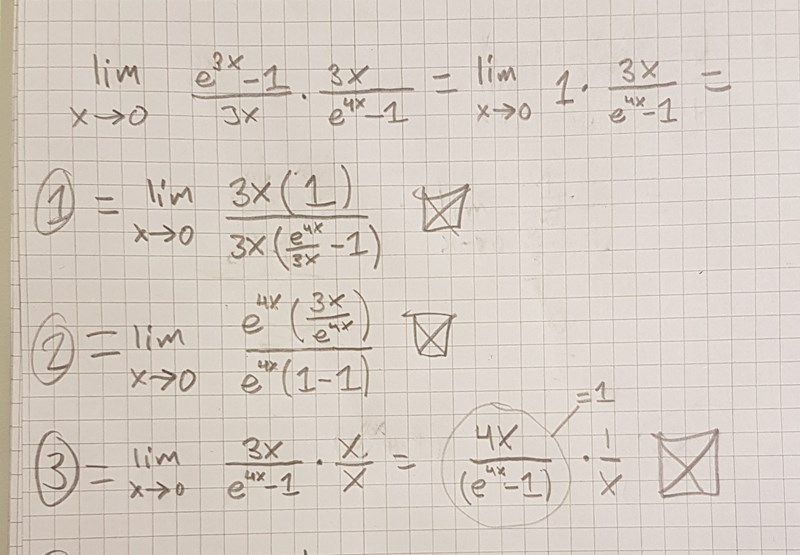
Nja. Fortsätt på mitt spår, men nu med

$e^{4x}-1$. Gör inget att den står i nämnaren just be careful. Inget tjafs med derivator, detta löser vi elegant med min tankegång., 

$3x\cdot x=3x^2$, inte 4x.

dr_lund skrev:

Nja. Fortsätt på mitt spår, men nu med

$e^{4x}-1$. Gör inget att den står i nämnaren just be careful. Inget tjafs med derivator, detta löser vi elegant med min tankegång., 

Tack för ditt tålamod :) Måste vara ganska nära nu , har fått fram rätt svar i en faktor (3/4) så jag anar att det är OK att stryka x/x innan jag tänker vad som händer om jag petar in 0 ? Finns det någon bra och hyffsat enkel förklaring till detta, eller gör man bäst i att bara acceptera ?

Förutsatt att jag gjort rätt i övrigt då 

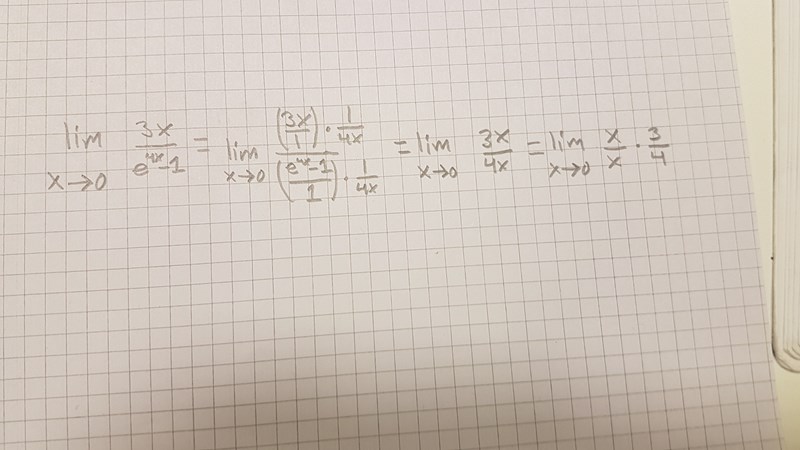
Ser bra ut. Det blir ett ändligt gränsvärde.

Anm Du kan frimodigt förkorta med x. Kom ihåg att $x\neq 0$, men på väg mot noll - det är en viktig lärdom i gränsvärdeskalkylen.

Träna nu mycket på liknande tal, så du blir hemma med hantverket. Trevlig helg!

dr_lund skrev:

Ser bra ut. Det blir ett ändligt gränsvärde.

Anm Du kan frimodigt förkorta med x. Kom ihåg att $x\neq 0$, men på väg mot noll - det är en viktig lärdom i gränsvärdeskalkylen

Såklart! Borde jag insett, den här uppgiften tog slut på mig.