Hitta konjugatpartition i Sn, varför fungerar metoden?
Hej!
På en föreläsning visade min föreläsare följande "visuella" metod för att hitta en partition s.a. :
1. Skriv först upp på cykelform.
2. Skriv först upp på cykelform.
3.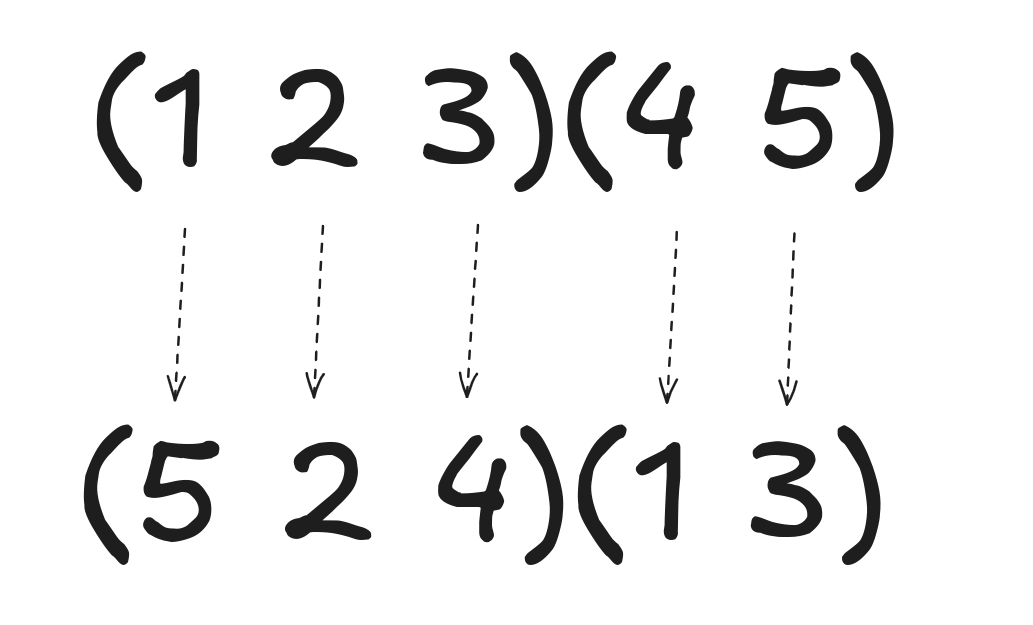
Skapa en bijektion enligt bilden, som visar ett exempel där = (1 2 3)(4 5), och = (5 2 4)(1 3), alltså resultatet blir =(1 5 3 4)(2).
Jag försöker förstå varför denna metod fungerar. Jag antar att man vill hitta att
. Men jag har svårt att "allmänt" överföra den bilden som min föreläsare ritade och skriva upp det hela i matematisk notation.
Kan någon hjälpa mig att förstå varför metoden fungerar? Tack så mycket! ⭐
Jag skulle tänka på som att du "översätter" till eller tvärtom. Mer precist så gäller det att permutationen ger oss samma resultat som om vi
- Först "byter namn" på talen genom att vi skickar
,
,
,
, och
.
Kalla detta namnbyte (dvs. bijektion) för ;
- Sedan utför vi permutationen . Eftersom 5 numer heter 1, och 3 numer heter 5, och så vidare, så blir detta som om vi utförde fast på ett annat språk, eller med andra namn.
- Sedan byter vi tillbaka namnen med , dvs.
,
,
,
, och
.
Summan av kardemumman är att vi får samma sak om vi utför som om vi först översätter till :s språk, utför , och sedan översätter tillbaka.
Om vi till exempel kollar på talet 4, så har vi att .
Om vi istället tittar på så skickas 4 först till 3 med , sedan skickas 3 till 1 med , och sist skickas 1 till 5 via , vilket sammantaget ger .
Anledningen till att vi gör först är för att skrivsättet brukar betyda att ett element skickas till , enligt komposition av funktioner. Vi hade också kunnat skriva om vi föredrar det.
Två permutationer och kallas konjugerade om det finns något sådant att .
Man kan visa följande:
Två permutationer och är konjugerade om och endast om de har samma cykelstruktur.
Samma cykelstruktur betyder att de har lika många 1-cykler, lika många 2-cykler, etc. Exempelvis har och samma cykelstruktur, men bägge har annan cykelstruktur än .
Det där var en väldigt bra och detaljerad förklaring. Tack så jättemycket!


