Hitta masscentrum

 

1. Jag har försökt beräkna med formel Xt = (m1x1+m2x2)/(m1+m2) men jag lärde mig att den var värdelös eftersom jag inte vet x1 eller x2 som avstånd till tyngdpunkten Xt 

 

2. Eftersom mitt förra detta försök misslyckades så gick jag vidare och försökte lösa med hjälp av att rita ned figuren och rita av vilka krafter som påverkar den i följande bild:

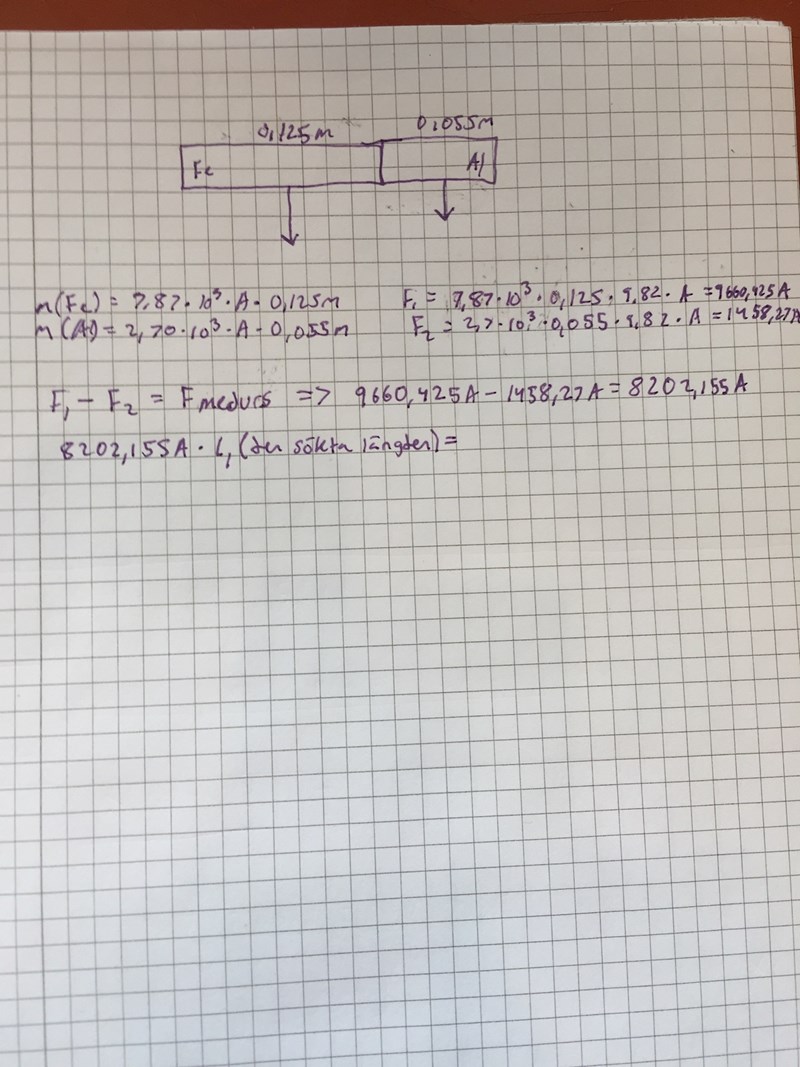
Här glömde jag skriva resulterande kraften som påverkar moturs mellan järn och alluminium bitarnas tyngdkraft

Oavsett så trodde jag att jag hade fått fram eller iallafall kommit nära en ekvation för att få fram längden från tyngdkraften med hjälp av den resulterande kraften från alla krafter medurs.

Däremot fastnade jag där = ligger i slutet av bilden eftersom jag inte vet storleken på krafter moturs och det känns som att man inte kan det , utan man måste ta reda på längden på något sätt men det förstår jag inte hur.

Med längden 1 på bilden i mitt försök så menar jag att änden av järnet är vridningsaxeln från den resulterande tyngdpunkten

 

Oavsett tänker jag att det måste finnas två normalkrafter med en från alluminiumet och en från järnet vilket tillsammans ger den resulterande kraften moturs som ligger i mitten mellan en del av järnet och hela delen av alluminiumet tillsammans, men där vet jag inte om jag tänker korrekt.

 

3.

Om jag skulle testa ett tredje försök så ligger det i tankeströmarna att man möjligtvis kan skriva en ekvation för hur stor andel massa ligger i järn änden och det samma gäller alluminium änden och sedan skriva t.ex (massa 1 * längd 1) = (massa 2 * hur långt från origo som den når alluminium änden)