Hitta max och minvärden
Jag blir förvirrad av en uppgift då de ger en funktion g(x,y)= x^2 -3x+3y^2 och sedan en avgränsning som inte innehåller hela funktionen: x^2+3y^2(mindre eller lika med) 9.
uppgiften är att bestämma största och minsta värde genom att undersöka randpunkter och inre kritiska punkter. Jag får maxvärde 18 och minvärde 0, men när jag skriver in detta i geogebra ser jag endast minvärde -9/4 och ingen maxvärde. Facit säger att maxvärde=18 minvärde=-9/4.
Hur ska jag tänka? 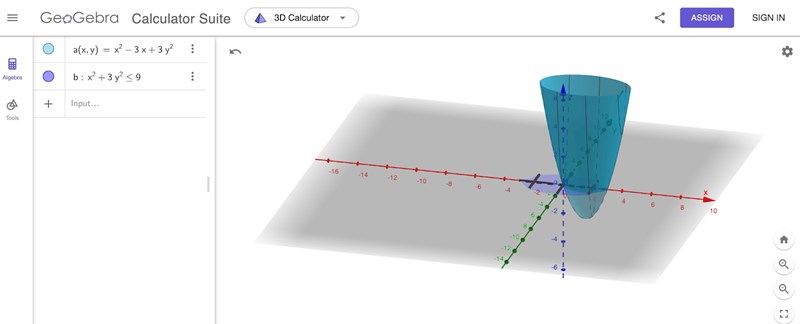
Du kan skriva g(x,y)=(x-3/2)^2+3y^2-9/4 varför minsta värde ses direkt, -9/4 i punken (3/2,0) som ligger i ditt definitionsområde. Eftersom g(x) är en kvadratisk form är det en "hängmatta" i alla riktningar och du finner största värdet på randen. I det här fallet i punkten (-3,0). Det ligger logik i det med, då "hängmattans" minimum var (3/2,0) och formen är kvadratisk med maximal tillväxt i ett av leden. Om du ser på din bild ser du att (-3,0) ligger "längst bort" från minimum och därmed antas max där. Men! parameterisering av randen är att rekommendera, du får då en funktion av en variabel.
Med parametrisering av randen får jag maxvärdet 18 precis som facit men jag kan inte räkna fram minvärdet -9/4. Jag tänker att minvärdet fås i en inre kritisk punkt eftersom de värden jag får med parametrisering av randen är 0 och 18. Jag hittar en kritisk punkt (3/2,0) men detta ger mig 9/4 om jag sätter in punkterna i x^2+3y^2.
Nu ser jag att jag får -9/4 om jag använder funktionen g(x,y) och sätter in punkterna (3/2,0). Jag blandar ihop när jag borde använda funktionen och områdsbegränsningen
Gulnigar_yeye skrev:Med parametrisering av randen får jag maxvärdet 18 precis som facit men jag kan inte räkna fram minvärdet -9/4. Jag tänker att minvärdet fås i en inre kritisk punkt eftersom de värden jag får med parametrisering av randen är 0 och 18. Jag hittar en kritisk punkt (3/2,0) men detta ger mig 9/4 om jag sätter in punkterna i x^2+3y^2.
Nu ser jag att jag får -9/4 om jag använder funktionen g(x,y) och sätter in punkterna (3/2,0). Jag blandar ihop när jag borde använda funktionen och områdsbegränsningen
Övning ger färdighet.
Just denna funktion är en '2-dim variant' på en parabel och då ser man direkt att minimum är -9/4 vilket antas när kvadraterna är båda 0 vilket de är i punken (3/2,0). De är ungefär som att du skulle bestämma minimum för y=(x-1)^2-1. Du ser direkt att minimum är -1 och det antas för x=1.


