Hitta maximum och minimum till f(x, y)

Hej!

Jag har fastnat på denna uppgift:

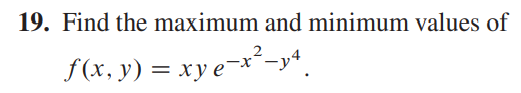
För räknade jag ut respektive partiell derivata:

$f_{x} (x, y) = y e^{- x^{2} - y^{4}} (1 - 2 x^{2}) f_{x} (x . y) = 0 y = 0 e l l e r x = \pm \frac{1}{\sqrt{2}} f_{y} (x, y) = x e^{- x^{2} - y^{4}} (1 - 4 y^{4}) f_{y} (x, y) = 0 y = \frac{1}{\sqrt[4]{4}} e l l e r x = 0$

Detta ger kritiska punkterna $(- \frac{1}{\sqrt{2}}, 0), (\frac{1}{\sqrt{2}}, 0) o c h (0, \frac{1}{\sqrt[4]{4}})$

Hur ska man göra nu? Det känns lite komplicerat att räkna ut andraderivatan, så det kanske är fel

Du har gjort fel med de kritiska punkterna. I en kritisk punkt ska båda partiella derivator vara 0.

Så exempelvis (0,0) är en kritisk punkt men ingen av de punkter du angivit är det.

När du fått kritiska punkterna rätt är det rimligt att i nästa steg evaluera funktionen i de punkterna.

Ytterligare en grej, det ser för dumt ut när du skriver fjärde roten ur fyra.+/- roten ur två får du göra där.

Smutsmunnen skrev:
Du har gjort fel med de kritiska punkterna. I en kritisk punkt ska båda partiella derivator vara 0.

Så exempelvis (0,0) är en kritisk punkt men ingen av de punkter du angivit är det.

När du fått kritiska punkterna rätt är det rimligt att i nästa steg evaluera funktionen i de punkterna.

Juste! Tack, jag löste den nu! :)

Svara Avbryt

Visa senaste svar