Hitta primitiv
Hej
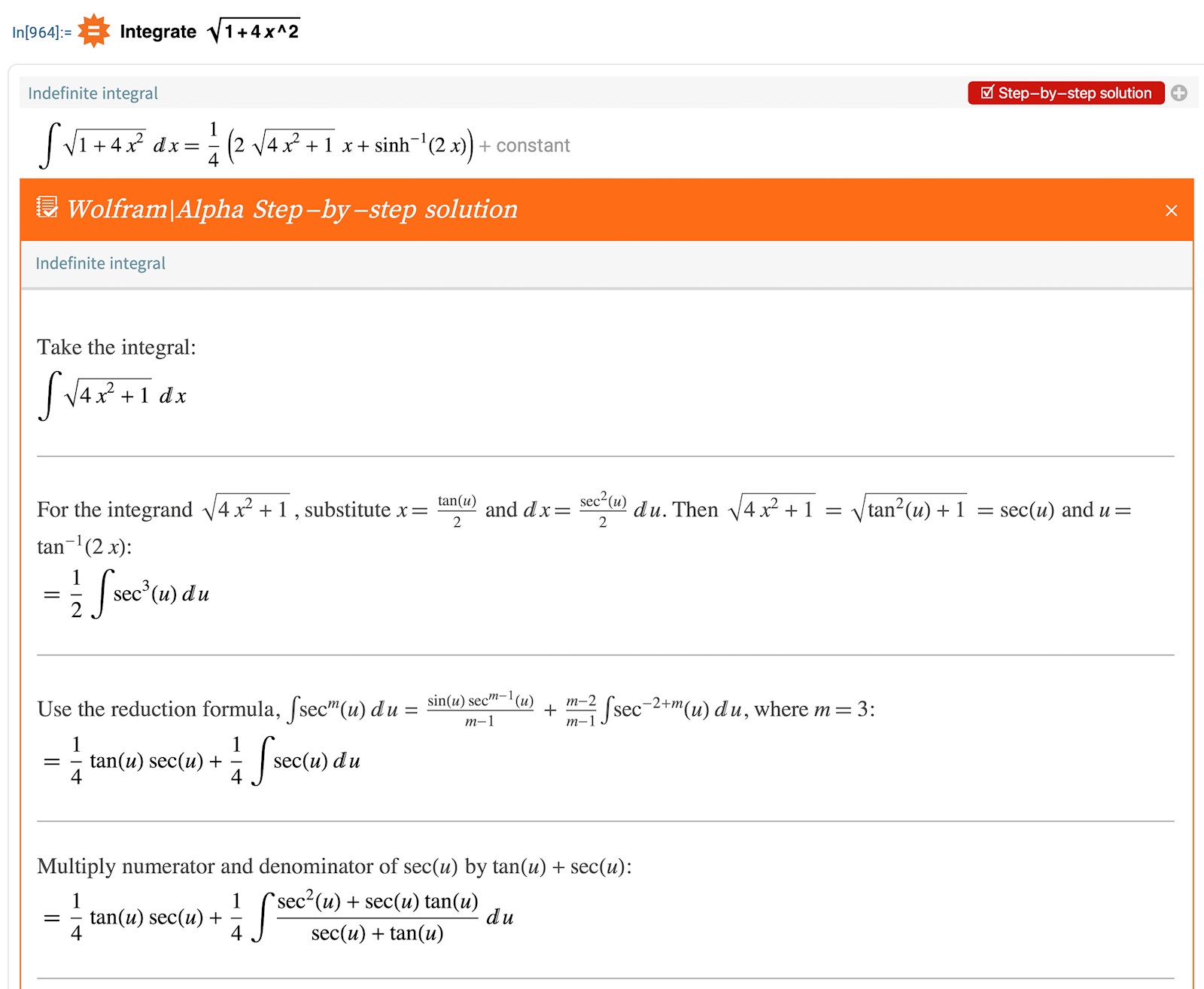
Hur hittar man primitiv till
Jag har börjat med att skriva 2x = tanθ och kommit fram till .
Jag frågade Wolfram och det verkar inte vara "glasklart" om man inte har en reduktionsformel, fast vem vet om Wolfram väljer den enklaste vägen.
I många läroböcker är prim.fkn. till sec(x) en standardintegral, men här visas hela vägen.


Om man inte vil använda "the reduction formula" kan du använda partiell integration. Kanske mindre diffust.
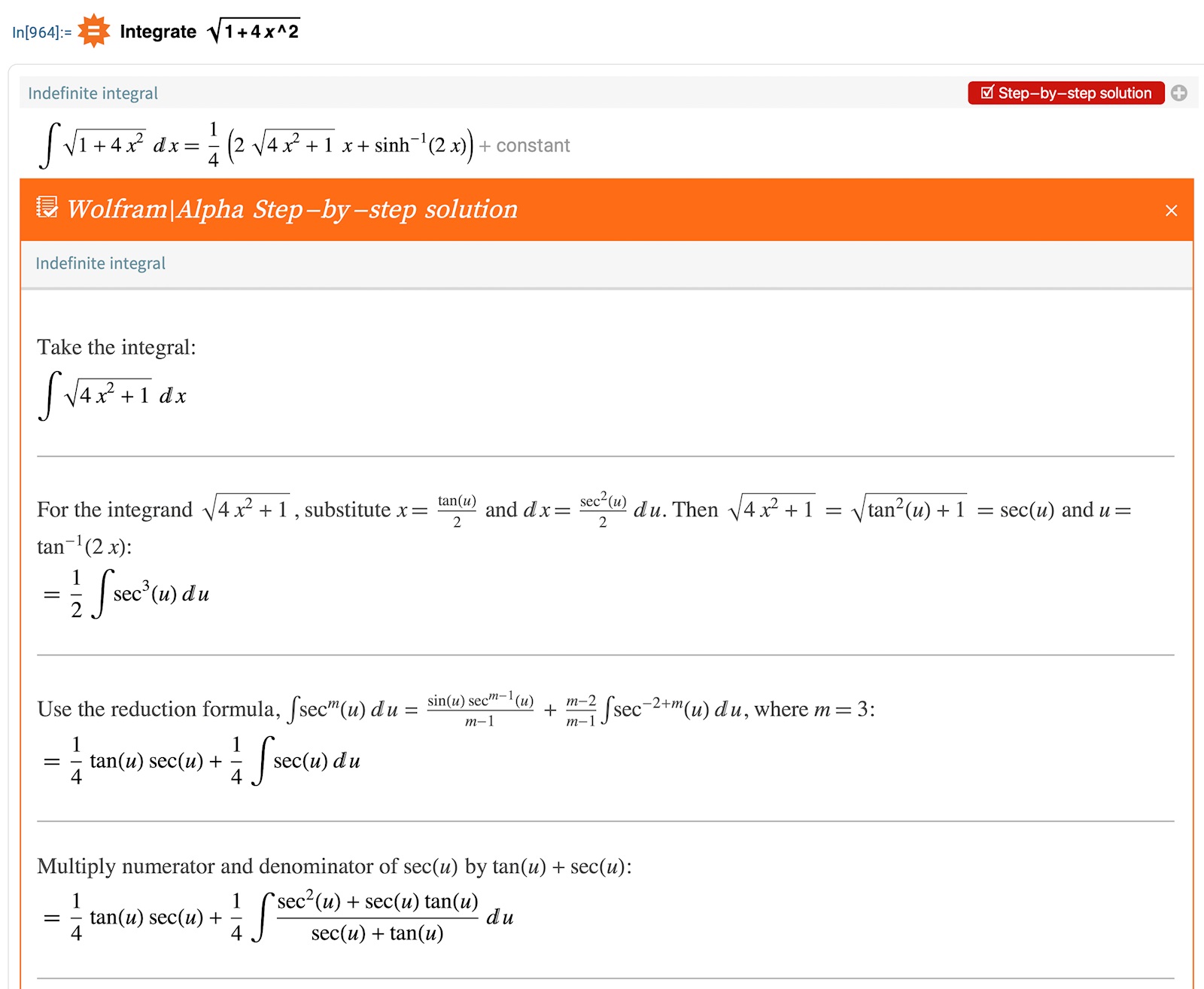
Trinity2 skrev:Jag frågade Wolfram och det verkar inte vara "glasklart" om man inte har en reduktionsformel, fast vem vet om Wolfram väljer den enklaste vägen.
I många läroböcker är prim.fkn. till sec(x) en standardintegral, men här visas hela vägen.
Det står inget om den funktionen i min lärobok så jag antar att det måste finnas en annan väg att lösa primitiven. Annars borde jag kanske nu lära mig den
Gunnar_ skrev:Om man inte vil använda "the reduction formula" kan du använda partiell integration. Kanske mindre diffust.
Hur då tänkte du? Du kanske får till det, men jag får en mer och mer krånglig integrand..
Studera beviset för reduktionsformeln. Man separaerar i fallet med sec^3 i två delar sec^2 och sec där prim.fkn. till sec^2 är tan och sedan får man tillbaka sec^3 igen och får en integralekvation

Säg till om det är oklart så kan vi lösa det i specialfallet n=3 så kanske det blir lite klarare.
Integranden innehåller en udda potens av cosinus, nämligen cos-3θ. Standardmetoden som brukar läras ut är då variabelbytet t = sin θ, dt = cos θ dθ.
,
vilket sedan löses m.h.a. partialbråksuppdelning.
Btw: Om man känner till hyperboliska funktioner, så kan ursprungsintegralen lösas mycket snabbare och på ett enklare sätt tack vare hyperboliska ettan .
Det återstår att invertera sinh t (det blir en andragradsekvation som behöver lösas) för att kunna gå tillbaka till x.