Hitta rötter till komplex ekvation

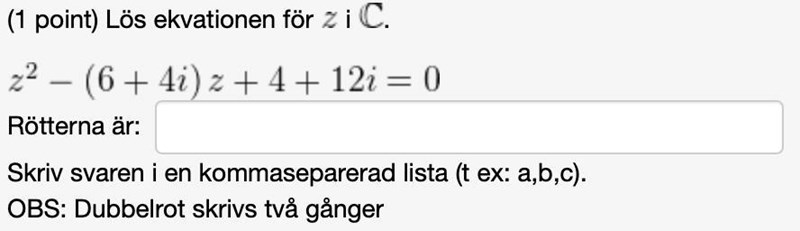
Började med att skriva z=a+bi, insåg sedan att ekvationen skulle bli rätt jobbig att lösa. Så undrar om det finns något enkelt snabbt sätt att lösa ekvationen?

Update: Testade att utveckla, men det blev fortfarande fel.

Den går ganska lätt att lösa med kvadratkomplettering.

SvanteR skrev:
Den går ganska lätt att lösa med kvadratkomplettering.

$(z - {(3 + 2 i))}^{2} - {(3 + 2 i)}^{2} + 4 + 12 i = 0 (z - {(3 + 2 i))}^{2} - (9 + 12 i - 4) + 4 + 12 i = 0 (z - {(3 + 2 i))}^{2} - 1 = 0 z = 3 + 2 i \pm 1 z = 4 + 2 i e l l e r z = 2 + 2 i$

Tack för hjälpen!

Svara

Visa senaste svar