Hitta trianglarna

Triangelns vinkelsumma ger:

$A+B+C=180^\circ$

$B+2B=180^\circ$

$B=60^\circ$

Sinussatsen ger därefter:

$\dfrac{a}{\sin(A)}=\dfrac{b}{\sin(B)}=\dfrac{c}{\sin(C)}$

ur vilket vi får:

$a=\dfrac{\sin(A)}{\sin(B)}\cdot b$

$c=\dfrac{\sin(C)}{\sin(B)}\cdot b$

Areasatsen ger sedan att arean $A_T$ kan uttryckas som:

$A_T=\dfrac{ac}{2}\cdot\sin\left(B\right)$

Insättning av uttrycken för $a$ och $c$ från sinussatsen ger:

$A_T=\dfrac{\sin(A)}{\sin(B)}\cdot b\cdot\dfrac{\sin(C)}{\sin(B)}\cdot b\cdot\dfrac{\sin(B)}{2}$

$A_T=\sin\left(A\right)\sin\left(C\right)\cdot\dfrac{b^2}{2\sin(B)}$

Då $b=2\sqrt{6}(\sqrt{3}-1)$ och $B=60^\circ$ erhålls:

$A_T=\sin\left(A\right)\sin\left(C\right)\cdot\dfrac{(2\sqrt{6}(\sqrt{3}-1))^2}{2\sin(60^\circ)}$

$A_T=\sin\left(A\right)\sin\left(C\right)\cdot\dfrac{4\cdot6(3-2\sqrt{3}+1)}{\sqrt{3}}$

$A_T=\sin\left(A\right)\sin\left(C\right)\cdot\dfrac{48(2-\sqrt{3})}{\sqrt{3}}$

Då ett uttryck för arean, $A_T=4\sqrt{3}(2-\sqrt{3})$, är känt får vi:

$\sin\left(A\right)\sin\left(C\right)\cdot\dfrac{48(2-\sqrt{3})}{\sqrt{3}}=4\sqrt{3}\left(2-\sqrt{3}\right)$

$\sin\left(A\right)\sin\left(C\right)\cdot48\left(2-\sqrt{3}\right)=4\cdot 3\left(2-\sqrt{3}\right)$

$\sin\left(A\right)\sin\left(C\right)=\dfrac{12}{48}=\dfrac{1}{4}$

Det finns en färdig formel för att omvandla en produkt av typen $\sin(A)\sin(C)$ till en summa, men låt oss härleda detta bara för kul skull:

Additions- och subtraktionsformlerna för cosinus ger:

$\cos(A-C)=\cos(A)\cos(C)+\sin(A)\sin(C)$

$\cos(A+C)=\cos(A)\cos(C)-\sin(A)\sin(C)$

Vi ser att differensen $\cos(A-C)-\cos(A+C)$ tar ut cosinustermerna:

$\cos(A-C)-\cos(A+C)=2\sin(A)\sin(C)$

Delas båda led med två fås:

$\sin\left(A\right)\sin\left(C\right)=\dfrac{\cos(A-C)-\cos(A+C)}{2}$

Om vi utnyttjar detta i vår ekvation erhålls:

$\dfrac{\cos(A-C)-\cos(A+C)}{2}=\dfrac{1}{4}$

$\cos\left(A-C\right)-\cos\left(2B\right)=\dfrac{1}{2}$

$\cos\left(A-C\right)-\cos\left(120^\circ\right)=\dfrac{1}{2}$

$\cos\left(A-C\right)=\dfrac{1}{2}+\cos\left(120^\circ\right)=\dfrac{1}{2}-\dfrac{1}{2}$

Således är
$\cos\left(A-C\right)=0$

vilket ger oss antingen att $A-C=90^\circ\Rightarrow A=90^\circ+C$ eller $C-A=90^\circ\Rightarrow C=90^\circ+A$

Insättes detta i $A+C=2B$ kan vi lösa ut för $A$ och $C$:

$90^\circ+C+C=2B$

$90^\circ+2C=120$

$C=15^\circ$

$A=90^\circ+C=105^\circ$

Den andra varianten, $C-A=90^\circ$, ger sedan $A=15^\circ$ och $C=105^\circ$.

De möjliga trianglarna har alltså vinklarna $A=15^\circ$, $B=60^\circ$ och $C=105^\circ$ eller $A=105^\circ$, $B=60^\circ$ och $C=15^\circ$. Med de tidigare uttrycken framtagna med hjälp av sinussatsen är det sedan ganska enkelt att ta fram längderna på sidorna $a$ och $c$:

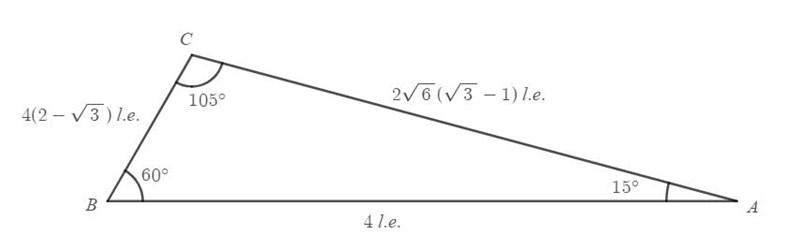
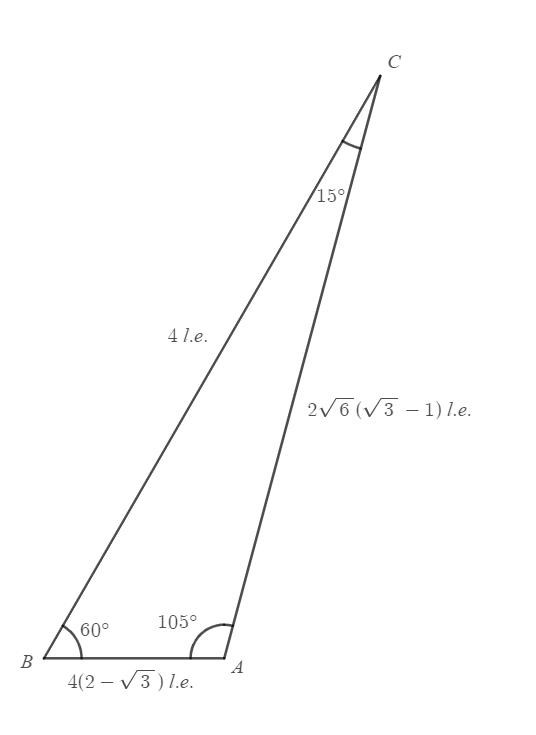
Observera att trianglarna bara är speglingar av varandra, men med benämningarna $A$ och $C$ utbytta.