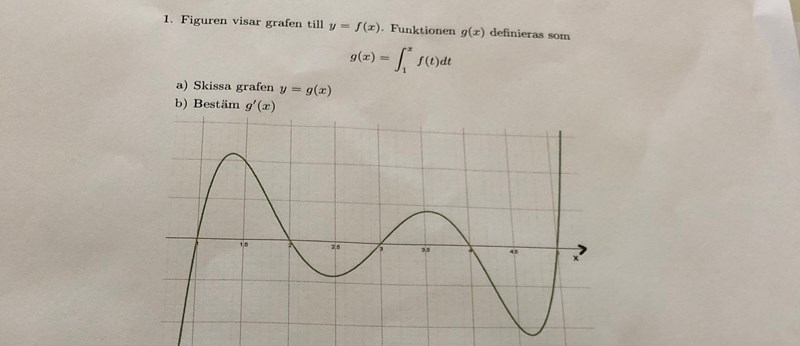
Skissa graf och bestämma derivata
Jag fattar inte hur jag ska lösa denna uppgift skulle någon kunna hjälpa mig?!!
Rubrik ändrad från "Hjäällpp" till nuvarande. Det står i Pluggakutens regler att trådens rubrik ska beskriva trådens innehåll. /Smutstvätt, moderator
Är 't' x-axeln?
Ja (t) står för X
Hani skrev:Ja (t) står för X
Vad är enheterna då?
Jaha, du ska bara skissa y = g(x). Integral betyder i princip arean mellan grafen och x-axeln. Som du ser så Ökar arean till en början, sen minskar den, sen ökar den lika mycket och sen minskar den till noll. Sen ser det ut som att den blir väldigt stor igen. Sen minskar den. Det upprepas
Kan du skissa det?
Jag förstår att integraler är area men jag vet inte hur jag ska skissa den
Skriv en vettig rubrik som beskriver innehållet i tråden. Det står i Pluggakutens regler. /Smutstvätt, moderator
Iridiumjon skrev:Är 't' x-axeln?
Vad menas med den frågan?
Vart kommer uppgiften ifrån?
Det är en klassuppgift som vi fick under matte 3c lektionen
Iridiumjon skrev:Jaha, du ska bara skissa y = g(x). Integral betyder i princip arean mellan grafen och x-axeln. Som du ser så Ökar arean till en början, sen minskar den, sen ökar den lika mycket och sen minskar den till noll. Sen ser det ut som att den blir väldigt stor igen. Sen minskar den. Det upprepas
Kan du skissa det?
Skulle du kunna hjälpa mig skissa den
Skulle du kunna hjälpa mig skissa den
Försök själv istället! Det står i Pluggakutens regler att du skall visa hur du har försökt och hur långt du har kommit. /moderator
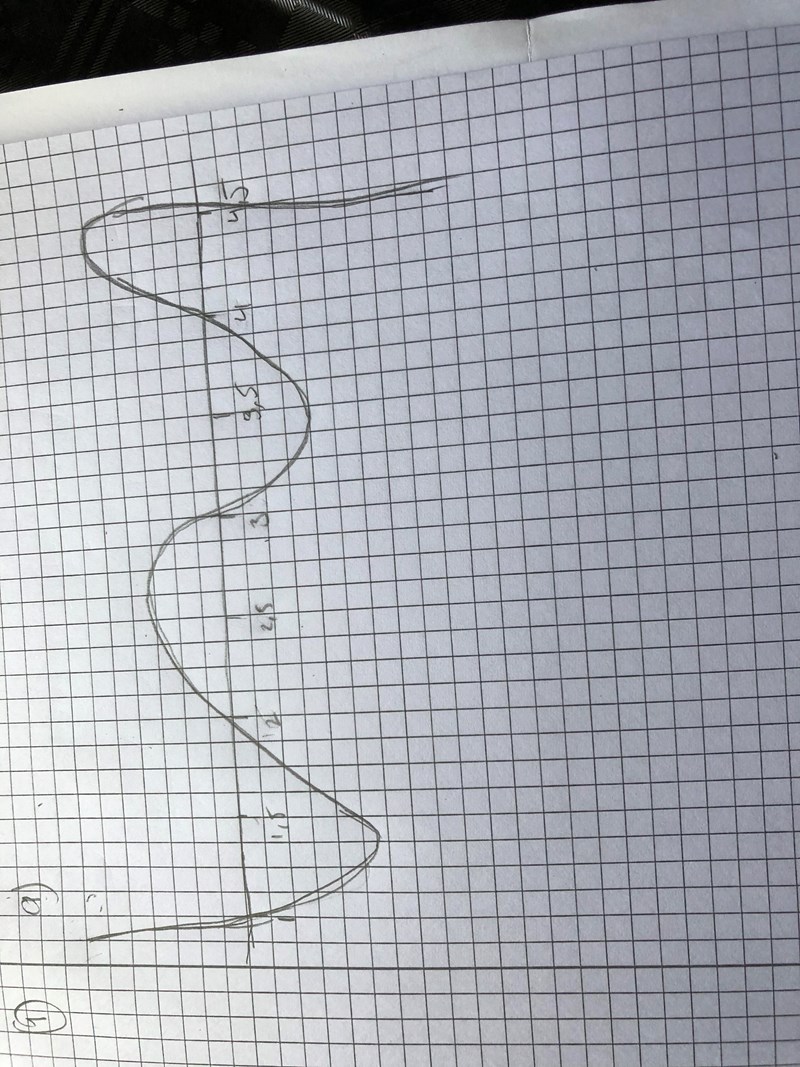
Integralen börjar med värdet 0 när x=1 och ökar ganska snabbt (och snabbare och snabbare) tills x=1,6 ungefär, sedan fortsätter integralens värde att öka men långsammare, tills den når sitt största värde är x=2... Fortsätt själv och lägg upp biden här!
Hani skrev:
Ser det rätt ut?
Ser det rätt ut?
Nej. Förutom att du har lagt in bilden på fel håll, vilket gör att jag känner mig så här

så visar din graf ett negativt värde på integralen i intervallet 1<x<2, och det är fel.
Hahaha oj förlåt, hur blir det då?
Iridiumjon skrev:Jaha, du ska bara skissa y = g(x). Integral betyder i princip arean mellan grafen och x-axeln. Som du ser så Ökar arean till en början, sen minskar den, sen ökar den lika mycket och sen minskar den till noll. Sen ser det ut som att den blir väldigt stor igen. Sen minskar den. Det upprepas
Kan du skissa det?
Som Iridiumjon skrev redan i går eftermiddag. Eller läs mitt inlägg tidigare idag:
Integralen börjar med värdet 0 när x=1 och ökar ganska snabbt (och snabbare och snabbare) tills x=1,6 ungefär, sedan fortsätter integralens värde att öka men långsammare, tills den når sitt största värde är x=2... Fortsätt själv och lägg upp biden här
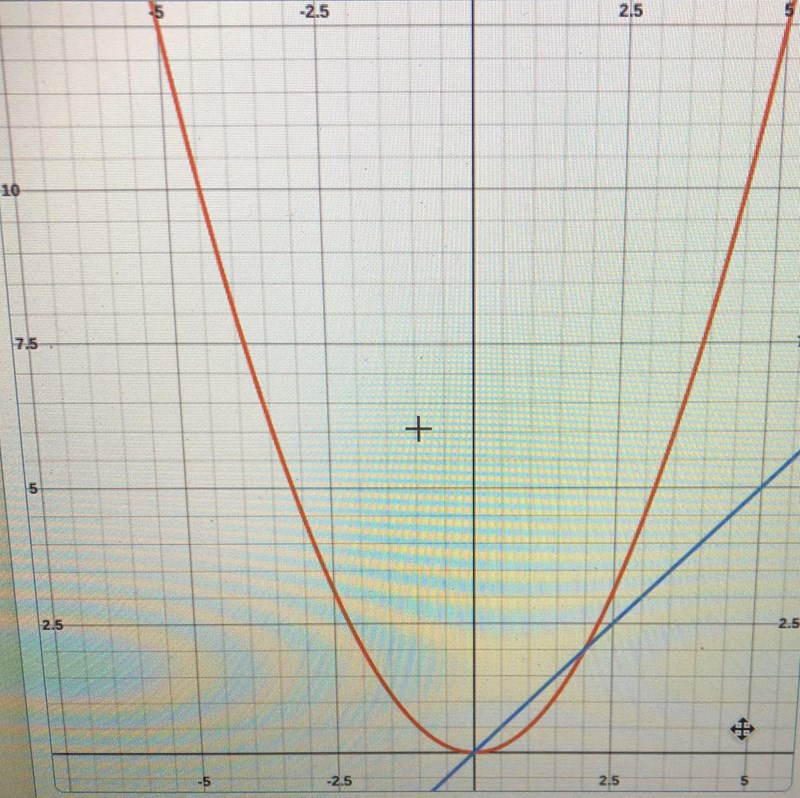
ÄR detta rätt
Hani skrev:
ÄR detta rätt
Nej. Vilken graf menar du? Du har en rät och en andragradsfunktion. Båda är fel. Båda ökar bara i värde hela tiden, men integralen blir ju noll efter ett tag.
Iridiumjon skrev:Hani skrev:
ÄR detta rätt
Nej. Vilken graf menar du? Du har en rät och en andragradsfunktion. Båda är fel. Båda ökar bara i värde hela tiden, men integralen blir ju noll efter ett tag.
jag syftade på andragradsfunktionen. Men hur blir det då?
Hani skrev:
ÄR detta rätt
På vilket sätt har de här kurvorna något samband med den här uppgiften, menar du? Vad betyder den blå kurvan? Vad betyder den röda kurvan?
Kan du försöka rita en graf som symboliserar hur vita området mellan grafen och x-axeln ökar respektive minskar?
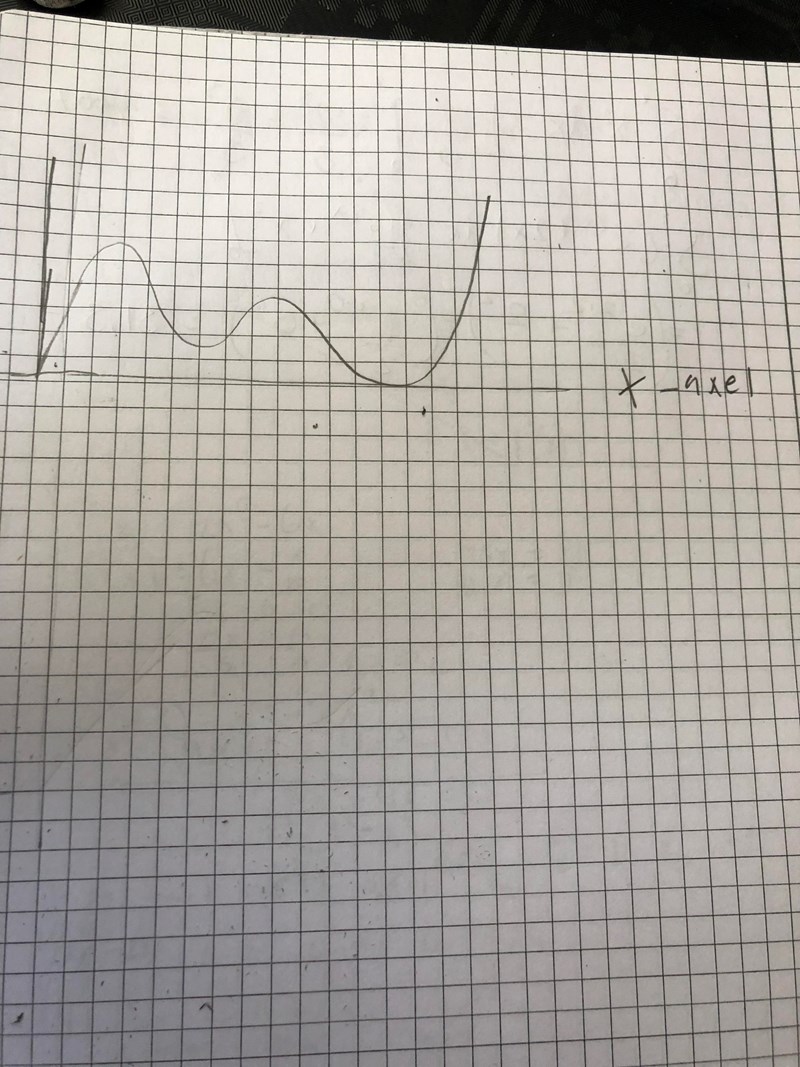 menar du såhär?
menar du såhär?
Andra toppen borde vara lika hög som den första, annars ser det bra ut.
Hani skrev:
menar du såhär?
Bra!
Enda som är fel nu är, som Laguna sa, att andra toppen ska vara lika hög som första.
På B uppgiften ska jag skriva g'(x)= ∫ 1x f(t 2/2) dt
Hani skrev:På B uppgiften ska jag skriva g'(x)= ∫ 1x f(t 2/2) dt
Du ska bestämma g'(x). Vad är derivatan av en integral?
(Var fick du t2/2 ifrån?)
Laguna skrev:Hani skrev:På B uppgiften ska jag skriva g'(x)= ∫ 1x f(t 2/2) dt
Du ska bestämma g'(x). Vad är derivatan av en integral?
(Var fick du t2/2 ifrån?)
Jag stoppade in 1 i f(t) och sedan deriverade
Hani skrev:Laguna skrev:Hani skrev:På B uppgiften ska jag skriva g'(x)= ∫ 1x f(t 2/2) dt
Du ska bestämma g'(x). Vad är derivatan av en integral?
(Var fick du t2/2 ifrån?)
Jag stoppade in 1 i f(t) och sedan deriverade
Det där förstod jag tyvärr inte alls. Kan du utveckla?
Deriverar du en integral kommer du tillbaka till "ursprungsfunktionen".
Iridiumjon skrev:Deriverar du en integral kommer du tillbaka till "ursprungsfunktionen".
Aa exakt hur kan jag göra då?
hur kan man derivera en integral
Hani skrev:hur kan man derivera en integral
Är du med på att g är integralen av f?
Hani skrev:hur kan man derivera en integral
Då får du tillbaka funktionen du började med. F'(x)=f(x). Det kallas integralkalkylens huvudsats.
Om jag har uppfattat detta rätt så går integralen tillbacka till det ursprungliga det vill säga g( x)= ∫ x1 f(t)dt eller?
Nej, inte riktigt. Du skall inte ha med något integraltecken utan använda dig av skrivsättet F(x). Vad blir g(x) skrivet på det sättet?
jag förstår inte riktigt hur g(x) blur då
Är der rätt?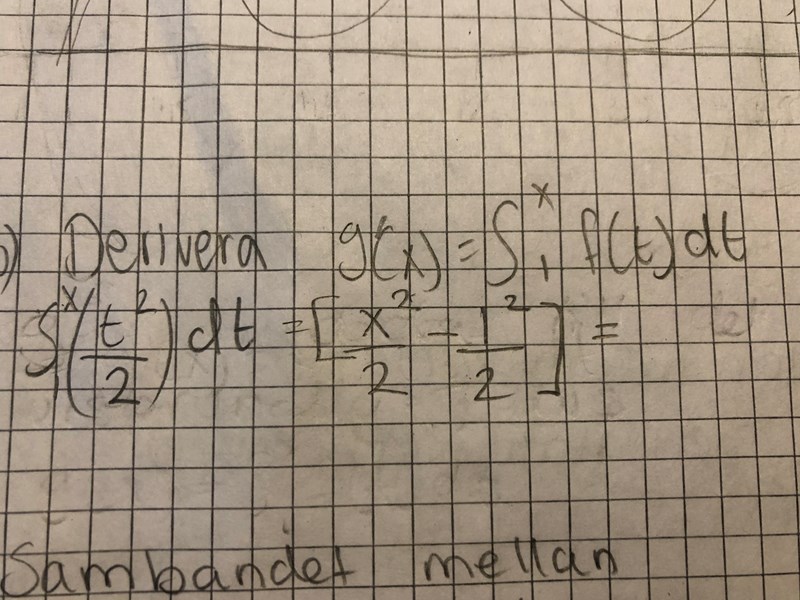
Utnyttja att . Vad blir det när du deriverar g(x)?
blir det då g(x)= [F(t 2/2 )] x1 = ( x 2 /2 - 1 2/2)
Hani skrev:blir det då g(x)= [F(t 2/2 )] x1 = ( x 2 /2 - 1 2/2)
Vad gör du nu? Jag förstår inte vad det är du gör, du behöver förklara tydligare. När du vet att g(x)=F(x)-F(1) har du ju blivit av med variabeln t. Vad är det du kvadrerar?