Hjälp Madam Chef Ingenjör

Det är en 4 poäng fråga i den svåraste del av tentan, vad måste man säga här? Jag tänkte att det är bara att projicera två oberoende vektorer som spänner upp ett plan? Vad annars måste man skriva? Vad måste man inse här?
(... känns som jag vill gå på terapi efter detta fråga)
Det räcker faktiskt! Välj två oberoende vektorer i R^3, a och b. Efter knapptryckningarna får vi ut och . Om vi har tur, kommer och . Då har vi två oberoende vektorer i det tvådimensionella delrummet, och kan därmed bestämma vilket delrummet är. Troligtvis har Madam Chefsingenjör inte en sådan tur, och då behöver vi rita lite:
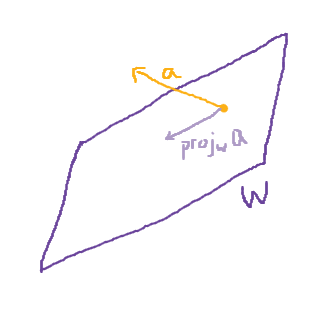
Ledtråd: Vad händer nu om vi tar ?
Morgon smutso!
Alltså trycker hon två gånger på knappet (med två oberoende vektorer) får hon en plan (två oberoende vektorer i en tvådimensionell rum). Varför måste vi grannschmitta saken? Vad är dem efter? Varför behöver vi en ortogonal form för delrummet?
Ja, vi stoppar in en vektor a och trycker på knappen. Det finns då två möjligheter för vad som kan hända:
- a ligger redan i planet W, och projiceras då på sig själv. Då måste vi ha en till vektor för att bestämma W.
- a ligger inte i planet W, och då kan vi bestämma en normalvektor till planet, klart.
Om vi valt två i R^3 oberoende vektorer, kommer de att bli oberoende i W också. Då vet vi att vi, i ett sämsta-fallscenario, har två vektorer i planet, som vi kan kryssa och använda för att bestämma W.
Måste vi ta hänsyn till fallet där hon plockar en vektor i W och projicerar den tillbaka? Det är ju en kvinna som är chef, hur skull hon vara så negligent :D?
Tror du att vi måste skriva planetsekvation i detta uppgiften?
Vad för helveuuute vill dem?
Hon vet ju inte vad W är, ju! Det är en statistisk möjlighet att hon råkar välja en vektor i W. Så ja, det måste vi.
Nej, det går inte eftersom vi inte vet vad projiceringen gör.
De vill att du ska argumentera för eller emot om det går att ta reda på vilket planet är.
Nja... det är klart att det gör ju, vi har två projektioner kvar. Även med ett (tack din färgglad och vacker figur) kan vi dra en normal. Det är en 4-poängare, kan du tro det?
Tack för att du uppskattar mina kråkfotsskisser!



