Hjälp med att visualisera en uppgift

Förslag: Använd enhetscirkeln.

Börja med att rita en vinkel v i första kvadranten och markera dess sinusvärde. Rita även vinkeln 270-v (hamnar då i tredje kvadranten) och markera dess cosinusvärde. Du ser då sambandet.

Gör sedan samma sak för övriga kvadranter.

Hej Börje!

Nu gjorde jag inte exakt som du instruerade. Ser det helt galet ut eller?: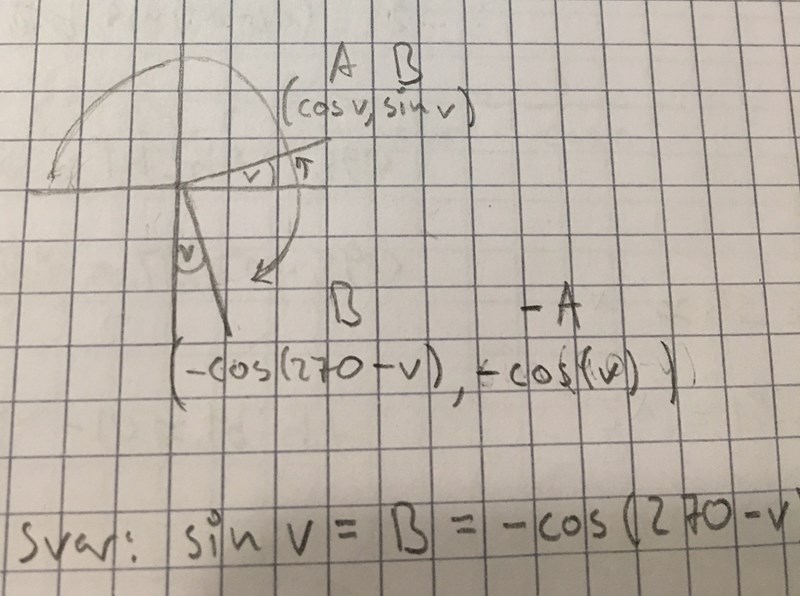

Ja, du har ritat 270° + v.

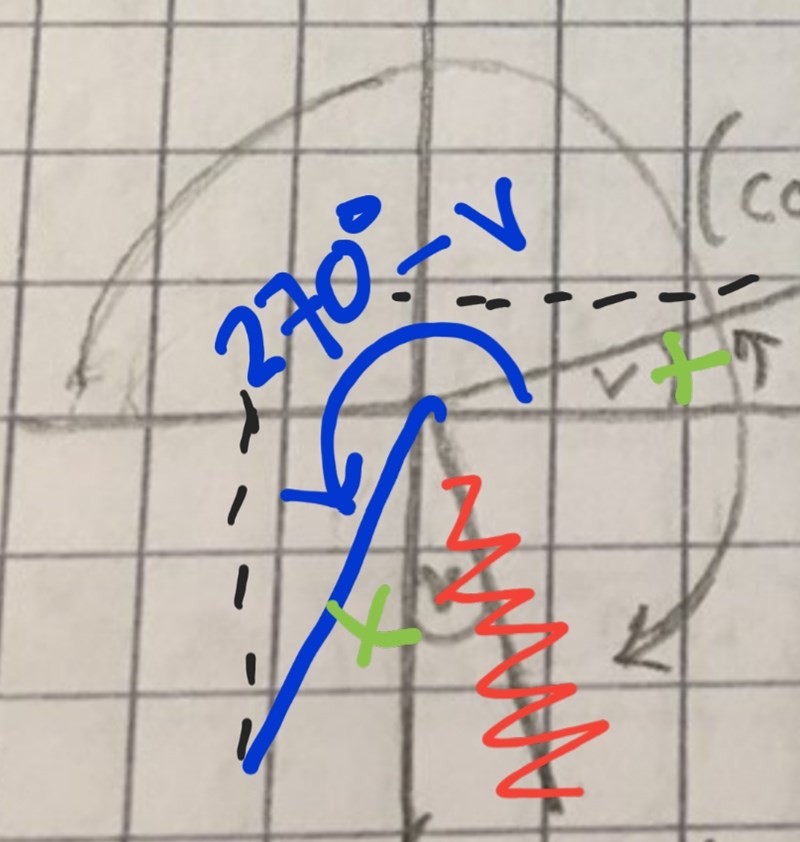
Jag har markerat 270° - v i figuren nedan.

Du ska alltså gå fram (moturs) 270 grader, sedan tillbaka (medurs) v grader.

• Om v ligger i första kvadranten så kommer 270° - v att hamna i tredje kvadranten.
• Om v ligger i andra kvadranten så kommer även 270° - v att hamna i andra kvadranten.
• Om v ligger i tredje kvadranten så kommer 270° - v att hamna i första kvadranten.
• Om v ligger i fjärde kvadranten så kommer även 270° - v att hamna i fjärde kvadranten.

Hej!

Okej, då får jag koordinaterna för v till (cos v, sin v) = (a,b) och koordinaterna för 270-v till (-sin(270-v),-cos(270-v)) = (-b,-a). Som en parantes fick jag fram detta genom att testa mig fram, t.ex. sin 10 = -cos(270-10).

Jag antar minustecknet framför cos:et i (-sin(270-v),-cos(270-v)) är detsamma som minustecknet framför a:et i (-b,-a)? Så man skulle kunna skriva -(cos(270-v)) men har valt att skriva det som -cos(270-v)?

Den visuella kopplingen jag gör är att sin v i y-led är lika positiv som cos(270-v) är negativ i x-led.

Jag har försökt mig på att visa sambandet med algebra:

$$\begin{gathered} \sin v = -\cos (270-v) \\ Använd substraktionssatsen \cos (u-v)=\cos u \cos v + \sin u \sin v på HL \\ \sin v = -(\cos 270\cos v+\sin 270\sin v) \\ \sin v = -\cos 270\cos v-\sin 270\sin v) \\ \sin v = -(0°)\cos v-(-1°)\sin v \\ \sin v = \sin v \end{gathered}$$

Blev det bättre nu?                                      

Hej. v är en vinkel och ingen punkt, så det blir fel att skriva att v har koordinaterna (cos v, sin v) = (a,b).

-------------

Du skrev att du ville ha hjälp att visualisera sambandet och det tycker jag att du har lyckats med här:

Krissehiss skrev :

... 

Den visuella kopplingen jag gör är att sin v i y-led är lika positiv som cos(270-v) är negativ i x-led.

 ...           

Dvs sin(v) = -cos(270°-v).

Gör gärna samma övning med v i andra, tredje och fjärde kvadranten.

Detta dels för att övertyga dig om att sambandet stämmer överallt, dels för att träna på att rita in de två vinklarna v och 270°-v i lite mer komplicerade fall.

-----------

Vad gäller härledningen av sambandet på slutet så ser devt bra ut, förutom att gradsymbolen efter siffervärdena 0 och -1 ska bort.