Hjärnfrys 2 under integrering 1/(sin9x)

Rotuttrycket $\sqrt{1-t^2}$ är tyvärr inte till någon hjälp här. För att lösa ett sådant behöver man göra en sinus eller cosinussubstitution, och då är man tillbaka där vi började.

I det här fallet skulle jag rekommendera den ganska luriga halvvinkeltangens-subsitutionen:

https://en.wikipedia.org/wiki/Tangent_half-angle_substitution

 hahaha vad lovande!

"The world's sneakiest substitution is undoubtedly" this technique."

Tan-halva-tricket är ett väldigt generellt trick så är rätt värt att lära sig det.

Just 1/sin-integralen är även angripsbar med ett annat trick där man förllänger det rationella uttrycket med en faktor sin(x) vars syfte är att möjliggöra en annan trigonometriskt substitution. 

$\int \frac{dx}{\sin(x)} = \int \frac{\sin (x)dx}{\sin^2 (x)} = \int \frac{\sin(x)}{1 - \cos^2(x)}$

Och därefter med substitutionen $y = \cos x$

$\int \frac{dx}{\sin(x)} = -\int \frac{dy}{1 - y^2}$

Följt av partialbråksuppdelning. Detta trick kan anpassas för en klass av på vissa trigonometriska trationella uttryck men fungerar inte på alla medan tan-halva-gör det. 

Ett annat brute-force-trick man kan göra är att skriva om sina trigonometriska funktioner på komplex form

$\cos(x) = \frac{e^{ix} + e^{-ix}}{2}$

$\sin(x) = \frac{e^{ix} - e^{-ix}}{2i}$

och substituera för $z = e^{ix}$ men det är något involverat för det mesta. 

AlvinB skrev:

Rotuttrycket $\sqrt{1-t^2}$ är tyvärr inte till någon hjälp här. För att lösa ett sådant behöver man göra en sinus eller cosinussubstitution, och då är man tillbaka där vi började.

I det här fallet skulle jag rekommendera den ganska luriga halvvinkeltangens-subsitutionen:

https://en.wikipedia.org/wiki/Tangent_half-angle_substitution

Jag har undersökt lite grand och...

Jag ska försöka BrainysOctopus  metod också, men just nu fastnade jag på den här 9:an. Vad gör jag med 9an?

Alltså:

$$\begin{gathered} \int \frac{dx}{\sin \left(9x\right)} \\ \left[\begin{array}{c}x=2arc\tan \left(t\right)\\ t=\tan \left(\frac{x}{2}\right)\\ dx=\frac{2}{1+t^2}dt\end{array}\right] \end{gathered}$$

So far so good, men : $\sin (9·2 arc\tan t)=\sin (2· 9 arc\tan t)$

$2\sin (9arc\tan t)\cos (9arc\tan t)=2 \frac{9·t}{\sqrt{1+t^2}}\frac{9·1}{\sqrt{1+t^2}}=\frac{2·9^2·t}{1+t^2}$

$$\begin{gathered} \int \frac{dx}{\sin \left(9x\right)} \iff \int \frac{\left(\frac{2}{1+t^2}\right)}{\left(\frac{2·9^2·t}{1+t^2}\right)}dt=\int \frac{1}{9^{2}t}dt \\ = \ln \left|9^{2}t\right|= \ln \left|9^2\left(\tan \frac{x}{2}\right)\right| \end{gathered}$$

Som inte är rätt svar tror jag.

Sätt

t = tan(9x/2)

Pröva att göra en substitution $s=9x$ innan halvvinkelsubstitutuionen så blir du av med nian. :-)

SeriousCephalopod skrev:

Tan-halva-tricket är ett väldigt generellt trick så är rätt värt att lära sig det.

Just 1/sin-integralen är även angripsbar med ett annat trick där man förllänger det rationella uttrycket med en faktor sin(x) vars syfte är att möjliggöra en annan trigonometriskt substitution. 

$\int \frac{dx}{\sin(x)} = \int \frac{\sin (x)dx}{\sin^2 (x)} = \int \frac{\sin(x)}{1 - \cos^2(x)}$

Och därefter med substitutionen $y = \cos x$

$\int \frac{dx}{\sin(x)} = -\int \frac{dy}{1 - y^2}$

Följt av partialbråksuppdelning. Detta trick kan anpassas för en klass av på vissa trigonometriska trationella uttryck men fungerar inte på alla medan tan-halva-gör det. 

Jag tror jag har sovit under delen om partialbråk uppdelning. Varför behövs detta? är inte $\frac{dy}{1-y^2}$ en inre derivata över en över derivata, om man lägger en 2:a? 

Har testat såhär. Vad gör jag fel, förutom partialbråkuppdelning, som på samma sätt vet jag inte när jag ska använda :)?

$$\begin{gathered} \left[9x=u \\ \frac{du}{dx}=9\right] \\ \int \frac{1}{\sin \left(9x\right)}dx = \int \frac{{\displaystyle 1}}{{\displaystyle \sin \left(9x\right)}} \frac{\sin \left(9x\right)}{\sin \left(9x\right)}dx = \int \frac{{\displaystyle \sin \left(9x\right)}}{{\displaystyle {\sin }^2\left(9x\right)}} dx = \\ = \int \frac{{\displaystyle \sin u}}{{\displaystyle {\sin }^2\left(u\right)}} \frac{du}{9} = \frac{{\displaystyle 1}}{{\displaystyle 9}}\int \frac{{\displaystyle \sin u}}{{\displaystyle 1-{\cos }^2\left(u\right)}} du \\ \left[\cos \left(u\right)=y \\ dy=-\sin u du\right] och D{y}^2=2dy \\ \frac{{\displaystyle 1}}{{\displaystyle 9}}·\frac{1}{2}\int \frac{{\displaystyle -dy}}{{\displaystyle 1-y^2}} =\frac{1}{18}\ln \left|1-y^2\right|=\frac{{\displaystyle 1}}{{\displaystyle 18}}\ln \left|1-{\cos }^{2}u\right|=\frac{{\displaystyle 1}}{{\displaystyle 18}}\ln \left|1-{\cos }^2\left(9x\right)\right| \end{gathered}$$

Ett annat brute-force-trick man kan göra är att skriva om sina trigonometriska funktioner på komplex form

$\cos(x) = \frac{e^{ix} + e^{-ix}}{2}$

$\sin(x) = \frac{e^{ix} - e^{-ix}}{2i}$

och substituera för $z = e^{ix}$ men det är något involverat för det mesta. 

 Det har jag försökt och det har slutat illa:

AlvinB skrev:

Pröva att göra en substitution $s=9x$ innan halvvinkelsubstitutuionen så blir du av med nian. :-)

 Uhhh jag kommer fram till 

$\frac{1}{9}\left|\ln x\right|$

Asså I can't control it. 

Varför byter du ut $s$ mot $2\arctan(x)$? $s$ är ju lika med $9x$.

... när exakt måste jag introducera den här dubbelvinkel?

SeriousCephalopod skrev:

Tan-halva-tricket är ett väldigt generellt trick så är rätt värt att lära sig det.

Just 1/sin-integralen är även angripsbar med ett annat trick där man förllänger det rationella uttrycket med en faktor sin(x) vars syfte är att möjliggöra en annan trigonometriskt substitution. 

$\int \frac{dx}{\sin(x)} = \int \frac{\sin (x)dx}{\sin^2 (x)} = \int \frac{\sin(x)}{1 - \cos^2(x)}$

Och därefter med substitutionen $y = \cos x$

$\int \frac{dx}{\sin(x)} = -\int \frac{dy}{1 - y^2}$

Följt av partialbråksuppdelning. Detta trick kan anpassas för en klass av på vissa trigonometriska trationella uttryck men fungerar inte på alla medan tan-halva-gör det. 

 

 ...

....

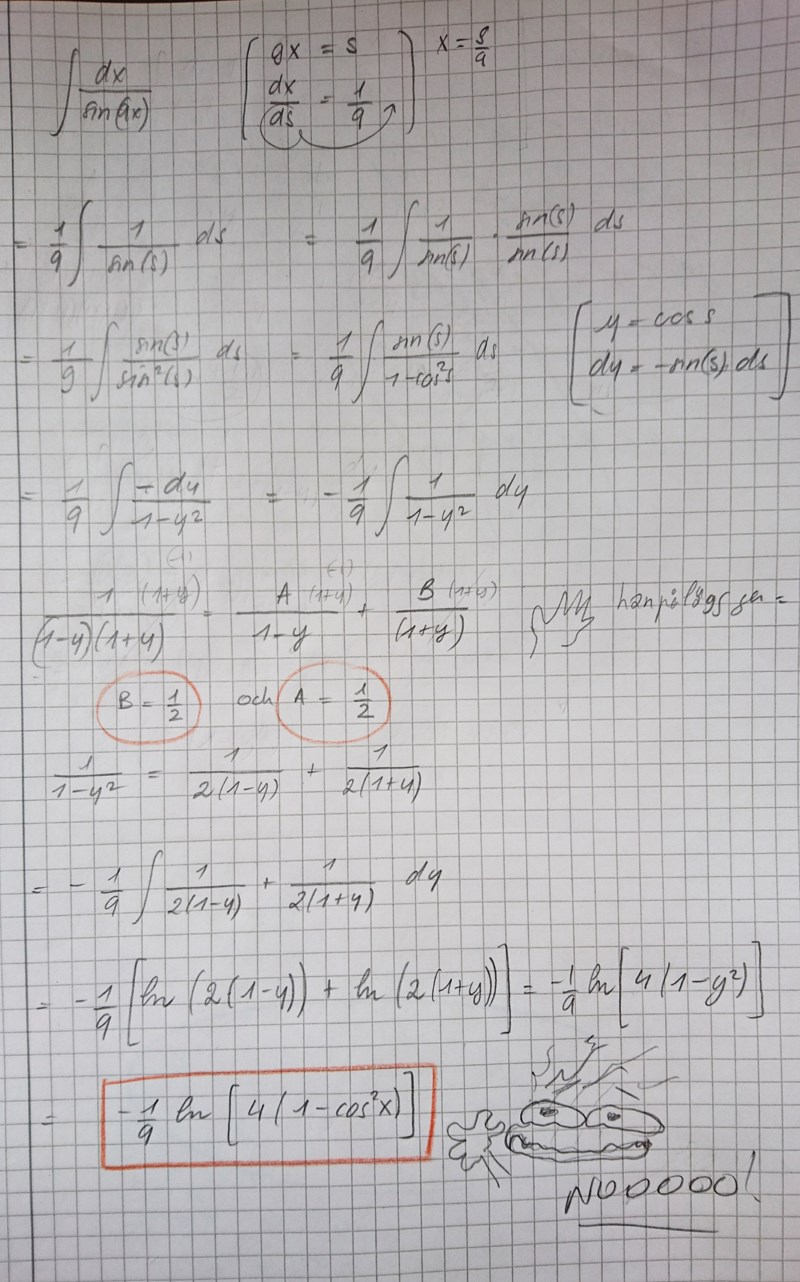
Vilket jobbigt hjärnfrys!

2 dagar redan!

Det klassiska inre-derivata-teckenfelet.

Du har skrivit 

$\int \frac{dx}{1 - y} = \ln(1 - y)$

Men detta är inte rätt för du har inte tagit hänsyn till den inre derivatan $(-y)' = -1$ så rätt vore

$\int \frac{dx}{1 - y} = -\ln(1 - y)$

2 bör även inte läggas inuti logaritmen utan utanför då du annars måste kompensera för dess derivara.

Varför man i slutändan inte tar produkten av de två nämnarna utan kvoten av dem

$\int \frac{dy}{1 - y^2} = \frac{1}{2}\ln|1 + y| - \frac{1}{2}\ln |1 - y| = \frac{1}{2} \ln \left | \frac{1 + y}{1 - y} \right |$

Men ska inte detta 2:a försvinna när jag delar $\ln \left(2\right(1+y\left)\right) - \ln \left(2\right(1-y\left)\right) =\ln \frac{2(1+y)}{2(1-y)}$ ?

Om du för in 2:an inom logaritmfunktionen så måste du ändå introducera en yttre tvåa för att när du deriverar så får du en inre derivata 2 från denna faktor. 

Kontanta faktorer bör vi som regel lägga framför integraltecknet.

Men den värsta är att även:

$-\frac{1}{9}·\frac{1}{2} \ln \left(\frac{1+\cos x}{1-\cos x}\right)$ verkar vara fel svar.

Helt sjukt. Jag borde testa den andra brute force metoden idag....

Usch... efter 3 dagar nästan heltid på detta problem förstådd jag med IntellektuelBläckfisk metod. Jag får dock inte rätt svar med dubbelvinkel metod, så om du orkar Alvin, jag köper den fortfarande.

Dessutom tror jag att det är dag med cosektant? och cosinkant...

Som dr G förskrev (bara att hämta ut receptet på apoteket)

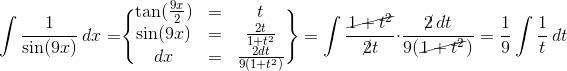
AHA Men det får jag!! Men det blir fel:

$$\int \dfrac{1}{\sin(9 x)} dx \\$$

$$
\left[
\begin{aligned}
9x=u\\
x=\frac{u}{9}\\
\frac{dx}{du}=\frac{1}9
\end{aligned}
\right]$$

$$\int \dfrac{1}{\sin(u)} \dfrac{1}{9} du\\$$

$$
\left[
\begin{aligned}
u=2 \arctan t\\
t= \tan \frac{u}{2}\\
\frac{du}{dt}=\frac{2}{1+t^2}
\end{aligned}
\right]$$

$sin(2arctan(t))= 2 \cdot \frac{t}{\sqrt{1+t^2}} \cdot \frac{1}{\sqrt{1+t^2}}$

$$\dfrac{1}{9} \int \dfrac{\dfrac{2}{1+t^2}}{\dfrac{2t}{1+t^2}} dt\\$$

$$\dfrac{1}{9} \int \dfrac{1}{t} dt\\$$

$$\dfrac{1}{9} ln|t|= \dfrac{1}{9} ln|\tan\dfrac{u}{2}|= ln|\tan\dfrac{9x}{2}|\\$$

EDIT: LaTex:en vill inte komma ut ...

Lite svårt att tyda ditt inlägg utan LaTeX, men om du hänger upp dig på absolutbeloppet eller det faktum att vi måste hålla oss till ett intervall som inte innehåller någon udda multipel av $\pi$ kan du alltså dela upp den naturliga logaritmen enligt

$\displaystyle \frac{1}{9}\ln(\tan(\frac{9x}{2}))=\frac{1}{9}\left(\ln(\sin(\frac{9x}{2}))-\ln(\cos(\frac{9x}{2})) \right)$

Sorry:

Guggle skrev:

Lite svårt att tyda ditt inlägg utan LaTeX, men om du hänger upp dig på absolutbeloppet eller det faktum att vi måste hålla oss till ett intervall som inte innehåller någon udda multipel av $\pi$ kan du alltså dela upp den naturliga logaritmen enligt

$\displaystyle \frac{1}{9}\ln(\tan(\frac{9x}{2}))=\frac{1}{9}\left(\ln(\sin(\frac{9x}{2}))-\ln(\cos(\frac{9x}{2})) \right)$

 Jag fattar literally INTE ett ord av detta.

Alltså jag förstår individuella orden men inte när du gjorde den här mening. Speciellt den här med udda multipel av pi?

dajamanté skrev:

Guggle skrev:

 vi måste hålla oss till ett intervall som inte innehåller någon udda multipel av $\pi$ kan du alltså dela upp den naturliga logaritmen enligt

$\displaystyle \frac{1}{9}\ln(\tan(\frac{9x}{2}))=\frac{1}{9}\left(\ln(\sin(\frac{9x}{2}))-\ln(\cos(\frac{9x}{2})) \right)$

 Jag fattar literally INTE ett ord av detta.

Alltså jag förstår individuella orden men inte när du gjorde den här mening. Speciellt den här med udda multipel av pi?

Substitutionen $t=\tan(x/2)$ kan i princip alltid användas då integranden är bildad av $\sin(x), \cos(x)$ och några konstanter sammanfogade genom addition, multiplikation eller division. Man kan då visa att den nya integranden efter substitutionen alltid blir en rationell funktion.

Det är en sorts SUPERMAN av substitutioner.

Men om det nu är så SUPERBRA, varför använder man den inte ALLTID? För att det ofta leder till SUPERLÅNGA räkningar.

Det finns också en kryptonit (udda multipler av $\pi$).  Om integrationsintervallet innehåller en udda multipel av $\pi$ t.ex. $t=3\pi$ blir ju $\tan(t/2)=\tan(\frac{3\pi}{2})$ vilket är odefinierat (cos(t) blir 0 där).

Slutligen vart tog $1/9$ vägen i ditt sista steg?

En mycket olyckligt olycka har hänt $\dfrac{1}{9}$. 

Nu är det fixat i den ursprungliga dokument (som har 164 kodfel ajajajaj)

Jag måste fundera på detta, jag har aldrig konsidererat det förut..