Högskoleprovet HT-18: lösningar
Denna tråd är tänkt att vara en samlingstråd för lösningarna till matematikdelen från höstens högskoleprov (21 oktober 2018), för den som vill kontrollera sina egna lösningar, träna på tidigare uppgifter, eller är nyfiken.
Regler för tråden:
- Skriv av uppgiften i ord högst upp (proven är olika på olika provställen, därför räcker inte endast nummer)
- En uppgift per inlägg. (Detta medför att man lätt kan permalänka om man har frågor)
- Skriv upp svarsalternativen under frågan
- LaTeX-kod eller formeleditorn är att föredra när det kommer till formler och uträkningar
Om du vill ha fler förklaringar, läs gärna de tråden från VT18.
1. Vilket uttryck betecknar produkten av 14 och summan av 46 och 35?
A:
B:
C:
D:
Vi letar efter produkten av 14 och en summa. Då måste summan, beräknas först och sedan multipliceras med 14. Svaret blir alltså C,
2. Vad är 0,2% av 50?
A: 0,01
B: 0,1
C: 1
D: 10
En användbar räkneregel är att x% av y är samma som y% av x. 0,2% av femtio är alltså samma som femtio procent av 0,2. Femtio procent av 0,2 är samma som hälften av 0,2, och svaret blir då 0,1.
Svar: B, 0,1.
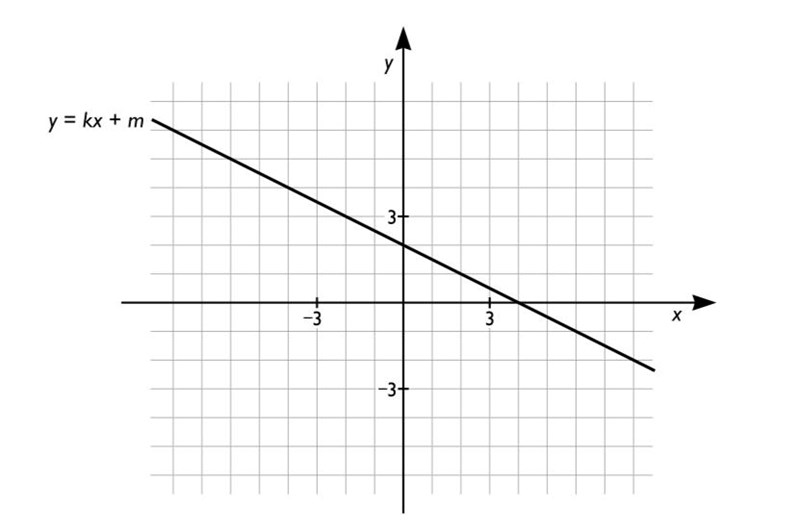
3. Linjen är inritad i ett koordinatsystem. Vilket värde har riktningskoefficienten k?
A:
B:
C: -2
D: 2
En rät linje som avtar (om en tittar från vänster till höger) har ett negativt k-värde. Alltså är alternativ B och D helt uteslutna. Desto brantare lutningen på linjen är, desto högre k-värde. I detta fall är linjen inte särskilt brant. Från punkten där linjen skär y-axeln, (0, 2), till punkten där linjen skär x-axeln, (4, 0), har y-värdet minskat med två steg, medan x-värdet ökat med fyra steg. Lutningen hos en rät linje ges av formeln , där betyder "förändring i". k-värdet är alltså lika med förändringen i y, dividerat med förändringen i y. Alltså är .
Svar: A:
4.
Vilket svarsalternativ är korrekt?
A:
B:
C:
D:
Utveckling av parenteserna ger att:
Subtrahera från båda led, och kvar blir:
Svar: C, .
5. För funktionen f gäller att och . Vilken värdemängd har funktionen?
A:
B:
C:
D:
Värdemängden är mängden av alla värden som funktionen kan spotta ut, givet definitionsmängden. Det minsta värdet är och det största är . Alltså är värdemängden .
Svar: D, .
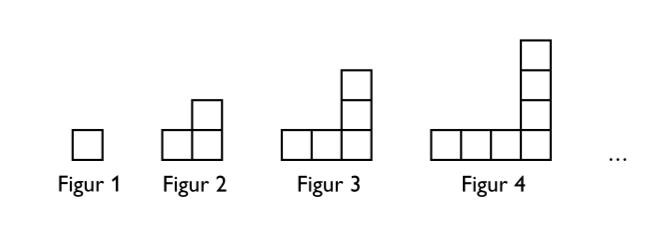
6. Med hjälp av lika stora kvadrater bildas figurer enligt mönstret nedan. Antalet kvadrater i figurerna bildar en aritmetisk talföljd. Hur många kvadrater finns det i figur 150?
A: 298
B: 299
C: 300
D: 301
En aritmetisk talföljd har alltid samma differens mellan termerna, och brukar skrivas på formen , där d är differensen och n är elementnumret. I detta fallet är . Den första figuren har en ruta, den andra figuren har tre rutor, den tredje har fem, osv. Differensen måste alltså vara 2. Då har vi en formel för element nummer n: . Vi sätter in n = 150 i formeln och får:
Svar: B, 299.
7.
Vad är x?
A: 0
B:
C:
D:
Flytta över alla konstanta termer till högerledet, och kvar blir:
Det går att dividera båda led med sexton niondelar, men det går snabbare att förlänga bråket i högerledet med tre, och få:
Som kan förenklas till ekvationen .
Svar: C, .
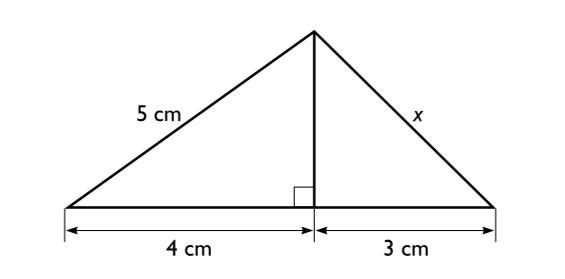
8. Vad är sidlängden x?
A: 3 cm
B:
C: 3,5 cm
D: cm
Höjden i triangeln kan fås med Pythagoras sats, . Samma höjd kan sedan användas för att räkna ut sidan x med samma formel: .
Svar: B, .
a och b är två på varandra följande heltal. Hur stor är sannolikheten att är jämnt delbart med 2?
A: 0
B: 0,25
C: 0,5
D: 1
Tal som är jämnt delbara med två är jämna. Två på varandra följande heltal utgörs alltid av ett jämnt och ett udda tal, eftersom vartannat heltal är udda. Ett jämnt tal plus ett udda tal blir alltid udda, och därmed kan summan av två på varandra följande heltal aldrig vara jämn, och därmed aldrig jämnt delbar med två.
Svar: A, 0.
En rektangel med längden 2 dm och bredden 5 cm utgör basytan av ett rätblock som har höjden 3 m. Vilken volym har rätblocket?
A: 30
B: 30
C: 300
D: 300
Volymen av ett rätblock är lika med $$V=\text{längd}\cdot\text{bredd}\cdot\text{höjd}$$. Längden och bredden ges av rektangeln, 2 dm respektive 5 cm. En av enheterna måste omvandlas till den andra. Valet spelar egentligen ingen roll, men för enkelhetens skull väljs en av de två enheter som förekommer i facit, kubikdecimeter. 5 cm = 0,5 dm. Höjden är 3 meter, vilket motsvarar 30 decimeter. Då kan volymen beräknas (eftersom alla mått är givna i decimeter blir enheten kubikdecimeter):
Svar: B, .
11. Vilket svarsalternativ ger alla lösningar till olikheten ?
A:
B:
C:
D:
Subtrahera 2x från båda led:
Addera åtta till båda led:
Svar: A, .
12. Vilket svarsalternativ är ett heltal?
A:
B:
C:
D:
Summan av A och B kommer aldrig att bli heltal. Decimalerna tar inte ut varandra. Då kvarstår C och D som möjliga alternativ. C är lika med . Eftersom detta tal inte kan skrivas som något tal x dividerat med tre, , kommer trean inte att göra talet till ett heltal.
Då kvarstår endast D, vilket är det korrekta alternativet. För den som vill beräkna D är den potenslag som säger att mycket användbar. , och roten ur nio är lika med tre, ett heltal.
13.
I:
II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
För x större än ett gäller det att desto högre potens, desto snabbare växer funktionen.
Svar: A, I är större än II.
14.
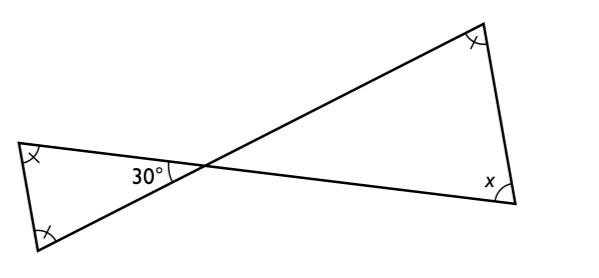
Kvantitet I: x
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Eftersom den vänstra triangeln är likbent, kan dessa vinklar benämnda med ett streck beräknas till 75 grader. Vinklarna i skärningen mellan de två linjerna är lika stora, båda är 30 grader. Eftersom den övre vinkeln i den högra triangeln är lika stor som de vänstra vinklarna i den vänstra triangeln, 75 grader, kan x beräknas med hjälp av att vinkelsumman i en triangel är 180 grader:
Svar: B, II är större än I.
15.
Kvantitet I:
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Det är svårt att förenkla denna uppgift. Det är lättast att bara räkna med hjälp av minsta gemensamma nämnare:
Svar: A, I är större än II.
16.
Kvantitet I: x
Kvantitet II: y
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Vi löser ekvationerna:
Svar: B, II är större än I.
17. I rektangeln ABCD finns ett skuggat område.
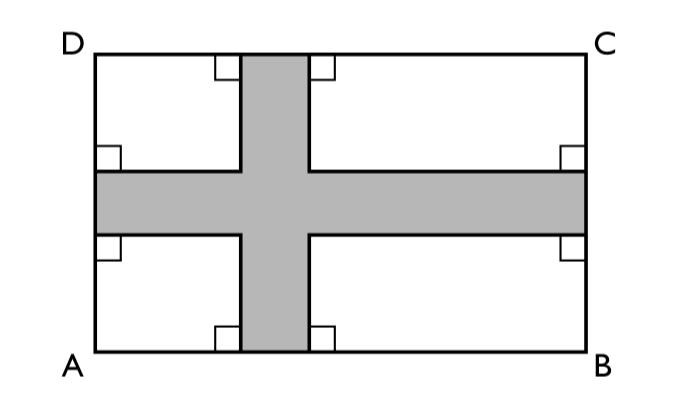
Kvantitet I: Omkretsen av rektangeln ABCD
Kvantitet II: Omkretsen av det skuggade området
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Om två hörn i en fyrhörning är räta, måste även de andra två hörnen vara räta. Det innebär att rektanglarnas ena långsida plus ena kortsida är precis lika långa som den andra långsidan plus den andra kortsidan. De blå sidorna nedan är alltså lika långa som de oranga. De gröna sidorna är gemensamma för både I och II.

Därför är omkretsen av korset och omkretsen av rektangeln lika stora.
Svar: C, I är lika med II.
x, y, z och w är fyra positiva tal sådana att .
Medianen av x, y och z är 7.
Medianen av y, z och w är 13.
Kvantitet I: Medianen av y och z
Kvantitet II: 11
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Medianen är det tal som står i mitten i en serie storleksordnade tal. Eftersom medianen av x, y och z är 7, måste y vara lika med sju. Medianen av y, z och w (13) ger att z är lika med tretton. Vid medianberäkning av en serie tal med jämnt antal element, som medianen av y och z, tas medelvärdet av de två mittersta talen. Medianen av y och z är alltså .
, vilket innebär att svaret är B, II är större än I.
19.
Kvantitet I:
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Kvantitet I kan förenklas med hjälp av att , och blir då lika med . Eftersom täljarna nu är identiska återstår frågan om 2 eller roten ur fem är större. Vi kan dra till minnes att , och då kan vi konstatera att .
Svar: A, I är större än II.
20.
Kvantitet I: 21% av 2482
Kvantitet II: 42% av 1241
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Notera att , och att . I kvantitet II tar vi alltså en dubbelt så stor procent, men av en hälften så stor mängd. Det medför att den del som faktiskt tas är lika stor i I som i II.
Svar: C, I är lika med II.
21. För funktionen f gäller att och .
Kvantitet I:
Kvantitet II: 0
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
, och . Kvantitet I blir då lika med . Det är givet att a är ett positivt tal, och produkten blir alltså negativ.
Svar: B, II är större än I.
22. David är 8 år äldre än Frida. Edvin är 11 år.
Kvantitet I: Summan av Edvins ålder och Fridas ålder
Kvantitet II: Davids ålder
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Subtrahera Fridas ålder från båda kvantiteter. Då är I lika med Edvins ålder (11 år) och II lika med "Davids ålder fast utan Fridas år", dvs. 8 år.
Svar: A, I är större än II.
23. På ett bort ligger två blyertspennor, en gul och en brun. Hur många centimeter längre än den gula pennan än den bruna?
(1) Pennornas sammanlagda längd är 21 cm.
(2) Den gula pennan är 15 cm lång. Den bruna pennan är 0,4 gånger så lång som den gula pennan.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Den gula pennan kan vara 18, 19, 20 cm (eller något annat mått där den gula pennan är längre än den bruna). Det ger flera olika värden, och (1) är alltså inte tillräcklig.
(2): Vi får veta hur lång den gula pennan är, samt ett förhållande för den bruna pennan. Vi kan beräkna hur lång den bruna pennan är, och därmed få reda på skillnaden i längd. (2) är alltså tillräcklig.
Svar: B, i (2) men ej i (1).
24. Vilket värde har x?
(1)
(2)
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Detta påstående medför att flera olika värden på x och y är möjliga. Det är alltså inte tillräckligt för att besvara frågan.
(2): Vi har att ett värde på y, och en ekvation med x och y. Det innebär att vi endast har en okänd variabel, och vi kan lösa ekvationen.
Svar: B, i (2) men ej i (1).
25. En affär säljer strömbrytare styckvis. Om man köper färre än tio så gäller ett visst pris, och om man köper tio eller fler så får man 8 % rabatt på det totala priset. Hur mycket kostar det att köpa 16 strömbrytare vid ett och samma tillfälle?
(1) Det kostar 479,20 kr att köpa 8 strömbrytare.
(2) Om man köper 10 strömbrytare så får man 47,92 kr i rabatt.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Vi kan beräkna priset av en strömbrytare med denna information. Multiplikation av styckpriset med 16, tillsammans med att det är givet att vi får åtta procent rabatt, ger totalpriset för 16 strömbrytare. (1) är alltså tillräckligt.
(2): Vi vet att rabatten är 47,92 kronor, och att detta motsvarar åtta procent av totalpriset. Vi kan då beräkna det totala priset och få ut ett styckpris. Det kan användas för att beräkna totalpriset, och (2) är alltså tillräckligt med information.
Svar: D, i (1) och (2) var för sig
26. I ett stall finns det tre boxar bredvid varandra med en häst i vardera boxen: en hingst, ett sto och ett föl. Hästarna har varsin färg: brun, svart och vit. I mitten står stoet.Vilken färg har fölet?
(1) Hingsten är svart och står bredvid den bruna hästen.
(2) Stoet, som står till höger om hingsten, är inte vitt.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Eftersom stoet står i mitten, kan hästarnas uppställning antingen vara F | S | H eller H | S | F. Oavsett om hingsten står till höger eller till vänster om stoet, måste stoet vara den bruna hästen som står bredvid hingsten. Hingsten är svart och stoet är brunt. Då måste fölet vara vitt.
(2): Vi vet nu att uppställningen är H | S | F, men vi vet ingenting om färgerna. Stoet är inte vitt, men kan vara både svart och brunt. Fölet och hingsten kan ha alla tre färger. (2) ger inte tillräckligt med information.
Svar: A, i (1) men ej i (2).
27. Eva köper en lott i ett lotteri. Hur stor är sannolikheten att lotten är en vinstlott?
(1) Andelen nitlotter är 80 procent.
(2) Det finns 250 lotter i lotteriet.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): En lott är antingen en nitlott eller en vinstlott. Om vi vet andelen nitlotter, vet vi också andelen vinstlotter, och därmed sannolikheten att lotten är en vinstlott.
(2): Att det finns 250 lotter i lotteriet säger ingenting om uppsättningen av lotter. Det kan vara en vinstlott och 249 nitlotter eller 249 vinstlotter och en nitlott, eller någon annan uppsättning. (2) ger inte tillräckligt med information.
Svar: A, i (1) men ej i (2).
28. Utanför en skolbyggnad finns det en cykelparkering med ett antal cyklar. Hur många cyklar finns det på parkeringen?
(1) 19 av cyklarna har pakethållare och 13 av cyklarna har fotbroms.
(2) 11 cyklar har varken pakethållare eller fotbroms.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
Antalet cyklar är lika med .
(1): Detta påstående ger ingen information varken om hur många cyklar som inte har någondera, eller om hur många cyklar som har båda. Det räcker alltså inte för att definitivt avgöra hur många cyklar som finns.
(2): Detta påstående ger information om $$A_{ej fotbroms, ej pakethållare}, men inte om någon av de andra mängderna. Det räcker alltså inte för att definitivt avgöra hur många cyklar som finns.
Tillsammans: Vi vet fortfarande inte hur många cyklar det finns som har både pakethållare och fotbroms. Det kan vara alltifrån noll cyklar som har båda till att alla cyklar som har pakethållare har fotbroms. Inte ens tillsammans ger de båda påståendena tillräckligt med information.
Svar: E, ej genom de båda påståendena.
Anställda i utlandsägda företag: (29 - 31)
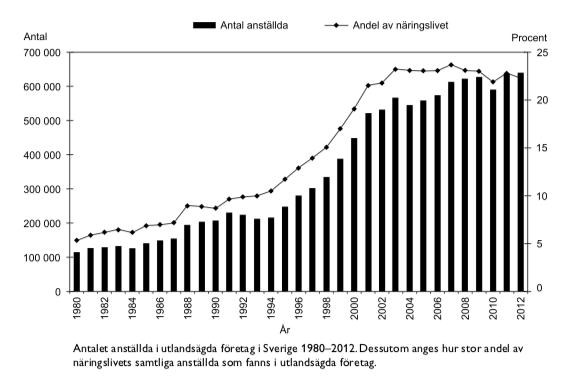
29. För hur många av de redovisade åren gäller att antalet anställda i utlandsägda företag minskade jämfört med närmast föregående år?
A: 5
B: 6
C: 7
D: 9
Räkna antalet dippar:
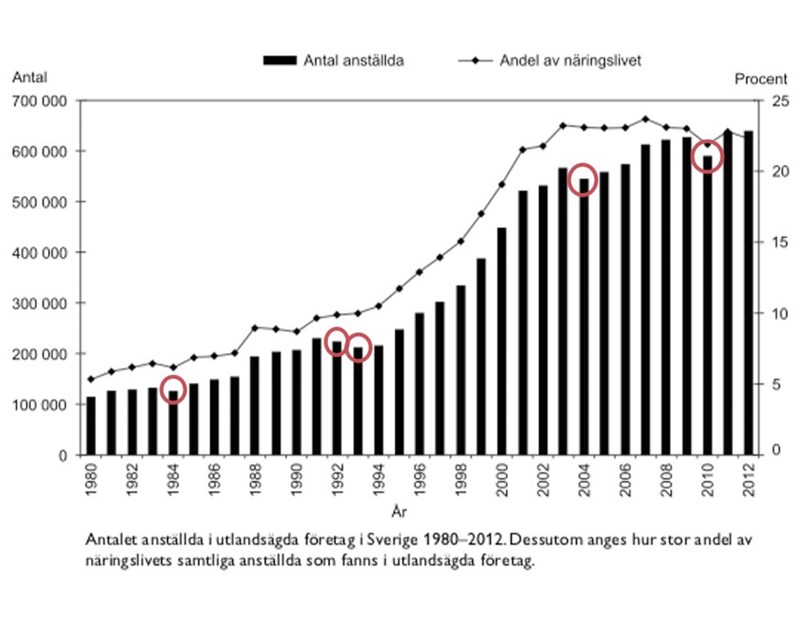
Svar: A, 5.
30. Vilket år var antalet anställda i utlandsägda företag 400 000–600 000 och utgjorde 15–20 procent av näringslivets samtliga anställda?
A: 1998
B: 1999
C: 2000
D: 2001
Eftersom åren är nära varandra är det värt att markera de olika kraven i diagrammet:
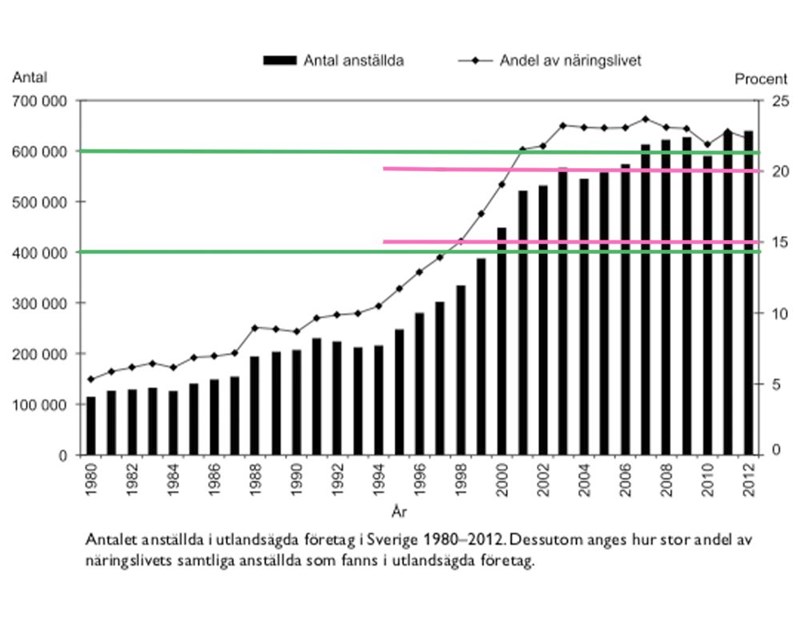
Tre år faller inom intervallet för procentandel, 1998, 1999 och 2000, men endast en av dessa uppfyller kravet på antal anställda. Kvar är endast alternativ C, 2000.
Svar: C, 2000.
31. Studera hur många anställda i utlandsägda företag det fanns 1993 samt hur stor andel av näringslivets samtliga anställda de utgjorde.Hur många anställda fanns det totalt inom näringslivet
i Sverige detta år?
A: 5
B: 6
C: 7
D: 9
Markeringar av året 1993 ger:
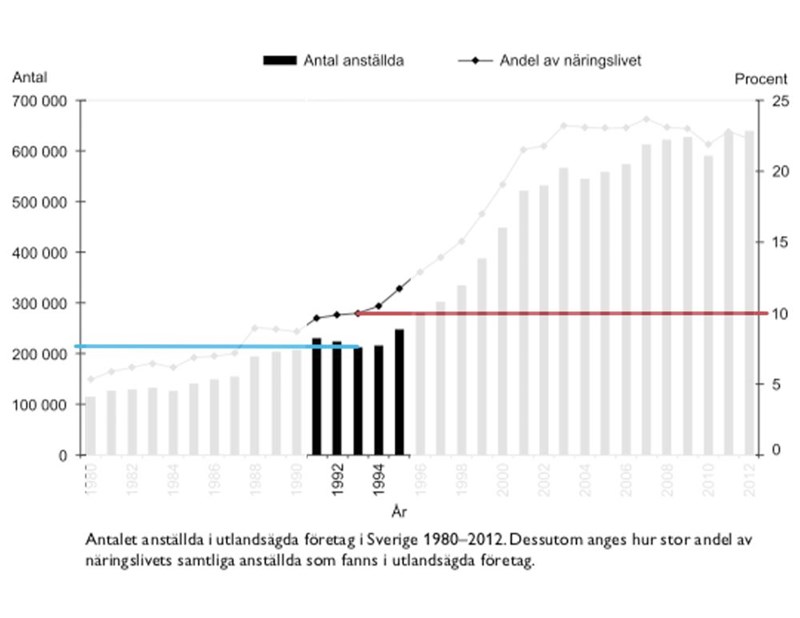
Antalet anställda var strax över 200 000, och de utgjorde nästan exakt tio procent av det totala antalet anställda. . Alternativ C, 2 050 000, passar nästan perfekt.
Svar: C, 2 050 000.
Berggrund och jordarter på Öland: (32 - 34)
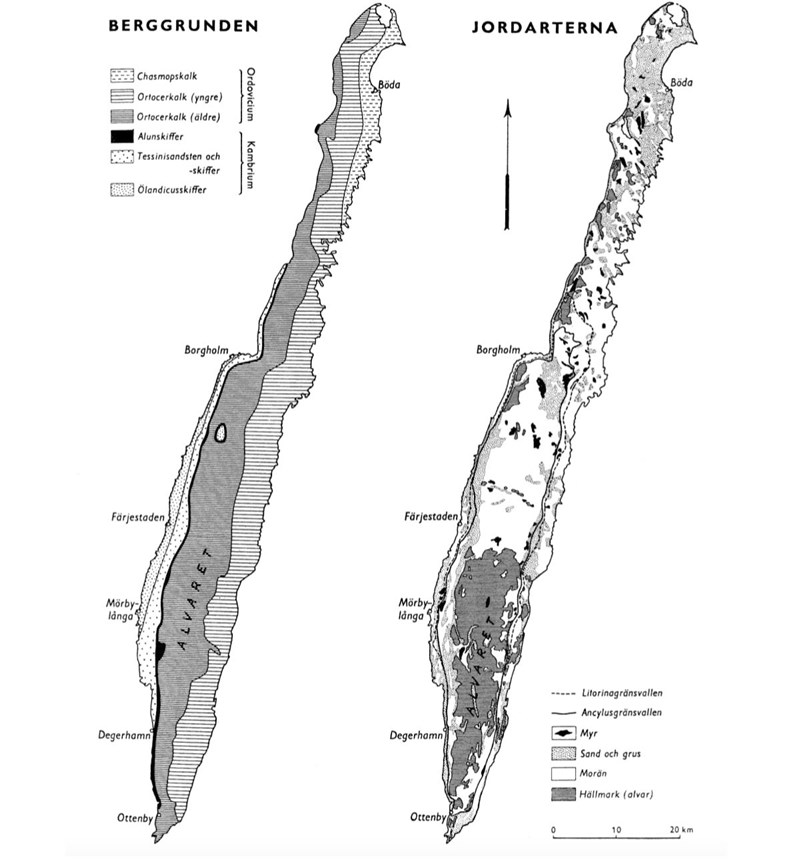
32. Om man delar Öland i höjd med Borgholm i en nordlig och en sydlig del, vilken berggrund är då vanligast i den nordliga respektive sydliga delen?
A: Ortocerkalk (yngre) respektive Ortocerkalk (äldre)
B: Ortocerkalk (yngre) respektive Chasmopskalk
C: Ortocerkalk (äldre) respektive Ortocerkalk (yngre)
D: Chasmopskalk respektive Ortocerkalk (äldre)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Dra en linje i diagrammet:
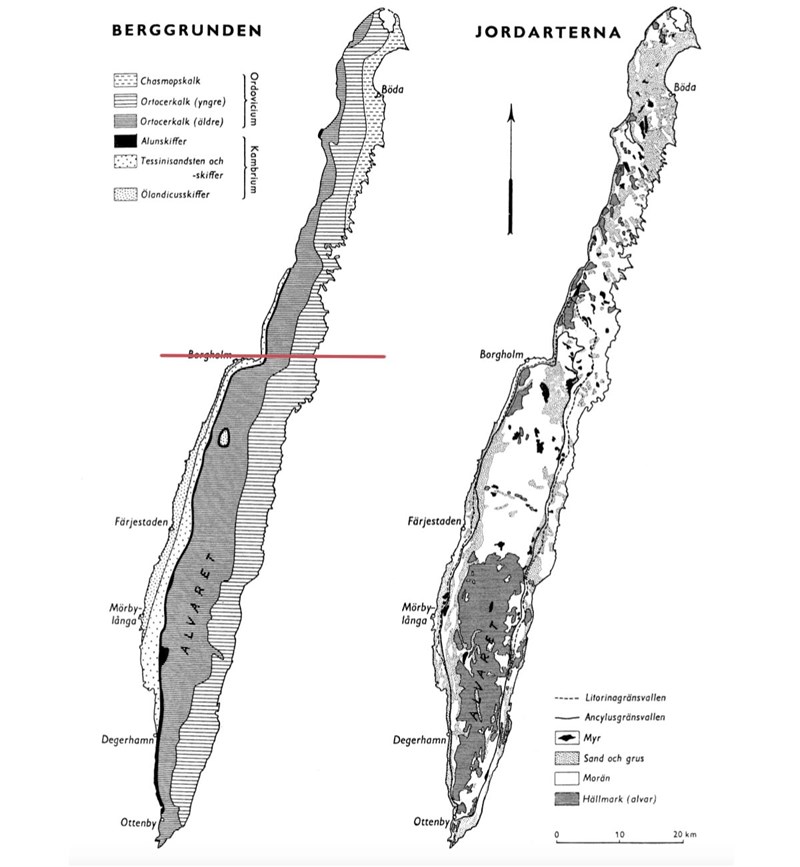
Och vi kan konstatera att Ortocerkalk (äldre) är klart vanligast i den södra delen. Då kvarstår alternativ A och alternativ D. I den norra delen finns en del Chasmopskalk, men det är inte den vanligaste berggrunden. Då kvarstår endast alternativ A.
Svar: A, Ortocerkalk (yngre) respektive Ortocerkalk (äldre)
33. Vilka två jordarter förekommer närmast Ölands östkust rakt öster om Mörbylånga?
A: Myr samt morän
B: Myr samt hällmark
C: Sand och grus samt morän
D: Sand och grus samt hällmark
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Rita en linje vid Mörbylånga i diagrammet:
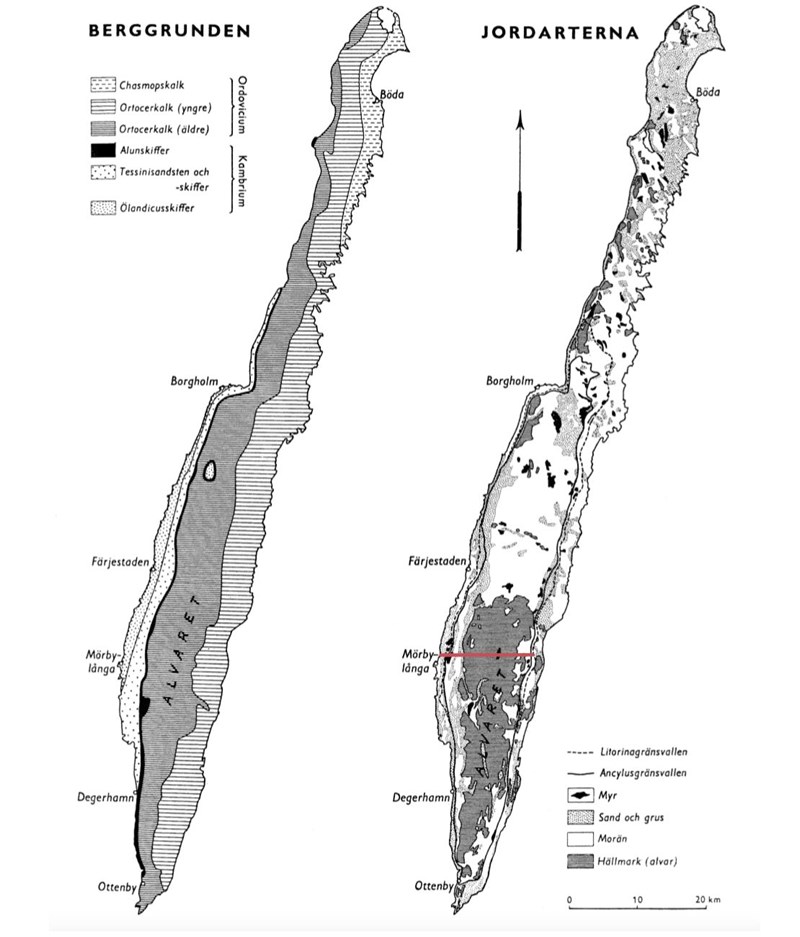
Närmast finns Hällmark. De alternativ som kvarstår är då B och D. Det finns ingen myr i närheten och därmed är svaret D.
Svar: D, Sand och grus samt hällmark
34. För vilken ort gäller att den ligger i ett område med ölandicusskiffer och att närmaste förekomst av chasmopskalk finns cirka 70 km fågel- vägen från orten?
A: Borgholm
B: Degerhamn
C: Färjestaden
D: Mörbylånga
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Mät upp en linje som är 7 km lång, och undersök alternativen. Borgholm, alternativ A, ligger alldeles för nära chasmopskalksområdet, och Degerhamn, alternativ D, ligger alldeles för långt bort. Då har vi två alternativ kvar, och vi kan rita in den linje vi mätt upp i diagrammet:
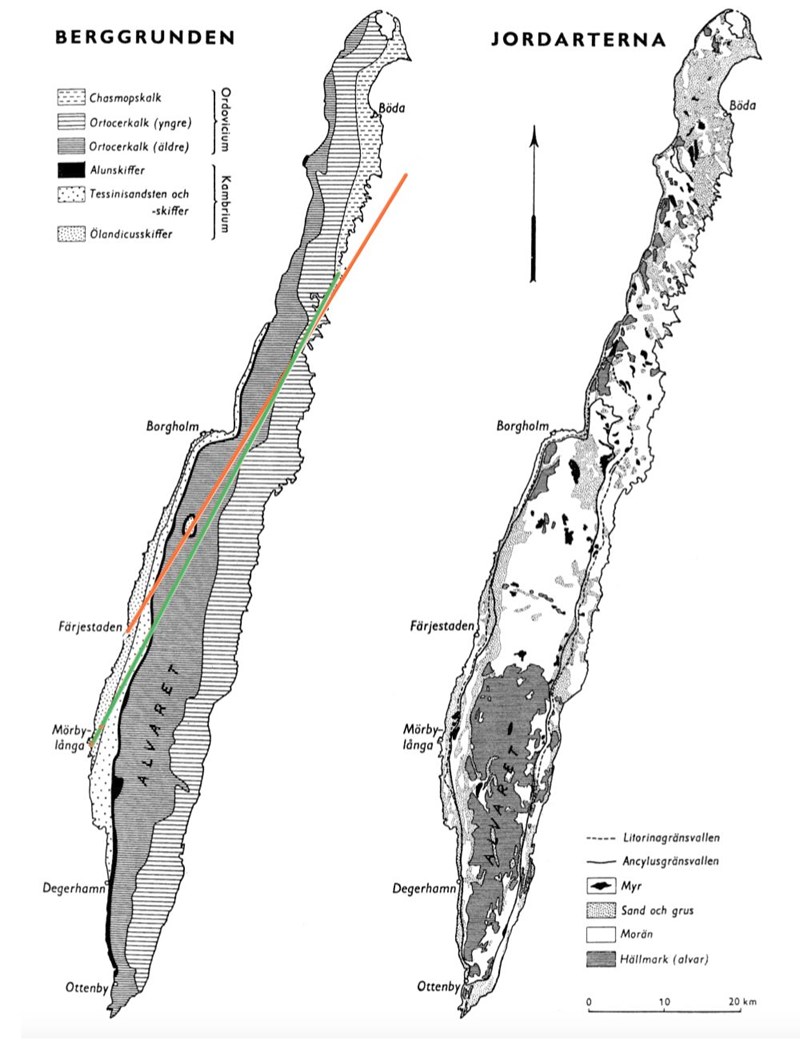
Den orangea linjen, från Färjestaden, är för lång, medan den gröna linjen, från Mörbylånga, passar perfekt.
Svar: D, Mörbylånga.
Svenskars internetanvändning:
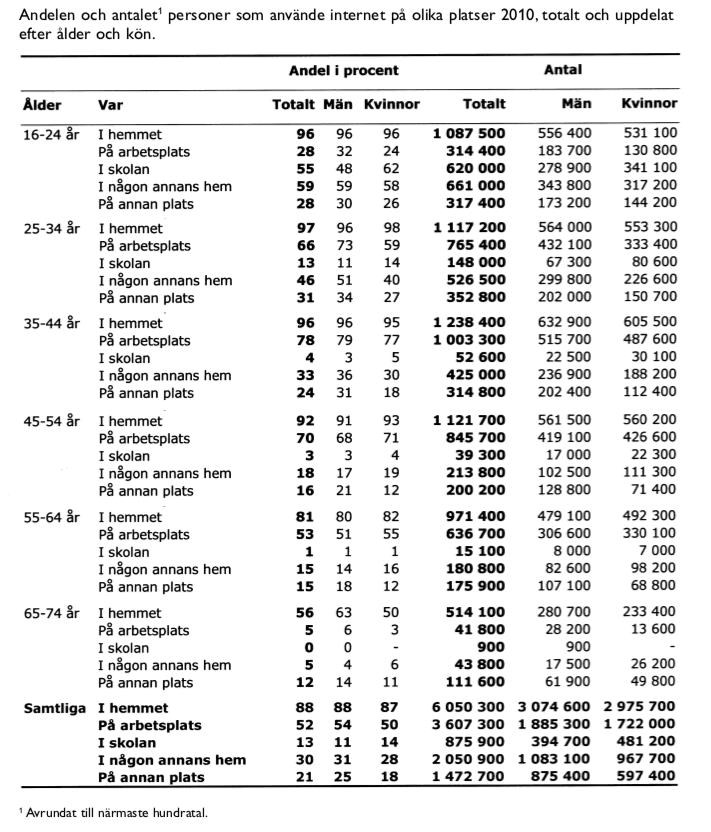
I vilken kategori noterades den största skillnaden i antal mellan män och kvinnor?
A: 16–24-åringar som använde internet i skolan
B: 25–34-åringar som använde internet på arbetsplatsen
C: 25–34-åringar som använde internet på annan plats
D: 35–44-åringar som använde internet på annan plats
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Markera de relevanta siffrorna i diagrammet:
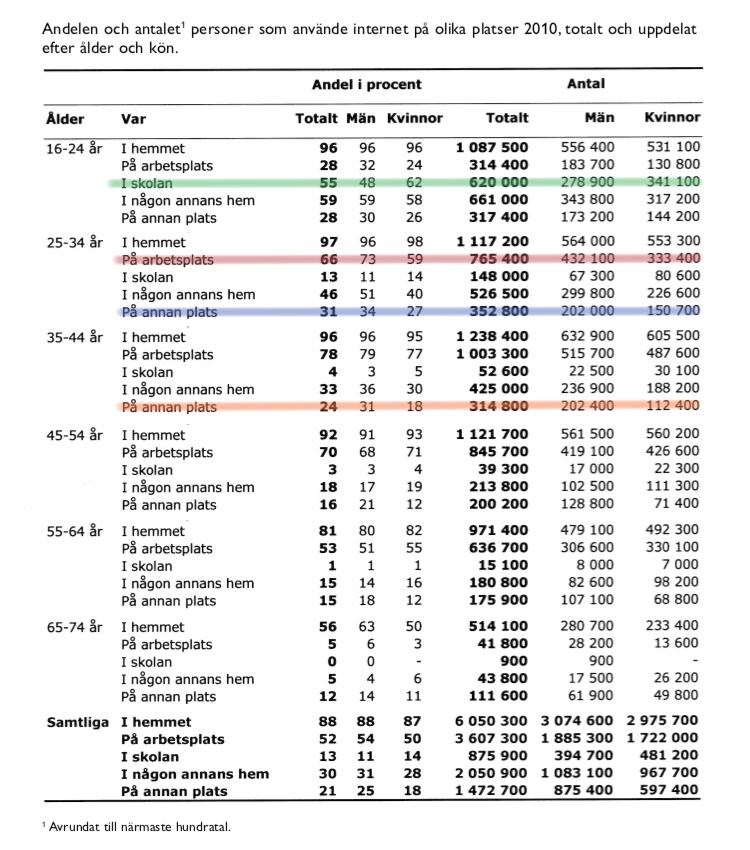
Alternativ A: Skillnaden är , alltså 42 000. Ingen särskild skillnad.
Alternativ B: Skillnaden är , skillnaden är 99 000 personer.
Alternativ C och D: Givet att skillnaden inte är större än 100 000 personer, är alternativ B svaret. En snabb titt i diagrammet visar att skillnaderna är cirka 50 000 respektive 90 000.
Svar: B, B: 25–34-åringar som använde internet på arbetsplatsen
I totalgruppen var de som använde internet hemma ungefär tre gånger så många som de som använde internet i någon annans hem. Vilken åldersgrupp var mest lik totalgruppen i detta avseende?
A: 16–24-åringar
B: 25–34-åringar
C: 35–44-åringar
D: 45–54-åringar
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
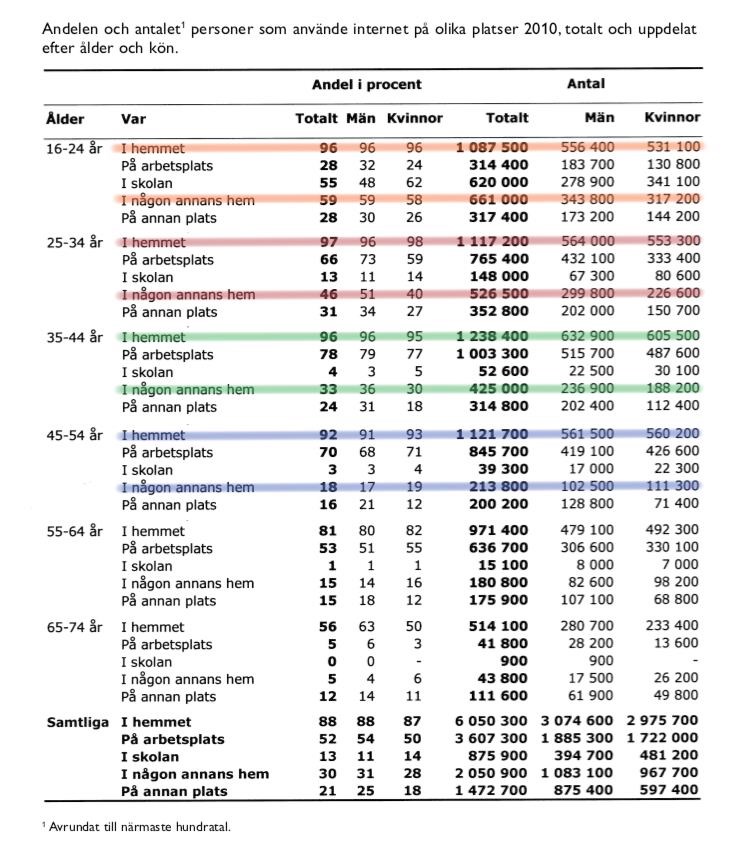
Börja med att utesluta allt som är långt ifrån en tredjedel, vilket är alternativ A (över hälften) och D (mindre än en fjärdedel). Även alternativ B kan uteslutas då alternativet är i närheten av hälften. Kontroll av alternativ C ger att C är ganska precis en tredjedel.
Svar: C, 35 - 44-åringar
Hur stor andel av alla som använde internet på arbetsplatsen var under 45 år?
A: 78 procent
B: 58 procent
C: 48 procent
D: 28 procent
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
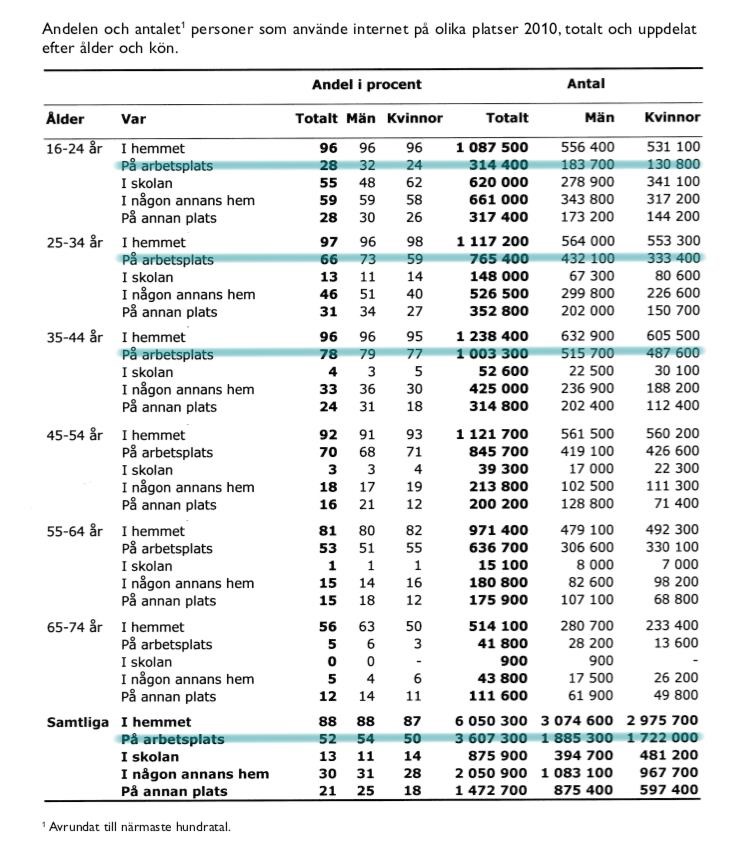
Den totala siffran är drygt 3 600 000. Summan av gruppen "under 45 år" är . Andelen blir då . Svaret ska alltså vara lite över femtio procent. B, 58 procent passar alltså utmärkt.
Svar: B, 58 procent.
Folkbibliotekens utlåning: (38 - 40)
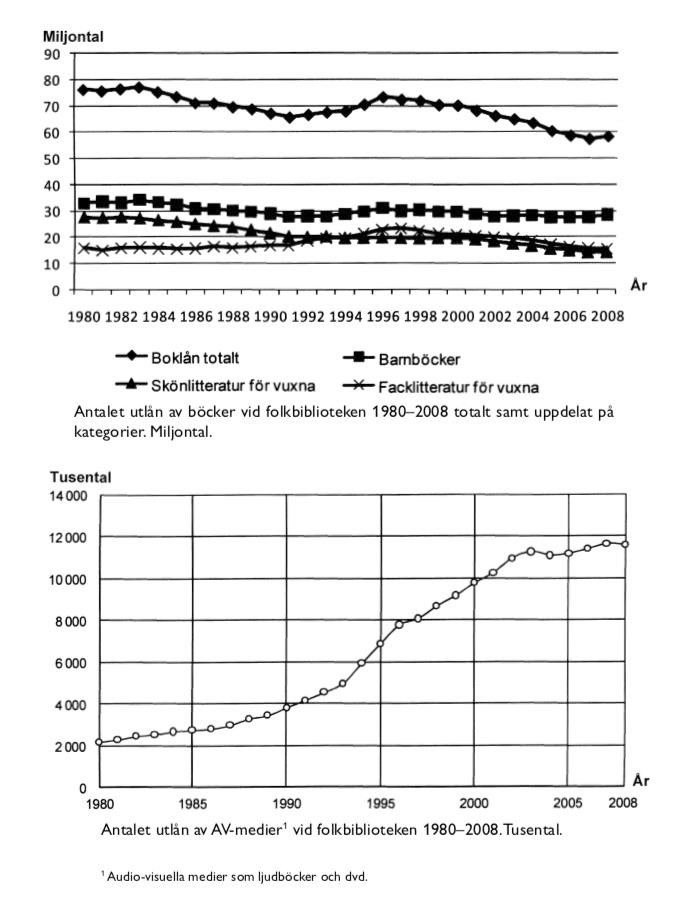
38. Vilket av följande år avses?
Antalet boklån totalt var mindre än 70 miljoner och antalet utlån av AV-medier ökade med en miljon jämfört med året innan.
A: 1991
B: 1993
C: 1994
D: 1996
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Markera linjen för 70 miljoner utlånade böcker. Då kan alternativ D, 1996, uteslutas, eftersom antalet lån var högre än 70 miljoner.
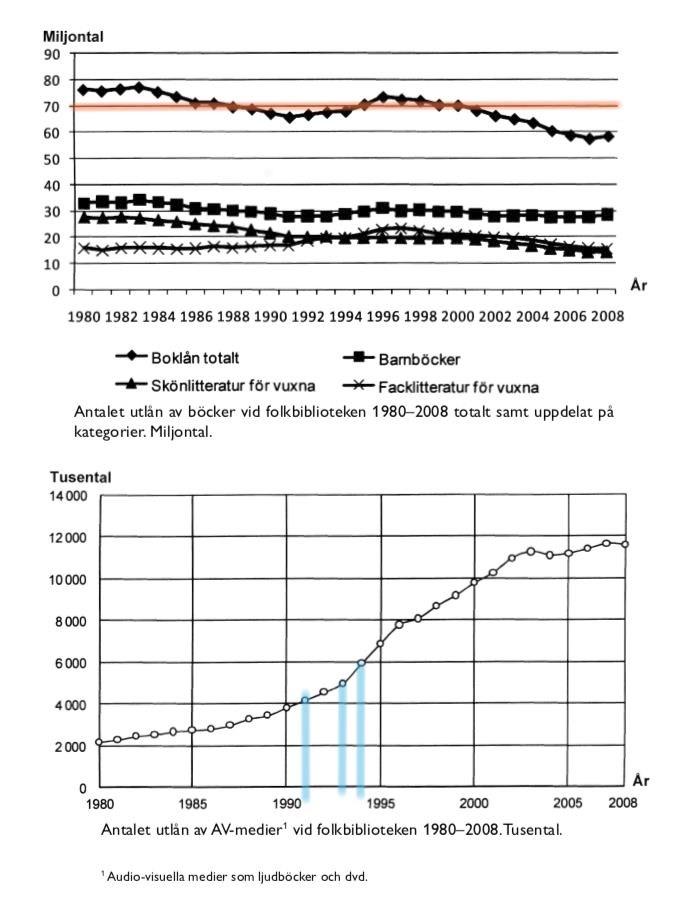
En ökning med en miljon AV-lån är hälften av ett snäpp på y-axeln i grafen. Endast ett år uppfyller detta, vilket är alternativ C, 1994.
Svar: C, 1994.
39. I folkbibliotekens bokbestånd fanns 2008 cirka 40 miljoner böcker. Hur många gånger i genomsnitt lånades en bok ut detta år?
A: 0,70 gånger
B: 1,10 gånger
C: 1,45 gånger
D: 1,85 gånger
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Undersök det totala antalet lån:
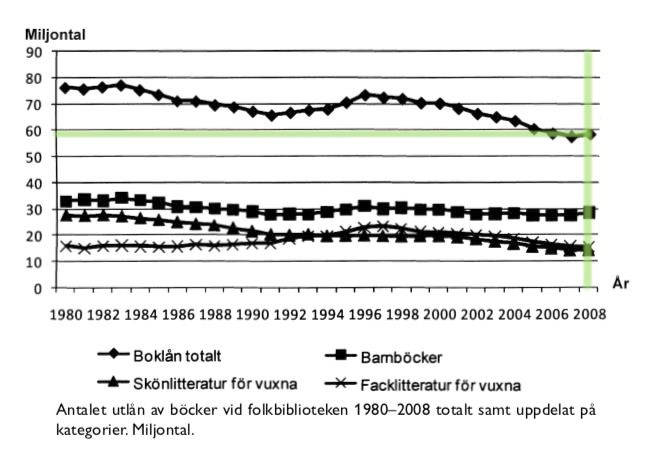
Antalet lån var strax under 60 miljoner. Genomsnittet av antalet lån per bok blir då . Eftersom antalet lån var lite under 60 miljoner, letar vi efter ett svar som är aningen under 1,5. Alternativ C passar då mycket bra.
Svar: C, 1,45 gånger.
40. Hur många av boklånen år 2000 var utlån av barnböcker?
A: Fem av tio
B: Fyra av tio
C: Tre av tio
D: Två av tio
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
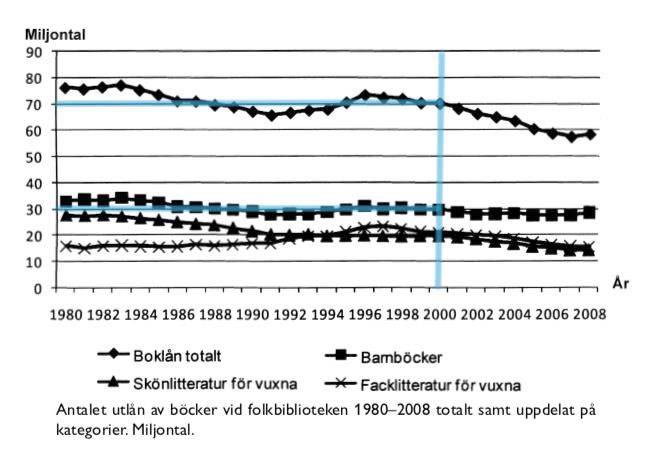
Antalet barnbokslån var 30 miljoner, och det totala antalet var 70 miljoner. Det ger andelen , vilket är strax under hälften. Det alternativ som passar bäst är fyra av tio.
Svar: B, fyra av tio.
Del två av de kvantitativa proven.
1. Vilket av svarsalternativen motsvarar uttrycket
A:
B:
C:
D:
Använd den potenslag som säger att . Då blir svaret .
Svar: B,
2. Vilket svarsalternativ motsvarar en punkt som inte är markerad i koordinatsystemet nedan?
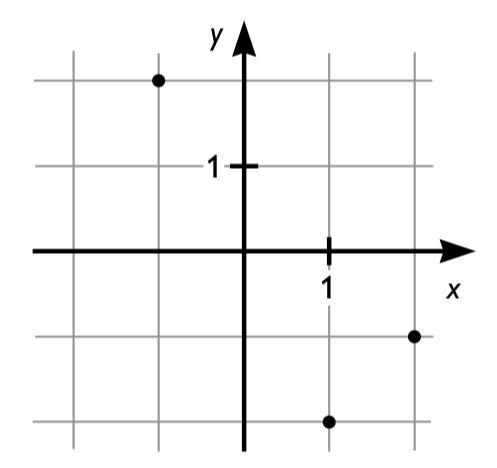
A: (-2, 1)
B: (-1, 2)
C: (1, -2)
D: (2, -1)
Studera x-axeln. Det finns en punkt markerad då x = -1, 1 och 2. Det enda svar som inte har någon punkt markerad är det svar där x = -2, vilket är A.
Svar: A, (-2, 1).
3.
Vilket av svarsalternativen är större än 1?
A:
B:
C:
D:
Alternativ B och D kan direkt uteslutas, då nämnaren är större än täljaren. Dessutom kan alternativ C uteslutas av samma anledning, täljare och nämnare subtraheras med samma tal, men b är mindre än c. Alltså blir nämnaren större än täljaren och kvoten blir mindre än ett.
Svar: A, .
4. och är parallella linjer. Hur stor är vinkeln x?
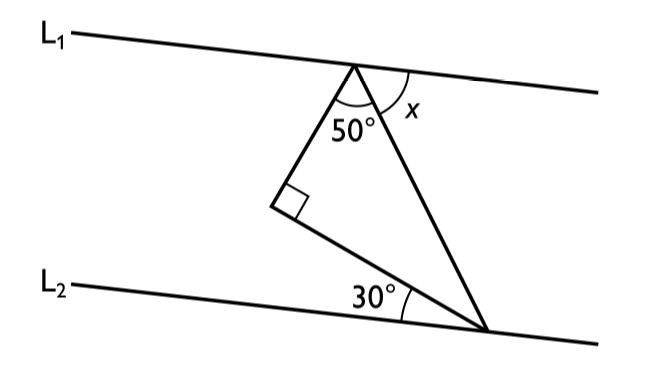
A:
B:
C:
D:
Sätt ut några hjälpvinklar i figuren först:
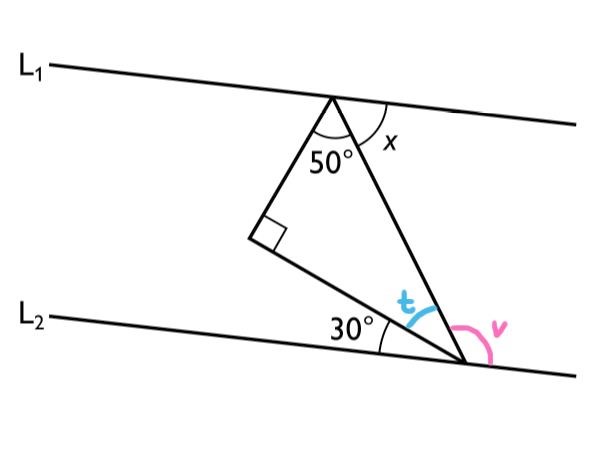 t kan beräknas till 40 grader, eftersom vinkelsumman i en triangel alltid är 180 grader. Det gäller även att eftersom de tillsammans bildar vinkeln hos en rät linje. Därmed kan v beräknas till 110 grader. Dessutom måste , eftersom linjerna och är parallella. Då kan x konstateras vara 70 grader.
t kan beräknas till 40 grader, eftersom vinkelsumman i en triangel alltid är 180 grader. Det gäller även att eftersom de tillsammans bildar vinkeln hos en rät linje. Därmed kan v beräknas till 110 grader. Dessutom måste , eftersom linjerna och är parallella. Då kan x konstateras vara 70 grader.
Svar: C: .
5. Vad är ?
A:
B:
C:
D: 6
Det gäller att , och därmed att . Genom att faktorisera täljare och nämnare fås att . Förenkling ger då svaret .
Svar: A, .
6. De sex talen 5, 15, 17, 23, x och y har medelvärdet 11. Vad är medelvärdet av talen x och y?
A: 1
B: 3
C: 6
D: 9
Medelvärdet för de sex talen är . Multiplikation med sex i båda led ger att . Medelvärdet av x och y är då .
Svar: B, 3.
7. Vilket av svarsalternativen motsvarar förhållandet 6:7?
A: 36:49
B: 67:76
C: 120:140
D: 330:390
Alternativ A är kvadraterna av de individuella termerna i förhållandet. Det ger inte samma förhållande. A kan därför uteslutas.
Alternativ B innehåller en udda siffra som ersättare för 6. Alla jämna heltal förblir jämna när de multipliceras med ett annat heltal, jämnt eller udda. Eftersom 67 är ett udda tal kan den faktor som termerna multiplicerats med inte vara ett heltal, men eftersom det tal 7 ersatts med är ett heltal kan B inte vara samma förhållande.
Alternativ C kan direkt förenklas till 12:14, vilket är samma sak som . Detta är vårt svar.
För säkerhets skull kan alternativ D kontrolleras. Detta alternativ kan förenklas till 33:39, vilka båda är primtal och alltså inte kan motsvara 6:7.
Vilket av svarsalternativen motsvarar uttrycket?
A:
B:
C:
D: 0
Förenkling ger att .
Svar: C, .
9. Summan av tre på varandra följande heltal är 96. Vad är produkten av det minsta och det största talet?
A: 992
B: 1023
C: 1056
D: 1096
Talen kan skrivas som . Deras summa är . De tre talen är alltså 31, 32 och 33. Produkten av det minsta och det största talet är .
Svar: B, 1023.
10. där m är en konstant.
Vad är ?
A: 1
B: a
C: m
D: 3
Sätt in (a + 1) respektive a i formeln. Det ger att .
Svar: D, 3.
11. Vad är ?
A:
B:
C: 40
D:
Skriv bråket som två separata bråk:
Förenkling ger då .
Svar: D,
12. Tre linjer och en cirkel avgränsar den skuggade ytan i figuren. Vilken area har den skuggade ytan?
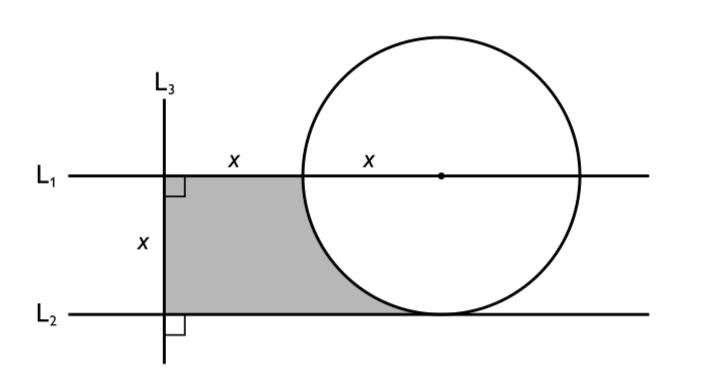
A:
B:
C:
D:
Rita en linje från mitten av cirkeln, så att en rektangel bildas:
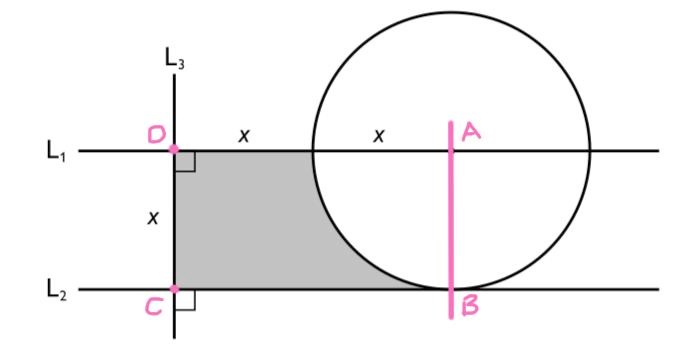
Det skuggade områdets area är lika med ABCDs area minus den fjärdedel av cirkeln som finns med. ABCD har sidorna x respektive 2x, och har alltså arean . Eftersom cirkeln har radien x, har den arean . En fjärdedel av cirkeln har då arean , och det skuggade området har arean .
Svar: D, .
13.
Kvantitet I: x
Kvantitet II: y
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Det gäller att , vilket innebär att de två ekvationerna kan förenklas till och . Eftersom det enda som skiljer vänsterleden från varandra är x respektive y, och den undre ekvationen är större än den övre, är x < y.
Svar: B, II är större än I.
14. Kvantitet I: Medelvärdet av fem positiva och fem negativa heltal
Kvantitet II: 0
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Beroende på vilka de ingående talen är, blir medelvärdet större än, mindre än eller lika med noll. Om de negativa talen alla är -500, och de positiva talen alla är +2, kommer medelvärdet bli negativt. Om de positiva talen är lika med 500 och de negativa lika med -2 blir medelvärdet negativt. Det går alltså inte att avgöra något med denna information.
Svar: D, informationen är otillräcklig.
15. Kvantitet I: Omkretsen av en cirkel med diametern 1 cm
Kvantitet II: Omkretsen av en liksidig triangel med sidan 1 cm
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Omkretsen av en cirkel ges av , där d är diametern. Omkretsen av en triangel fås genom att addera längden av dess sidor. Det ger att:
I = cm
II = 3 cm.
Pi är ungefär 3,14, vilket är större än 3.
Svar: A, I är större än II.
16. x och y är två på varandra följande heltal sådana att .
Kvantitet I: 2x
Kvantitet II: Summan av x och y
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Börja med att gissa ett förhållande, säg att I > II. Vi ställer upp det:
, vilket inte är sant. Vi vet att x < y. Då vet vi att II > I, men den som känner sig osäker kan gärna testa detta påstående:
, vilket är korrekt enligt informationen från uppgiften.
Svar: B, II är större än I.
17. Kvantitet I: 0,00541 km
Kvantitet II: mm
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
En kilometer är tusen meter. Kvantitet I är alltså samma som 5,41 m. En meter är också tusen millimeter, vilket innebär att kvantitet II är lika med 5,41 m.
Svar: C, I är lika med II.
18. x och y är positiva heltal.
Kvantitet I: 20
Kvantitet II: x
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
.
Ytterst få tal uppfyller detta förhållande. De tal som uppfyller detta är , , där k är ett positivt heltal. Om k = 1, blir x = 20, och I = II, men om k är än ett större blir II större än I. Vi har två olika resultat, alltså räcker inte den givna informationen.
Svar: D, informationen är otillräcklig.
19.
A=() B = (y_{2}$$)
Punkterna A och B ligger på linjen .
Kvantitet I:
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
En linje med ett negativt k-värde lutar nedåt när en ser från höger till vänster. Det innebär att när x-värdet ökar, minskar y-värdet. Eftersom måste då .
Svar: A, I är större än II.
20.
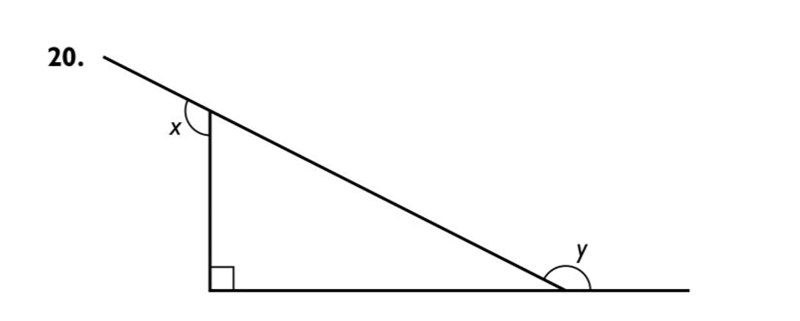
Kvantitet I:
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Kalla komplementvinkeln till x för a, och komplementvinkeln till y för b. Vinkelsumman i en triangel är alltid , och vinklarna i den rätvinkliga triangeln kan summeras som . Eftersom linjerna är räta gäller det att och . Substitution av a och b med de nya uttrycken ger ekvationen .
Svar: C, I är lika med II.
21.
Kvantitet I:
Kvantitet II:
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Omvandling till minsta gemensamma nämnare ger att kvantitet I är lika med tre åttondelar, och likaså kvantitet II.
Svar: C, I är lika med II.
22. Ett badkar rymmer 200 liter.
Kvantitet I: Tiden det tar att fylla badkaret till 54 om man fyller på med den konstanta hastigheten 15 liter per minut
Kvantitet II: Tiden det tar att fylla badkaret till 23 om man fyller på med den konstanta hastigheten 10 liter per minut
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräcklig
Volymen är lika med tiden multiplicerat med påfyllnadshastigheten. Det ger:
I: .
II: .
Svar: B, II är större än I.
23. Tre askar – en blå, en vit och en röd – innehåller olika saker. En ask innehåller gem, en innehåller häftstift och en innehåller nålar. Vilken färg har asken som innehåller gem?
(1) Häftstiften är i den blå eller den röda asken.
(2) Nålarna är i den röda eller den vita asken.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Om häftstiften är i den blå eller röda asken, utan några andra begränsningar, finns det (minst) två möjliga alternativ som skulle kunna fungera. (1) är alltså inte tillräckligt.
(2): Om nålarna är i den vita eller röda asken, utan några andra begränsningar, finns det (minst) två möjliga alternativ som skulle kunna fungera. (2) är alltså inte tillräckligt.
Tillsammans: Vi undersöker om det kan finnas flera godtagbara alternativ. Häftstiften kan vara i den blå eller röda asken, och nålarna i den röda eller vita asken.
Nål - Röd
Häft - Blå
Gem - Vit
Nål - Vit
Häft - Röd
Gem - Blå
Det finns alltså mer än ett godtagbart alternativ. Inte ens tillsammans räcker alltså informationen.
Svar: E, ej genom de båda påståendena.
24. På ett fartyg fanns det 2500 personer under en resa. Var och en av personerna på fartyget var antingen passagerare eller sjöman. Hur stor andel av sjömännen var sjösjuka under resan?
(1) Sju av sjömännen var sjösjuka under resan.
(2) Det fanns nio gånger så många passagerare som sjömän på fartyget.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Sju sjösjuka sjömän säger inget om andelen. Dessa sju kan ha utgjort hela besättningen eller bara en liten del av den. (1) är alltså inte tillräckligt.
(2): Förhållandet mellan besättning och passagerare är bra att ha, men säger inget om hur många sjösjuka sjömän som fanns ombord. (2) är alltså inte tillräckligt.
Tillsammans: Vi vet hur många sjömännen var, eftersom denna siffra kan beräknas från (2), samt hur många som var sjösjuka. Andelen sjösjuka sjömän kan då beräknas.
Svar: C, i (1) tillsammans med (2).
25.
Vilket värde har x?
(1)
(2)
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Ekvationen har två lösningar, ±3, men eftersom x är strikt mindre än noll är endast en av dessa lösningar godkända. Värdet på x är alltså känt med hjälp av informationen i (1).
(2): Beroende på värde på b kommer värdet av x att variera. Det finns många godkända värden på b, som ger helt olika värden på x. Informationen i (2) räcker alltså inte.
Svar: A, i (1) men ej i (2).
26. De tre siffrorna 5, 6 och 7 står skrivna på rad på ett papper. Vilket tresiffrigt tal bildar siffrorna?
(1) Siffran 7 står först.
(2) Talet är större än 758.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): Möjliga alternativ är då 765 och 756, två olika alternativ. (1) är inte tillräckligt.
(2): Om talet är större än 758 är endast ett alternativ möjligt, vilket är 765. (2) är alltså tillräckligt.
Svar: B, i (2) men ej i (1).
27. I en låda finns det 72 enfärgade bollar, röda och blå. Var och en av bollarna är antingen stor eller liten. Hur stor andel av bollarna är stora?
(1) 1/3 av de blå bollarna är stora.
(2) 1/2 av de röda bollarna är små.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
Varken (1) eller (2) för sig ger tillräckligt med information, eftersom de båda berättar om förhållandet mellan stora och små bollar för blå respektive röd, men tillsammans kanske? Vi vet att en tredjedel av de blå bollarna och hälften av de röda bollarna är stora. Däremot vet vi ingenting om färguppsättningen. Eftersom andelen stora och små bollar inte är lika för de olika färgerna kan vi inte göra något mer med denna information. Om det är väldigt många blå bollar blir andelen stora bollar lägre, och om det är fler röda bollar blir andelen högre. Vilket det är förblir okänt med uppgiftens information.
Svar: E, ej genom de båda påståendena.
28. Arean av en rätvinklig triangel är 50 . Hur stora är triangelns vinklar?
(1) Triangeln är likbent.
(2) Minst en av triangelns vinklar är 45°.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena
(1): En rätvinklig, likbent triangel har två olika vinkelstorlekar, 90 och 45 grader. Eftersom vinkelsumman i en triangel inte får överstiga 180 grader, måste triangelns vinklar vara 90, 45 och 45 grader. Denna information är tillräcklig.
(2): Om minst en av vinklarna är 45 grader i en rätvinklig triangel, kan det tredje hörnet beräknas med hjälp av att vinkelsumman i en triangel är 180 grader, och då kan alla tre vinklar bestämmas.
Svar: D, i (1) och (2) var för sig.
Nationalparker och naturreservat: (29 - 31)
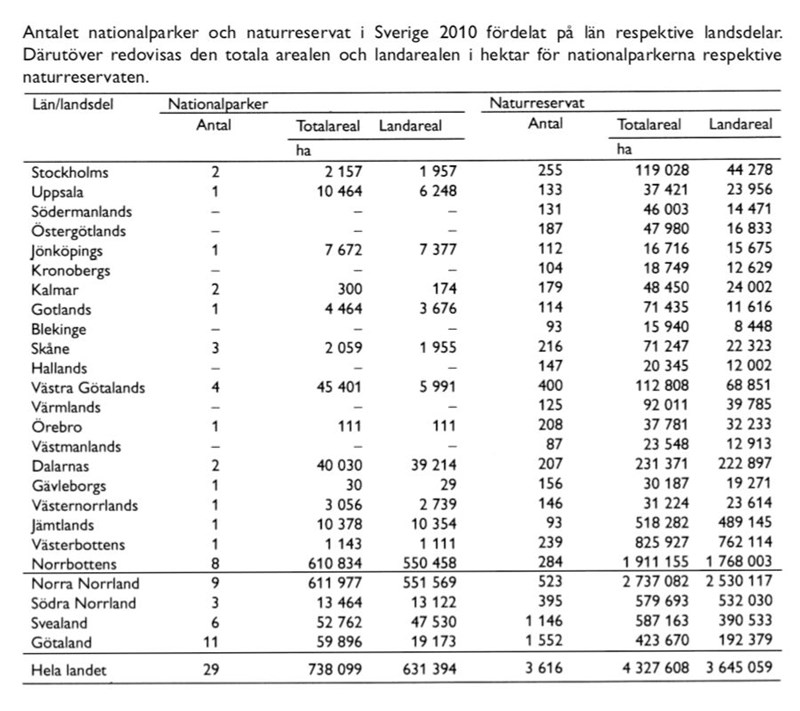
29. Hur många av de 21 länen hade både nationalpark och naturreservat?
A: 3/5
B: 2/3
C: 3/4
D: 4/5
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Räkna antalet län som inte har nationalparker, markerade med streck i diagrammet:
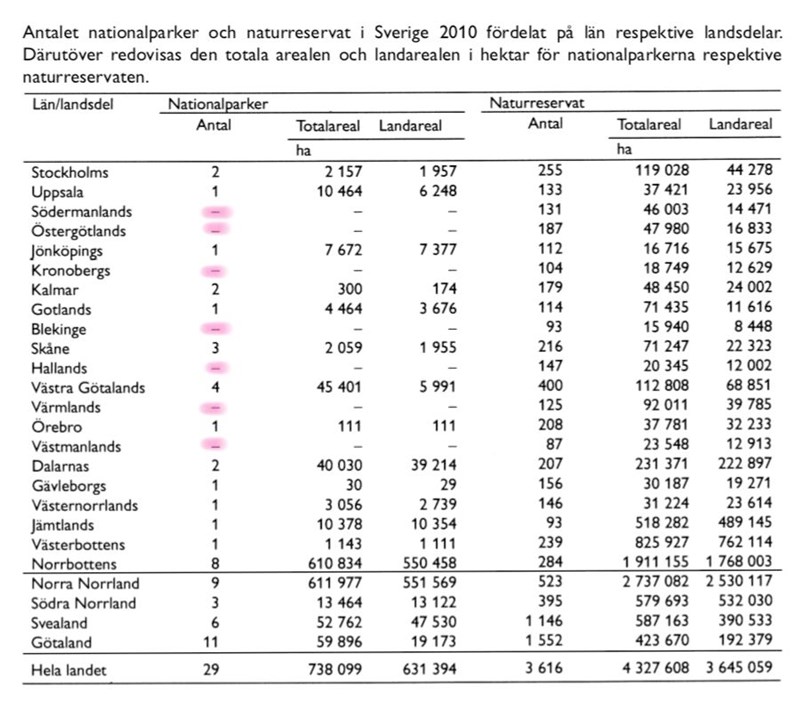
De är sju stycken, alltså har fjorton län både nationalpark och naturreservat. Det motsvarar två tredjedelar av länen.
Svar: B, 2/3.
30. Hur stor andel av totalarealen i Gotlands läns naturreservat utgjordes av landareal?
A: 15 procent
B: 25 procent
C: 60 procent
D: 80 procent
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Undersök den relevanta radens information:
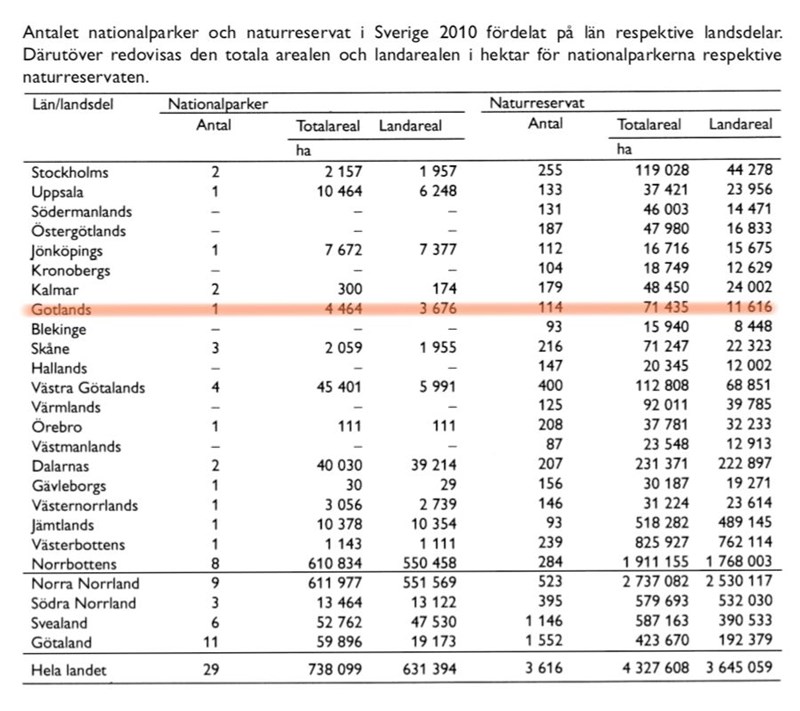
Landarealen är 11 616 hektar, jämfört med totalarealen 71 435 hektar. En ungefärlig beräkning, .
Svar: A, 15 procent.
31. Vilken landsdel hade minst landareal per nationalpark?
A: Norra Norrland
B: Södra Norrland
C: Svealand
D: Götaland
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Markera de relevanta uppgifterna i diagrammet:
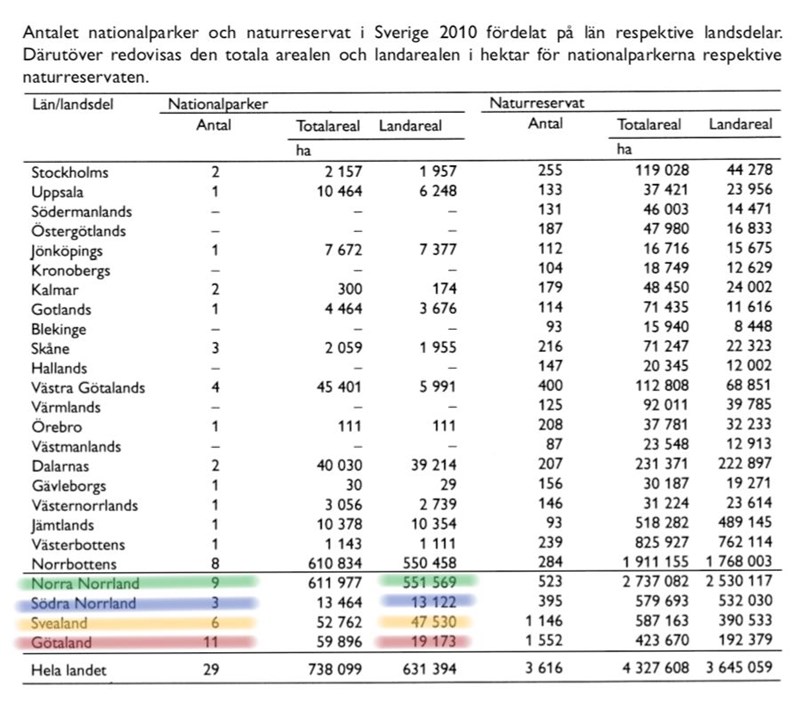
Norra Norrland har väldigt mycket mark, till nio nationalparker. Det är inte minst landareal, och A kan uteslutas. Södra norrland har ungefär 6000 hektar landareal per park, Svealand har drygt 8000 hektar (och kan då uteslutas). Götaland har knappt 2000 hektar. Tre av fyra alternativ måste beräknas i denna uppgift, men de flesta beräkningar går fort, om en rimlig avrundning görs.
Svar: D, Götaland.
Konsumtion av frukt och grönsaker: (32 - 34)
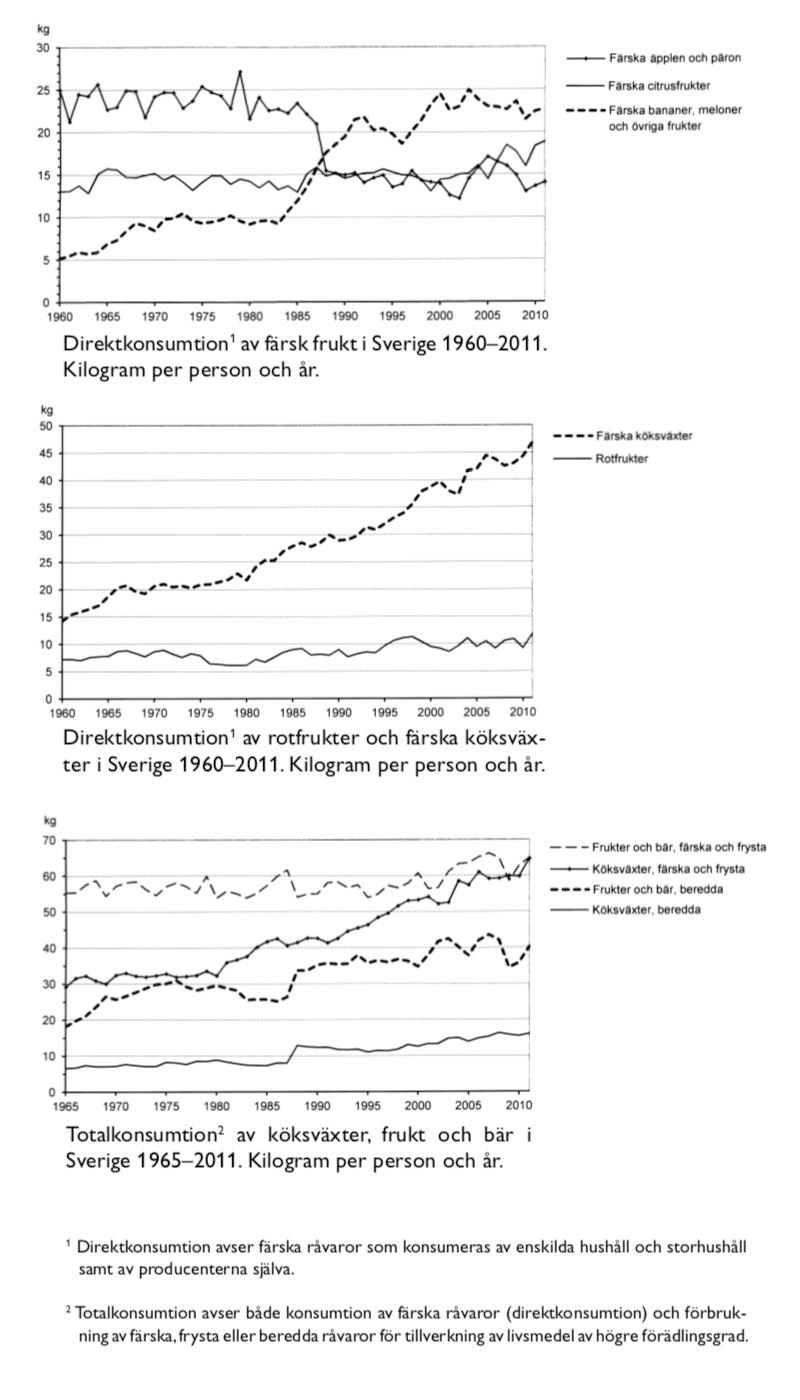
32. Vilket av följande år var den sammanlagda direktkonsumtionen av färsk frukt som störst, räknat per person?
A: 1970
B: 1980
C: 1990
D: 2000
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Markera de relevanta åren i diagrammet:
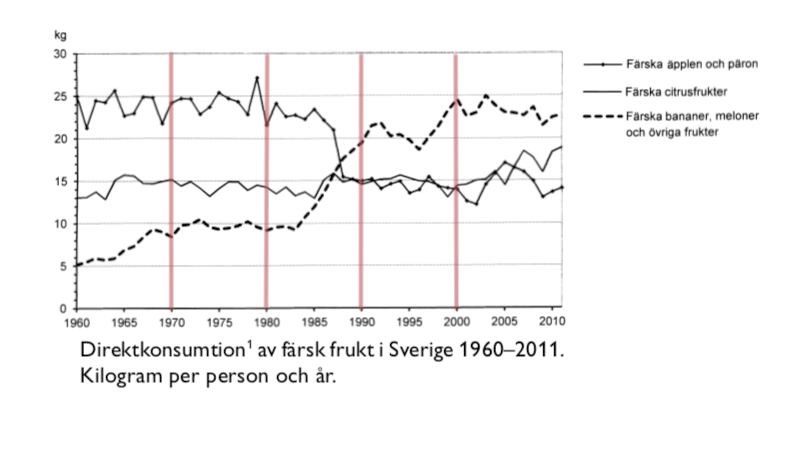
Totalsumman av varje år måste sedan beräknas.
1970: kg
1980: Nästan exakt samma siffror som 1970, men med en märkbar dipp i äppel- och päronkonsumtionen.
1990: kg
2000: kg
Svar: D, 2000.
33. Hur stor var direktkonsumtionen per person av rotfrukter samman lagt för den femårsperiod då konsumtionen var som störst?
A: 45 kg
B: 55 kg
C: 65 kg
D: 75 kg
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Den period som är störst är något klurig att hitta, men utgörs av åren 1995/1996 - 2000. Under denna tid var rotfruktskonsumtionen per år strax över tio kilo per person. Den totala mängden blir då lite över 55 kg per person under perioden, vilket svarar perfekt mot alternativ B, 55 kg.
Svar: B, 55 kg.
34. Hur stor var konsumtionen per person av färska bananer, meloner och övriga frukter 1985 jämfört med konsumtionen per person av färska äpplen och päron samma år?
A: Hälften så stor
B: Två tredjedelar så stor
C: Lika stor
D: Dubbelt så stor
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Markera det relevanta året i diagrammet:
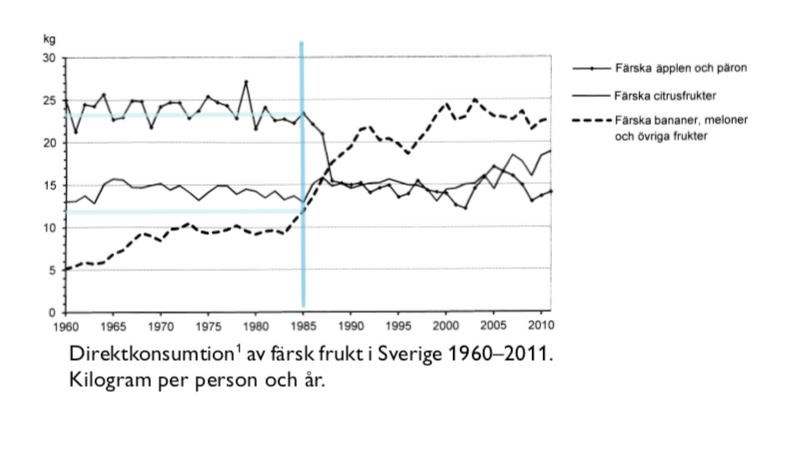
Melon-/banan-/övrigtkonsumtionen var tolv kilogram per person, medan päron-/äppelkonsumtionen var ungefär 23 kilogram. Konsumtionen av melonfrukter var alltså hälften så stor som äppelkonsumtionen.
Svar: A, hälften så stor.
Meritvärde och behörighet bland niondeklassare i Sverige: (35 - 37)
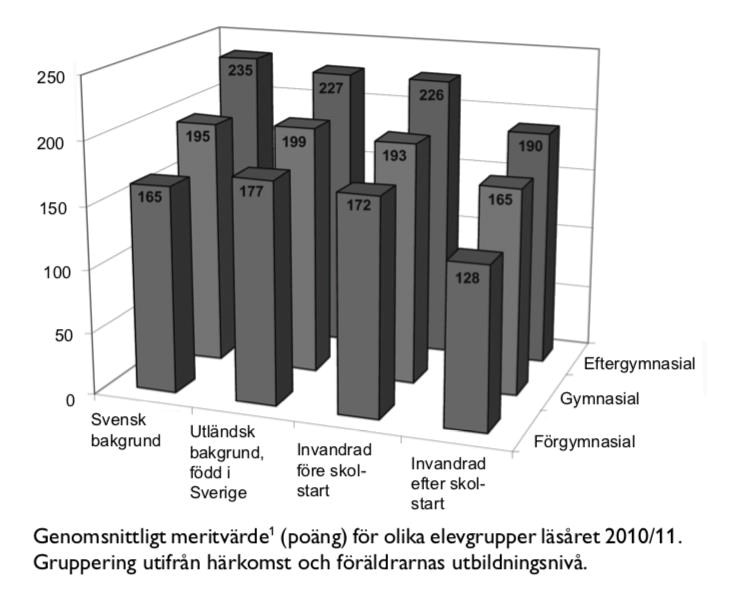
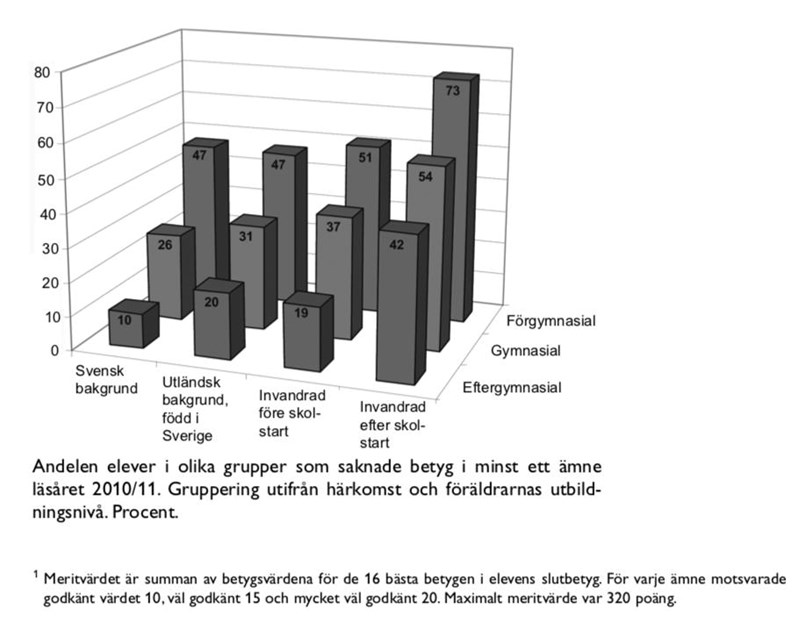
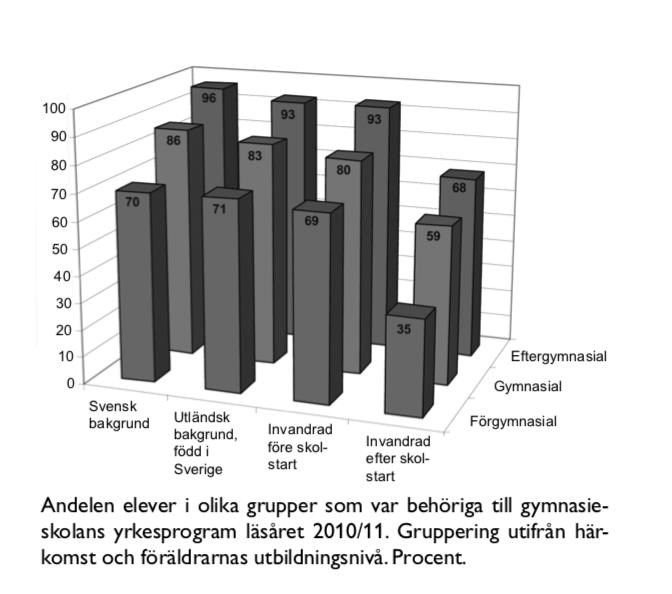
35. Vilken av nedanstående elevgrupper hade det högsta genomsnittliga meritvärdet?
A: Svensk bakgrund där föräldrarna hade förgymnasial utbildning
B: Utländsk bakgrund, född i Sverige där föräldrarna hade gymnasial utbildning
C: Invandrad före skolstart där föräldrarna hade förgymnasial utbildning
D: Invandrad efter skolstart där föräldrarna hade eftergymnasial utbildning
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
I denna diagramserie är den primära uppgiften att hitta rätt i det aningen snurriga diagrammet. För att minska förvirring, markera alla alternativ:
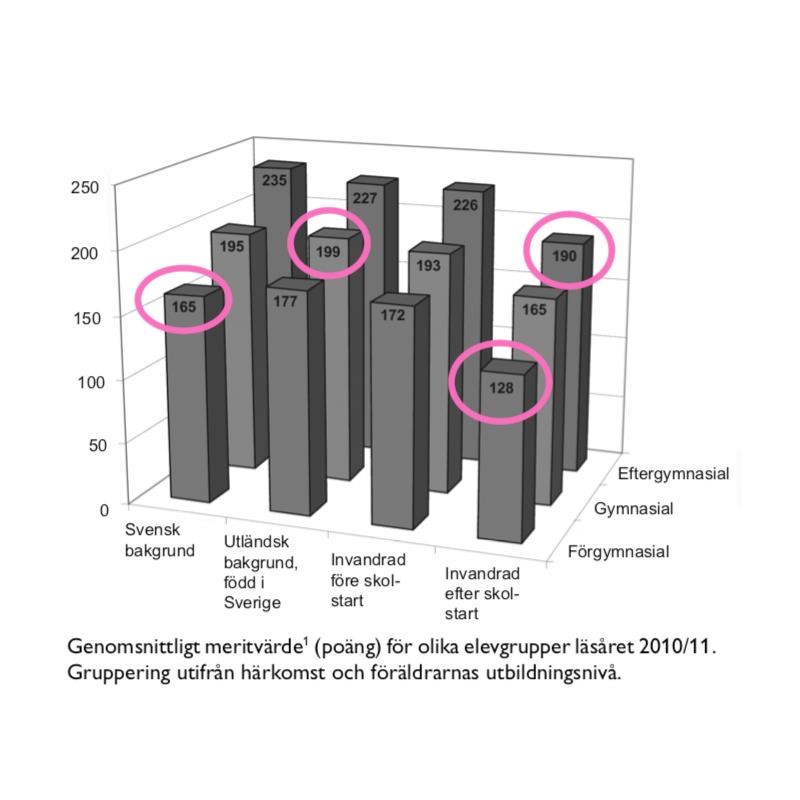
Den högsta siffran är 199, tillhörande "Utländsk bakgrund, född i Sverige där föräldrarna hade gymnasial utbildning".
Svar: B, Utländsk bakgrund, född i Sverige där föräldrarna hade gymnasial utbildning.
36. Studera andelen elever som saknade betyg i minst ett ämne. Hur stor var skillnaden mellan elevgruppen med svensk bakgrund där föräldrarna hade förgymnasial utbildning och elevgruppen med utländsk bakgrund, född i Sverige där föräld rarna hade gymnasial utbildning?
A: 10 procentenheter
B: 13 procentenheter
C: 16 procentenheter
D: 21 procentenheter
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Markera grupperna i diagrammet:
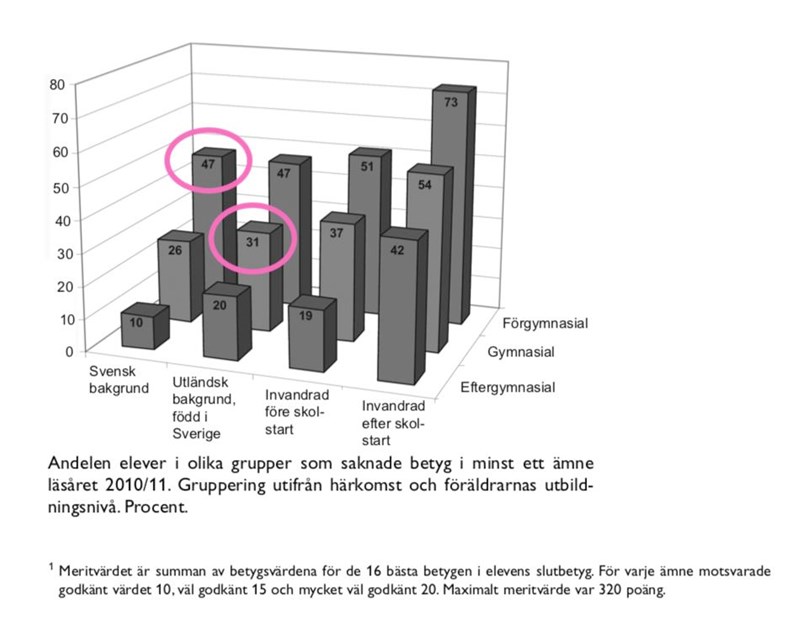
Notera att siffrorna här är angivna i procent. Eftersom vi letar efter en skillnad i procentenheter innebär det bara att ta den ena siffran minus den andra, .
Svar: C, 16 procentenheter.
37. Hur många i elevgruppen invandrad efter skolstart där föräldrarna hade efter gymnasial utbildning var behöriga till gymnasieskolans yrkesprogram?
A: En av tre
B: Två av fem
C: Tre av fem
D: Två av tre
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Identifiera gruppen i diagrammet:
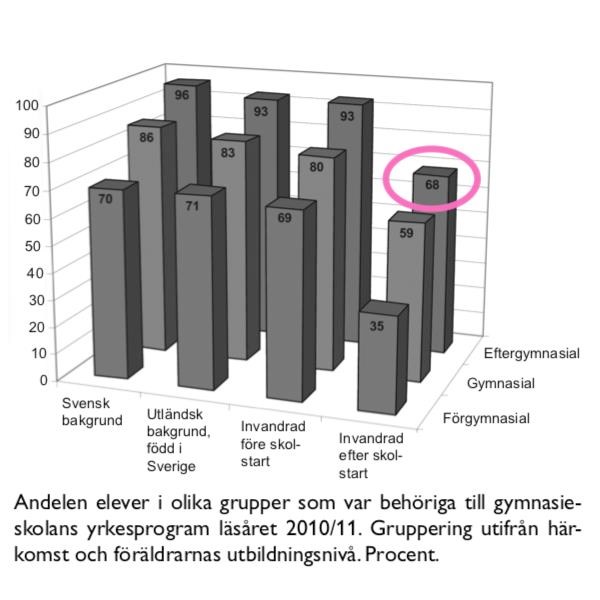
Även här är resultatet angivet i andelar, vilket innebär att 68% ska omvandlas till ett bråk. 66,666...% är samma som två tredjedelar, och 68% är väldigt nära denna siffra.
Svar: D, Två av tre.
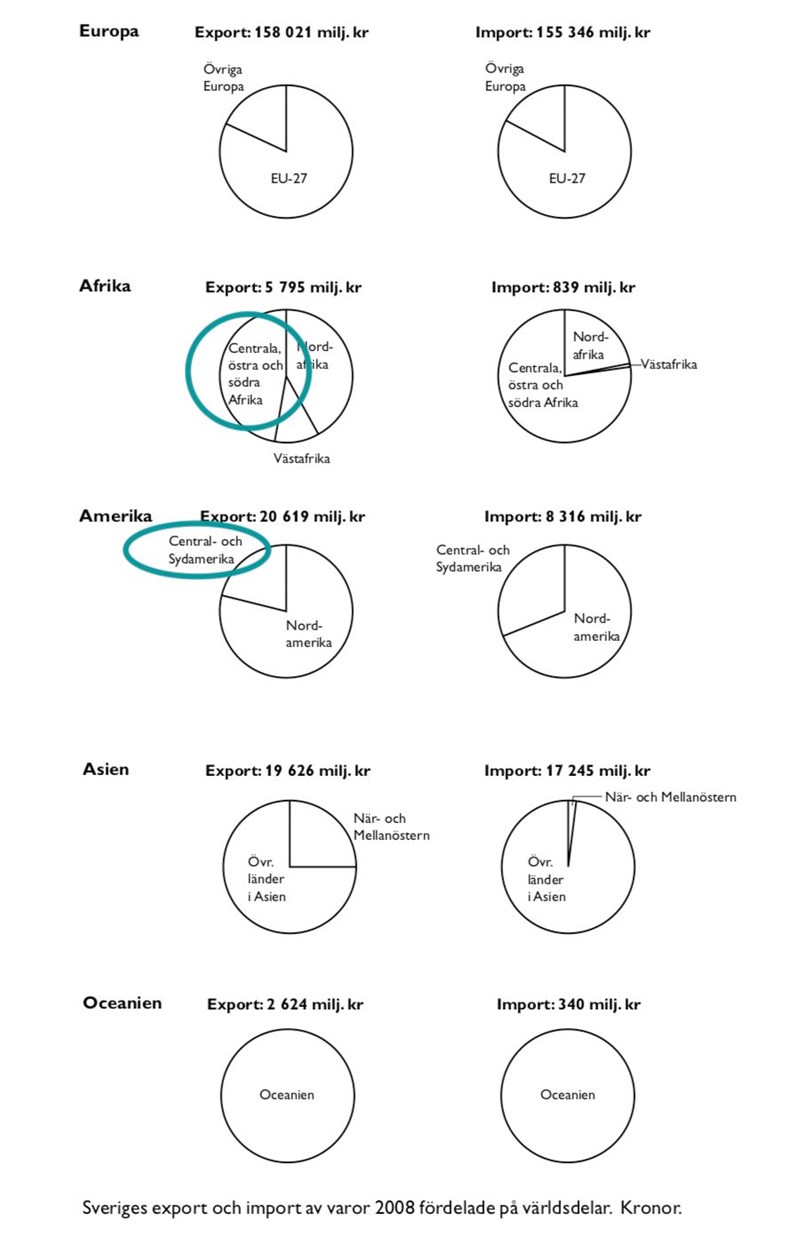
Export och import av varor: (38 - 40)
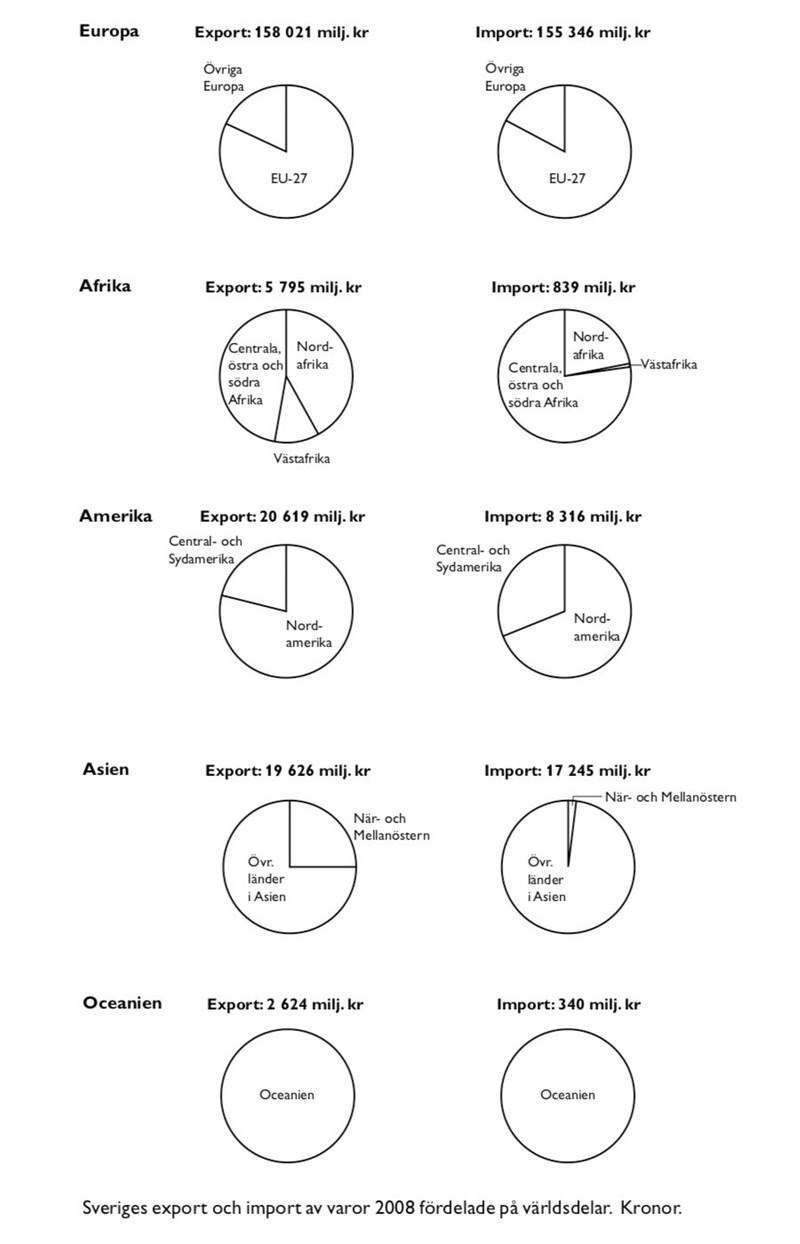
38. Vart exporterade Sverige varor till ett värde av 4 900 miljoner kr?
A: Övriga Europa
B: Nordafrika
C: Centrala, östra och södra Afrika
D: När- och Mellanöstern
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Avrunda 4 900 miljoner kr till 5 000 miljoner kronor, då blir det lättare att räkna. Markera sedan alternativen i diagrammet:
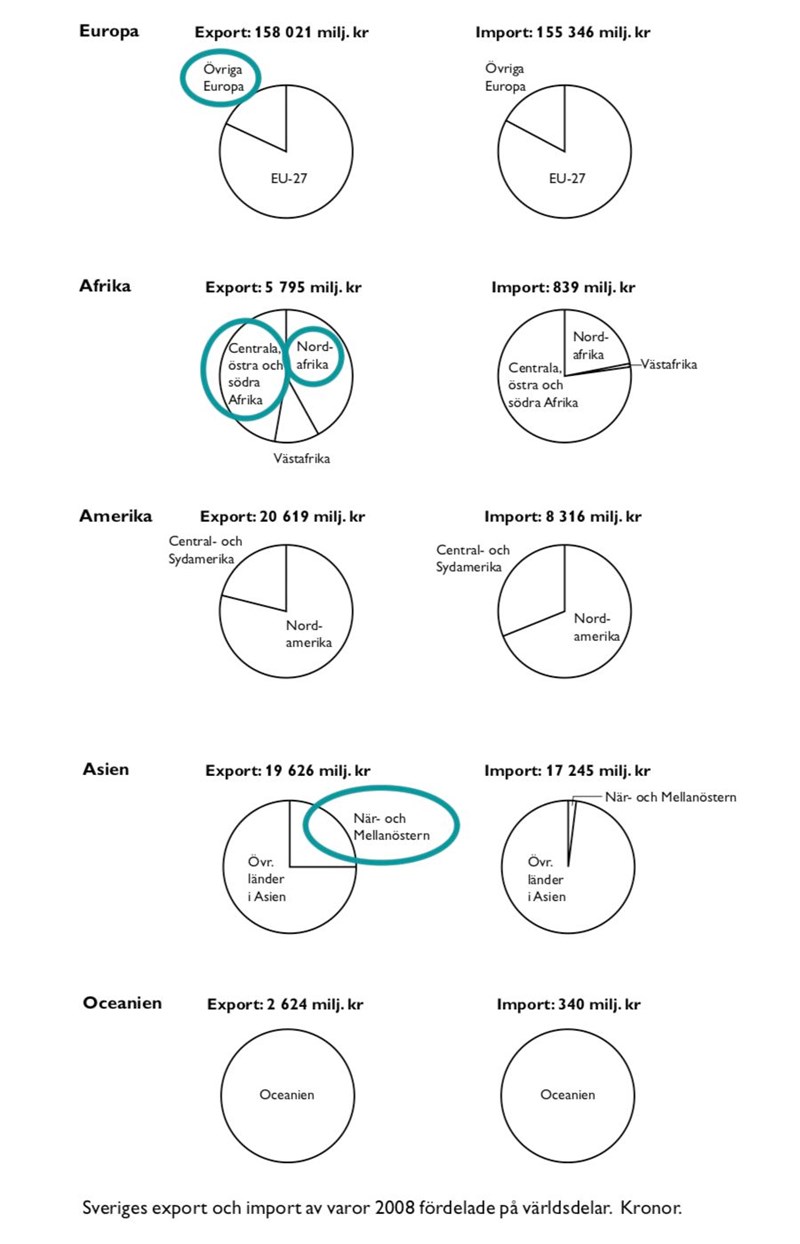
Sverige exporterade varor för knappt 6000 miljoner till Afrika, och varken Centrala, östra och södra Afrika eller Nordafrika är mer än hälften av exporten. Alltså kan denna export maximalt stå för 3000 miljoner, vilket är långt under den sökta siffran. Då kan alternativ B och C uteslutas. Övriga Europa tycks stå för ungefär en femtedel av den totala exporten till Europa, som är 158 021 miljoner, alltså långt över de 5000 miljoner som eftersöks. Kvar blir då alternativ D, När- och Mellanöstern, som utgör en fjärdedel av drygt 20 000 miljoner, vilket är väldigt nära den eftersökta siffran.
Svar: D, När- och Mellanöstern.
39. Hur stor var skillnaden mellan värdet av Sveriges totala export och värdet av Sveriges totala import?
A: 2 700 miljoner kr
B: 24 600 miljoner kr
C: 85 400 miljoner kr
D: 136 300 miljoner kr
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Att räkna ihop de två kolumnerna tar alldeles för lång tid. Räkna istället skillnaden mellan export och import, och summera den siffran istället. Var noga med vilka tal som är positiva/negativa! Var inte rädd för att avrunda siffrorna. Svarsalternativen är långt ifrån varandra. Så länge du avrundar korrekt finns det ingen risk för att få fel svar.
Export - Import: (milj. kr)
Europa: 3 000
Afrika: 5 000
Amerika: 12 000
Asien: 2 000
Oceanien: 2 000
Summa: .
Svar: B, 24 600 miljoner kr.
40. Jämför importen från centrala, östra och södra Afrika med importen från Central- och Sydamerika. Hur stor var skillnaden i kronor räknat?
A: 400 miljoner kr
B: 650 miljoner kr
C: 1 300 miljoner kr
D: 1 950 miljoner kr
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Markera de relevanta siffrorna:
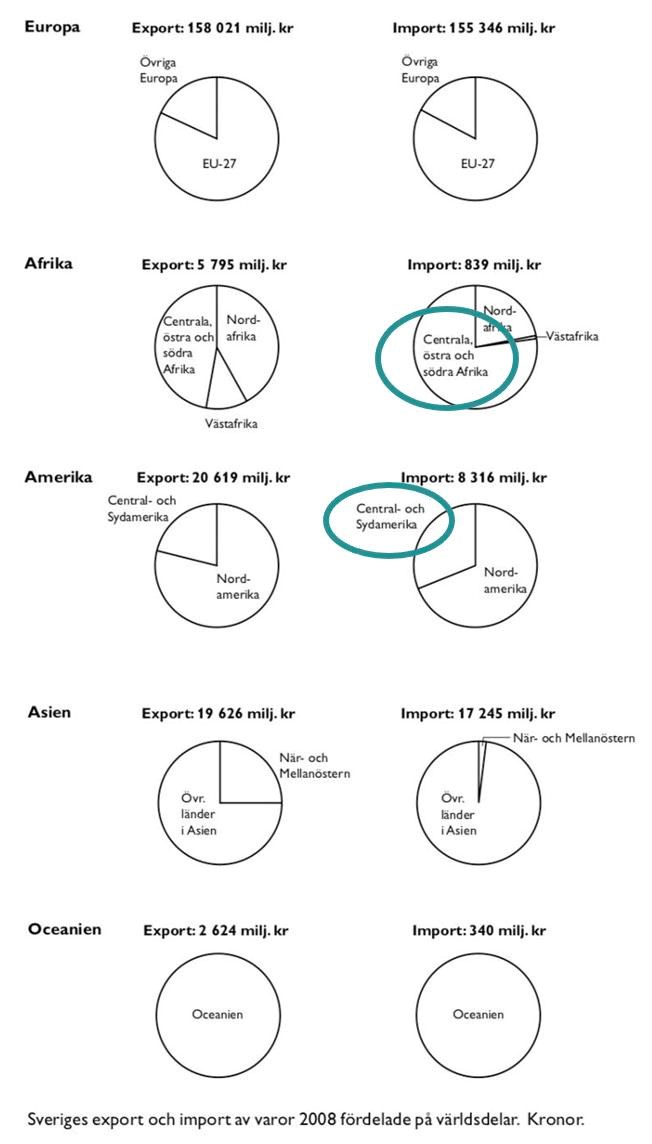
Centrala, östra och södra Afrika utgör drygt tre fjärdedelar av 850 miljoner kronor (eftersom andelen avrundas nedåt avrundas beloppet uppåt), vilket motsvarar drygt miljoner kronor. Central- och Sydamerika utgör mellan en dryg tredjedel av cirka 8300 miljoner kr (eftersom andelen är avrundad uppåt bör totalsiffran avrundas nedåt), vilket motsvarar miljoner kronor.
2 000 miljoner kronor ligger närmast alternativ D, 1 950 miljoner kr.
Svar: D, 1 950 miljoner kr.
EDIT: Detta svar har bytts ut, då det tidigare utgick från regionernas exporter, istället för importer. Varmt tack till fsjodal som påpekat detta längre ned i tråden! :)
Smutstvätt skrev:12. Vilket svarsalternativ är ett heltal?
A:
B:
C:
D:
Summan av A och B kommer aldrig att bli heltal. Decimalerna tar inte ut varandra. Då kvarstår C och D som möjliga alternativ. C är lika med . Eftersom detta tal inte kan skrivas som något tal x dividerat med tre, , kommer trean inte att göra talet till ett heltal.
Då kvarstår endast D, vilket är det korrekta alternativet. För den som vill beräkna D är den potenslag som säger att mycket användbar. , och roten ur nio är lika med tre, ett heltal.
Något vagt, kan hållas mera stringent med fokus på irrationella tal.
Trinity skrev:Smutstvätt skrev:12. Vilket svarsalternativ är ett heltal?
A:
B:
C:
D:
Summan av A och B kommer aldrig att bli heltal. Decimalerna tar inte ut varandra. Då kvarstår C och D som möjliga alternativ. C är lika med . Eftersom detta tal inte kan skrivas som något tal x dividerat med tre, , kommer trean inte att göra talet till ett heltal.
Då kvarstår endast D, vilket är det korrekta alternativet. För den som vill beräkna D är den potenslag som säger att mycket användbar. , och roten ur nio är lika med tre, ett heltal.Något vagt, kan hållas mera stringent med fokus på irrationella tal.
Jag håller med om att detta inte är trådens bästa förklaring. Skriv gärna en alternativ variant här i tråden! :)
Det enda man behöver veta är att är ett irrationellt tal och att även om man multiplicerar/adderar/subtraherar detta med ett rationellt tal blir resultatet fortfarande irrationellt och därmed inte ett heltal.
Detta är HP och att snabbt kunna få fram vilket svarsalternativ som är rätt har betydelse. Smutstvätts tankegång är rätt snabb och svaret blir rätt.
Om man har lite mer tid så kan man:
A: alltså irrationellt, alltså inte heltal
B: på samma sätt som A
C: alltså irrationellt, alltså inte ett heltal
D:
Snabbhet på HP kan vara önskvärt. Det är ett mycket besynnerligt prov och enl. mig utan något större värde. Men det finns, inte att göra så mycket åt det.
Snabb översikt så inser man att D ger svaret 3 och därmed behöver man inte befatta sig med irrationella tal alls. Men om man vill ha ett stringent resonemang är ovanstående 'post' bra. Är man snabb tar det ingen lång tid. Räkningarna är triviala. Goda baskunskaper slår "street smart" vilken dag som helst i veckan.
Smutstvätt skrev:25. En affär säljer strömbrytare styckvis. Om man köper färre än tio så gäller ett visst pris, och om man köper tio eller fler så får man 8 % rabatt på det totala priset. Hur mycket kostar det att köpa 16 strömbrytare vid ett och samma tillfälle?
(1) Det kostar 479,20 kr att köpa 8 strömbrytare.
(2) Om man köper 10 strömbrytare så får man 47,92 kr i rabatt.
Tillräcklig information för lösningen erhålls
A i (1) men ej i (2)
B i (2) men ej i (1)
C i (1) tillsammans med (2)
D i (1) och (2) var för sig
E ej genom de båda påståendena(1): Vi kan beräkna priset av en strömbrytare med denna information. Multiplikation av styckpriset med 16, tillsammans med att det är givet att vi får åtta procent rabatt, ger totalpriset för 16 strömbrytare. (1) är alltså tillräckligt.
(2): Vi vet att rabatten är 47,92 kronor, och att detta motsvarar åtta procent av totalpriset. Vi kan då beräkna det totala priset och få ut ett styckpris. Det kan användas för att beräkna totalpriset, och (2) är alltså tillräckligt med information.
Svar: D, i (1) och (2) var för sig
Hur gör man för att räkna fram vad styckpriset blir per strömbrytare när man endast har informationen i (2)?
Har du tänkt på att man i båda fallen har tillgång till upplysningarna i själva frågan också?
Smutstvätt skrev:16. x och y är två på varandra följande heltal sådana att .
Kvantitet I: 2x
Kvantitet II: Summan av x och y
A: I är större än II
B: II är större än I
C: I är lika med II
D: Informationen är otillräckligBörja med att gissa ett förhållande, säg att I > II. Vi ställer upp det:
, vilket inte är sant. Vi vet att x < y. Då vet vi att II > I, men den som känner sig osäker kan gärna testa detta påstående:
, vilket är korrekt enligt informationen från uppgiften.
Svar: B, II är större än I.
Om y följer x så är y=x+1. Då är x+y=2x+1.
Tack igen för trådarna =)
Smutstvätt skrev:Export och import av varor: (38 - 40)
38. Vart exporterade Sverige varor till ett värde av 4 900 miljoner kr?
A: Övriga Europa
B: Nordafrika
C: Centrala, östra och södra Afrika
D: När- och Mellanöstern- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Avrunda 4 900 miljoner kr till 5 000 miljoner kronor, då blir det lättare att räkna. Markera sedan alternativen i diagrammet:
Sverige exporterade varor för knappt 6000 miljoner till Afrika, och varken Centrala, östra och södra Afrika eller Nordafrika är mer än hälften av exporten. Alltså kan denna export maximalt stå för 3000 miljoner, vilket är långt under den sökta siffran. Då kan alternativ B och C uteslutas. Övriga Europa tycks stå för ungefär en femtedel av den totala exporten till Europa, som är 158 021 miljoner, alltså långt över de 5000 miljoner som eftersöks. Kvar blir då alternativ D, När- och Mellanöstern, som utgör en fjärdedel av drygt 20 000 miljoner, vilket är väldigt nära den eftersökta siffran.
Svar: D, När- och Mellanöstern.
39. Hur stor var skillnaden mellan värdet av Sveriges totala export och värdet av Sveriges totala import?
A: 2 700 miljoner kr
B: 24 600 miljoner kr
C: 85 400 miljoner kr
D: 136 300 miljoner kr- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Att räkna ihop de två kolumnerna tar alldeles för lång tid. Räkna istället skillnaden mellan export och import, och summera den siffran istället. Var noga med vilka tal som är positiva/negativa! Var inte rädd för att avrunda siffrorna. Svarsalternativen är långt ifrån varandra. Så länge du avrundar korrekt finns det ingen risk för att få fel svar.
Export - Import: (milj. kr)
Europa: 3 000
Afrika: 5 000
Amerika: 12 000
Asien: 2 000
Oceanien: 2 000Summa: .
Svar: B, 24 600 miljoner kr.
40. Jämför importen från centrala, östra och södra Afrika med importen från Central- och Sydamerika. Hur stor var skillnaden i kronor räknat?
A: 400 miljoner kr
B: 650 miljoner kr
C: 1 300 miljoner kr
D: 1 950 miljoner kr- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Markera de relevanta siffrorna:
Centrala, östra och södra Afrika är strax hälften av cirka 5 800 miljoner kr, vilket motsvarar drygt 2 700 miljoner kr. Central- och Sydamerika utgör strax under en fjärdedel av cirka 20 miljoner kr (eftersom andelen är avrundad uppåt bör totalsiffran avrundas nedåt), vilket är lite under 5 000 miljoner kr, säg 4 700 miljoner kr.
2 000 miljoner kronor ligger närmast alternativ D, 1 950 miljoner kr.
Svar: D, 1 950 miljoner kr.
Hej! Varför räknar man på Sveriges export till centrala, östra och södra Afrika, samt Central- och Sydamerika när det tydligt står "import från..." i fråga 40? Har jag missat något helt? Jag förstår ju absolut att svaret blir rätt med de siffrorna men varför är frågan då ställd på det viset?
Tack på förhand!
Utmärkt fråga! 
Nu är lösningen ändrad till att fokusera på import, istället för export. Tack så mycket för din skarpa observation, och säg gärna till om du hittar fler tokigheter! :)
Hej! Kan du förklara fråga 8 lite mer? Jag trodde att pythagoras sats utgick ifrån a^2+b^2=c^2 men i lösningen står det 5^2-4^2 och jag förstår inte varför det blir minus och inte plus...
seast002 skrev:Hej! Kan du förklara fråga 8 lite mer? Jag trodde att pythagoras sats utgick ifrån a^2+b^2=c^2 men i lösningen står det 5^2-4^2 och jag förstår inte varför det blir minus och inte plus...
Det stämmer men höjden är en katet så det man gör är att subtrahera en katet från båda led så att den andra är ensam kvar i ett led:
c^2-b^2=a^2