How many min-o-max måste jag rippa ... 2.

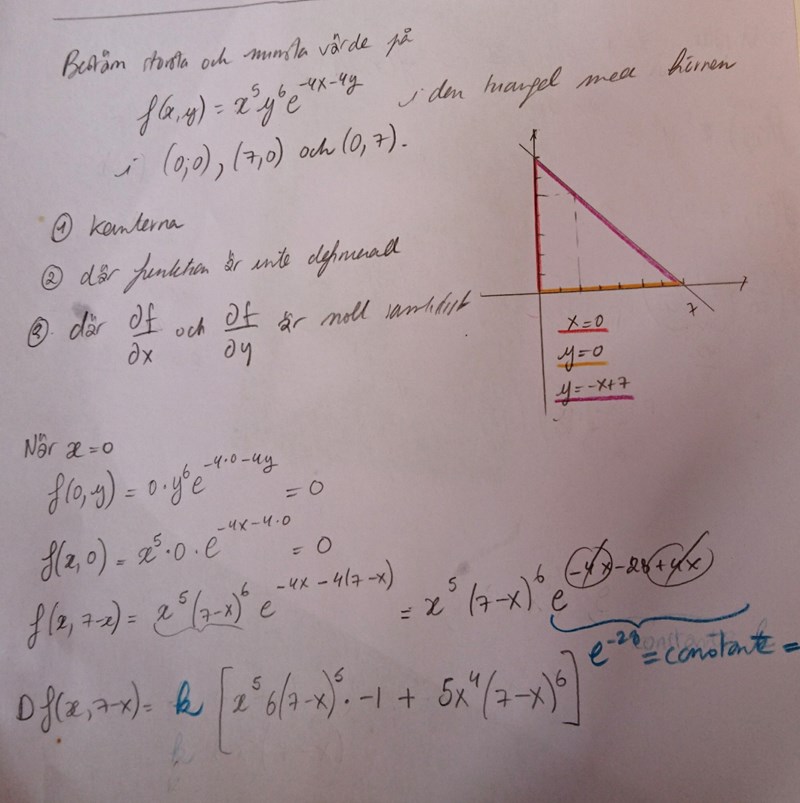
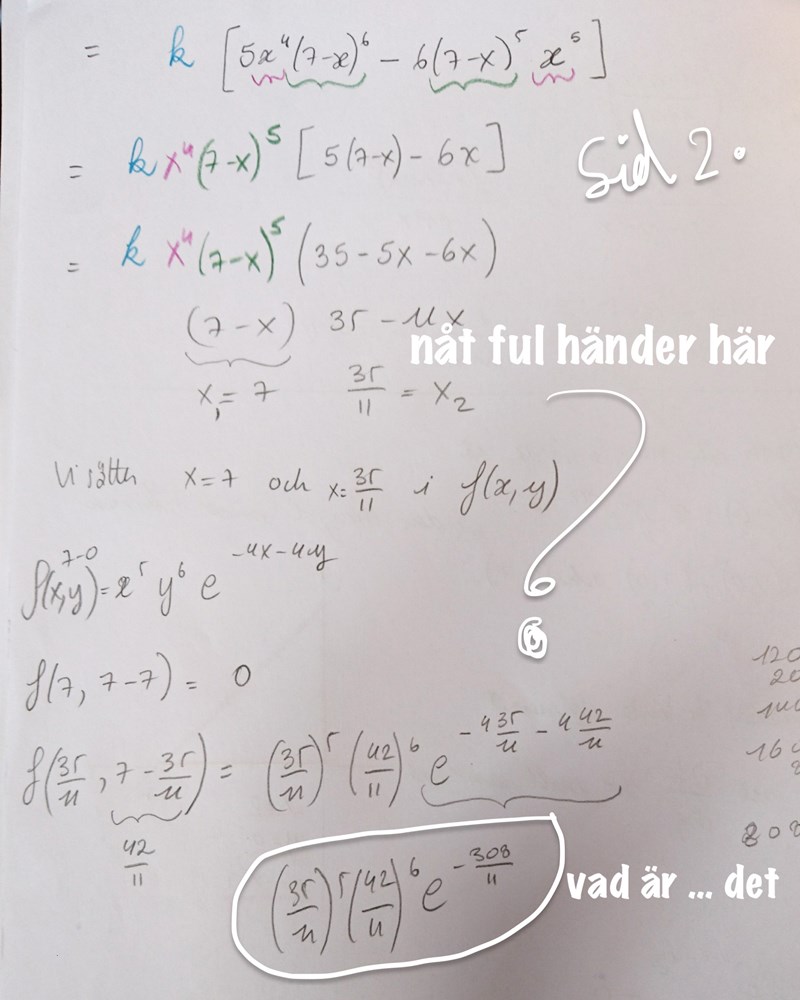
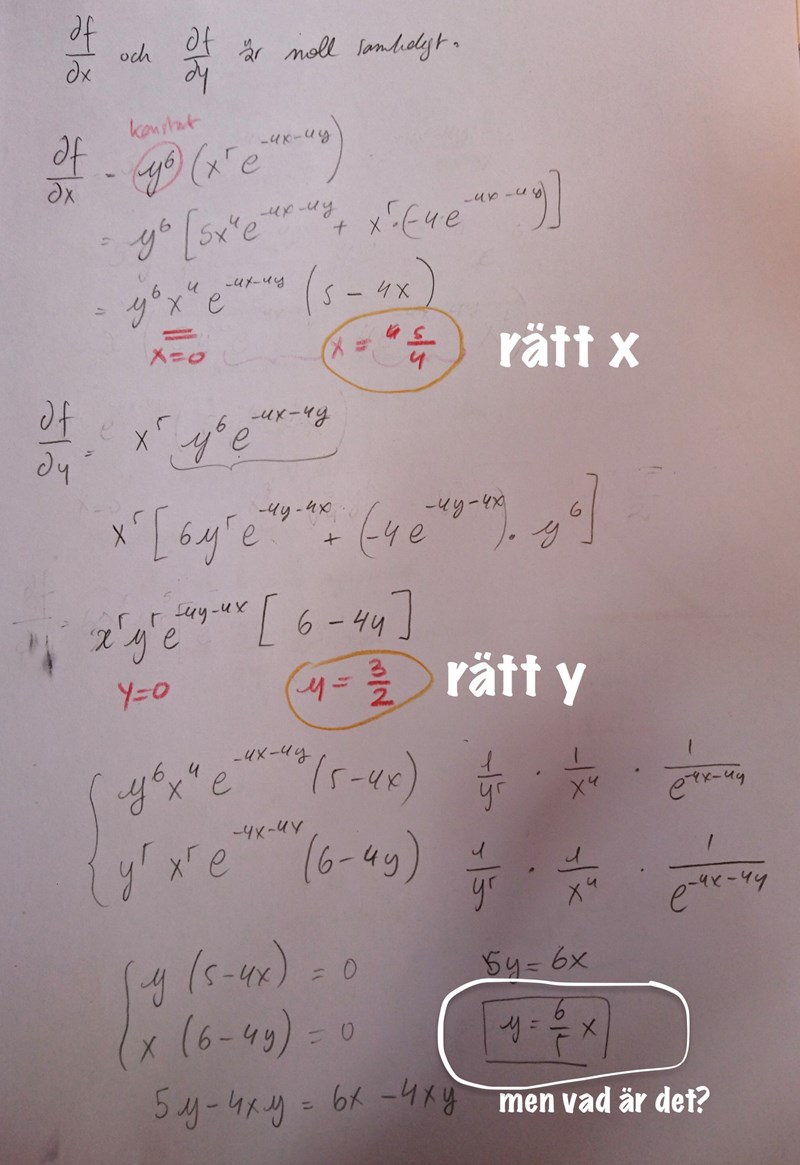
Den här uppgiften kan verka lite klurig att tolka, men den gör faktiskt beräkningarna enklare. De partiella derivatorna blir ju:

$\dfrac{\partial f}{\partial x}=5x^4y^6e^{-4x-4y}-4x^5y^6e^{-4x-4y}$

$\dfrac{\partial f}{\partial y}=6x^5y^5e^{-4x-4y}-4x^5y^6e^{-4x-4y}$

Vi börjar med att undersöka när $x$-derivatan är noll:

$5x^4y^6e^{-4x-4y}-4x^5y^6e^{-4x-4y}=0$

$e^{-4x-4y}(5x^4y^6-4x^5y^6)=0$

$e^{k}$ är aldrig noll för reella $k$ så den faktorn kan vi ignorera:

$x^4y^6(5-4x)=0$

Enligt nollproduktmetoden ger detta lösningarna:

$x=0$

$y=0$

$x=\frac{5}{4}$

Gör vi samma sak på $y$-derivatan får vi lösningarna:

$x=0$

$y=0$

$y=\frac{3}{2}$

Eftersom $x=0$ och $y=0$ gör att båda derivatorna med noll räcker det med att antingen $x$ eller $y$ är noll. $(x,0)$ och $(0,y)$ är således kritiska punkter för alla $x$ och $y$. Det som är extra intressant är att dessa sammanfaller med triangelns $x$- och $y$-katetrar (på intervallet som de gäller för), och alltså kan vi strunta i dessa eftersom vi ändå kommer att beräkna största och minsta värde på randen senare.

Den enda kritiska punkten som behöver undersökas är då $(\frac{5}{4}, \frac{3}{2})$. $y=\frac{6}{5}x$-punkten fattar jag inte riktigt var du får ifrån.

På randpunkterna har du gjort i stort sätt rätt.

$(\frac{35}{11})^5(\frac{42}{11})^6e^{-\frac{308}{11}}$-punkten kan du analysera närmare genom att använda dig av andraderivatorna.

Du har även glömt att $x=0$ är en lösning i $x^4(7-x)^5(35-11x)=0$-ekvationen.

AlvinB skrev:

Den här uppgiften kan verka lite klurig att tolka, men den gör faktiskt beräkningarna enklare. De partiella derivatorna blir ju:

$\dfrac{\partial f}{\partial x}=5x^4y^6e^{-4x-4y}-4x^5y^6e^{-4x-4y}$

$\dfrac{\partial f}{\partial y}=6x^5y^5e^{-4x-4y}-4x^5y^6e^{-4x-4y}$

Vi börjar med att undersöka när $x$-derivatan är noll:

$5x^4y^6e^{-4x-4y}-4x^5y^6e^{-4x-4y}=0$

$e^{-4x-4y}(5x^4y^6-4x^5y^6)=0$

$e^{k}$ är aldrig noll för reella $k$ så den faktorn kan vi ignorera:

$x^4y^6(5-4x)=0$

Enligt nollproduktmetoden ger detta lösningarna:

$x=0$

$y=0$

$x=\frac{5}{4}$

Okay...  Här. Varför y=0? Vi undersöker ju med avseende på x?

Är inte y en konstant?

Gör vi samma sak på $y$-derivatan får vi lösningarna:

$x=0$

$y=0$

$y=\frac{3}{2}$

Samma fråga,men för x...

Eftersom $x=0$ och $y=0$ gör att båda derivatorna med noll räcker det med att antingen $x$ eller $y$ är noll. $(x,0)$ och $(0,y)$ är således kritiska punkter för alla $x$ och $y$. Det som är extra intressant är att dessa sammanfaller med triangelns $x$- och $y$-katetrar (på intervallet som de gäller för), och alltså kan vi strunta i dessa eftersom vi ändå kommer att beräkna största och minsta värde på randen senare.

Den enda kritiska punkten som behöver undersökas är då $(\nicefrac{5}{4}, \nicefrac{3}{2})$.

Men varför just den?

$y=\frac{6}{5}x$-punkten fattar jag inte riktigt var du får ifrån.

Igenom att lösa ekvationen, men jag håller med. Det är en mystery.

På randpunkterna har du gjort i stort sätt rätt.

$(\frac{35}{11})^5(\frac{42}{11})^6e^{-\frac{308}{11}}$-punkten kan du analysera närmare genom att använda dig av andraderivatorna.

Du har även glömt att $x=0$ är en lösning i $x^4(7-x)^5(35-11x)=0$-ekvationen.

dajamanté skrev:

AlvinB skrev:

Den här uppgiften kan verka lite klurig att tolka, men den gör faktiskt beräkningarna enklare. De partiella derivatorna blir ju:

$\dfrac{\partial f}{\partial x}=5x^4y^6e^{-4x-4y}-4x^5y^6e^{-4x-4y}$

$\dfrac{\partial f}{\partial y}=6x^5y^5e^{-4x-4y}-4x^5y^6e^{-4x-4y}$

Vi börjar med att undersöka när $x$-derivatan är noll:

$5x^4y^6e^{-4x-4y}-4x^5y^6e^{-4x-4y}=0$

$e^{-4x-4y}(5x^4y^6-4x^5y^6)=0$

$e^{k}$ är aldrig noll för reella $k$ så den faktorn kan vi ignorera:

$x^4y^6(5-4x)=0$

Enligt nollproduktmetoden ger detta lösningarna:

$x=0$

$y=0$

$x=\frac{5}{4}$

Okay...  Här. Varför y=0? Vi undersöker ju med avseende på x?

Är inte y en konstant?

Gör vi samma sak på $y$-derivatan får vi lösningarna:

$x=0$

$y=0$

$y=\frac{3}{2}$

Samma fråga,men för x...

Det jag gör är att jag löser ekvationerna

$5x^4y^6e^{-4x-4y}-4x^5y^6e^{-4x-4y}=0$

$6x^5y^5e^{-4x-4y}-4x^5y^6e^{-4x-4y}=0$

Som jag visade i originalinlägget faktoriserar jag dessa och använder nollproduktmetoden för att utläsa när de blir noll. Det är fullt tillåtet för ett visst $y$-värde att göra så att $x$-derivatan blir noll (eller tvärtom) eftersom $x$-derivatan innehåller $y$-termer.

Eftersom $x=0$ och $y=0$ gör att båda derivatorna med noll räcker det med att antingen $x$ eller $y$ är noll. $(x,0)$ och $(0,y)$ är således kritiska punkter för alla $x$ och $y$. Det som är extra intressant är att dessa sammanfaller med triangelns $x$- och $y$-katetrar (på intervallet som de gäller för), och alltså kan vi strunta i dessa eftersom vi ändå kommer att beräkna största och minsta värde på randen senare.

Den enda kritiska punkten som behöver undersökas är då $(\nicefrac{5}{4}, \nicefrac{3}{2})$.

Men varför just den?

Latex-krånglet gjorde det otydligt, men jag menade

$(\dfrac{5}{4},\dfrac{3}{2})$

Denna punkt fås ju eftersom $x=\frac{5}{4}$ gör att $x$-derivatan blir noll och $y=\frac{3}{2}$ gör att $y$-derivatan blir noll (enligt lösningarna på ekvationerna vi skrev upp).

$y=\frac{6}{5}x$-punkten fattar jag inte riktigt var du får ifrån.

Igenom att lösa ekvationen, men jag håller med. Det är en mystery.

 Okej, jag kollade lite närmare på ditt papper. Du försöker alltså lösa

$\left\{\begin{array}{l}y(5-4x)=0\\ x(6-4y)=0\end{array}\right.$

Med hjälp av subsitutionsmetoden. Då får du komma ihåg att du letar efter den specifika lösningen till detta ekvationssystem, och när du löst ut att $y=\frac{6}{5}x$ måste du sätta in det i ekvationerna igen för att få ut lösningen:

$x(6-4(\frac{6}{5}x))=0$

$x(6-\frac{24}{5}x)=0$

$6x(1-\frac{4}{5}x)=0$

Vilket ger lösningarna $x=0$ och $x=\frac{5}{4}$.

Sätter man sedan in $x=0$ och $x=\frac{5}{4}$ i $y(5-4x)=0$ får man $y=0$ och $y=\frac{3}{2}$. Det här är alltså ett annat (krångligare) sätt att komma fram till lösningarna vi redan har.

Igenom att lösa ekvationen, men jag håller med. Det är en mystery.

Genom (inte igenom) att lösa vilken ekvation?

Hej!

Det är enklare att bestämma extremvärden för funktionens logaritm.

    $\displaystyle \ln f(x,y) = 5\ln x + 6\ln y -4(x+y).$

Gradienten till denna funktion är

    $\displaystyle (\nabla \ln f)(x,y)=(\frac{5}{x}-4,\frac{6}{y}-4).$

Gradienten är lika med nollvektorn precis när $(x,y)=(1.25,1.5)$ och denna punkt ligger i det inre av triangeln; i denna punkt är $\ln f(1.25,1.5)=5\ln5+6\ln6-11(\ln4-1).$

Albiki skrev:

Hej!

Det är enklare att bestämma extremvärden för funktionens logaritm.

    $\displaystyle \ln f(x,y) = 5\ln x + 6\ln y -4(x+y).$

Gradienten till denna funktion är

    $\displaystyle (\nabla \ln f)(x,y)=(\frac{5}{x}-4,\frac{6}{y}-4).$

Gradienten är lika med nollvektorn precis när $(x,y)=(1.25,1.5)$ och denna punkt ligger i det inre av triangeln; i denna punkt är $\ln f(1.25,1.5)=5\ln5+6\ln6-11(\ln4-1).$

....

O....M....G!

EDIT: En sak bara.... jag har inte gått igenom gradient grejen. Hur går du från ln linjen till nabla linjen?

AlvinB skrev:

Det jag gör är att jag löser ekvationerna

$5x^4y^6e^{-4x-4y}-4x^5y^6e^{-4x-4y}=0$

$6x^5y^5e^{-4x-4y}-4x^5y^6e^{-4x-4y}=0$

Som jag visade i originalinlägget faktoriserar jag dessa och använder nollproduktmetoden för att utläsa när de blir noll. Det är fullt tillåtet för ett visst $y$-värde att göra så att $x$-derivatan blir noll (eller tvärtom) eftersom $x$-derivatan innehåller $y$-termer.

 

Ok, det måste jag meditera på några timmar tilll. Jag trodde att när vi deriverar med avseende på $x$ frågade vi ingenting om $y$ eftersom $y$ var då konstant.

Latex-krånglet gjorde det otydligt, men jag menade

$(\dfrac{5}{4},\dfrac{3}{2})$

Just det, för vi har redan undersökt fällena där $x=0$ och $y=0$.

Denna punkt fås ju eftersom $x=\frac{5}{4}$ gör att $x$-derivatan blir noll och $y=\frac{3}{2}$ gör att $y$-derivatan blir noll (enligt lösningarna på ekvationerna vi skrev upp).

 Okej, jag kollade lite närmare på ditt papper. Du försöker alltså lösa

$\left\{\begin{array}{l}y(5-4x)=0\\ x(6-4y)=0\end{array}\right.$

Med hjälp av subsitutionsmetoden. Då får du komma ihåg att du letar efter den specifika lösningen till detta ekvationssystem, och när du löst ut att $y=\frac{6}{5}x$ måste du sätta in det i ekvationerna igen för att få ut lösningen:

$x(6-4(\frac{6}{5}x))=0$

$x(6-\frac{24}{5}x)=0$

$6x(1-\frac{4}{5}x)=0$

Vilket ger lösningarna $x=0$ och $x=\frac{5}{4}$.

Sätter man sedan in $x=0$ och $x=\frac{5}{4}$ i $y(5-4x)=0$ får man $y=0$ och $y=\frac{3}{2}$. Det här är alltså ett annat (krångligare) sätt att komma fram till lösningarna vi redan har.

 Tack, nu förstår jag. Eftersom jag visste inte vad jag höll på med jag bara inte fortsatt...

@Smaragdalena: jag menade den här ekvation övan!