Hur beräknar jag perioden av denna funktion
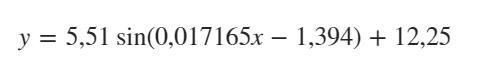
Skulle någon även kunna förklara varför man inte tar 2*pi/A
Vad är A?
Vad är perioden för en helt vanlig sin(x)?
Laguna skrev:Vad är A?
Vad är perioden för en helt vanlig sin(x)?
A amplitud,
2pi
Amplituden har ingenting alls med perioden att göra. Jämför t.ex. sin(x) med 2sin(x).
Laguna skrev:Amplituden har ingenting alls med perioden att göra. Jämför t.ex. sin(x) med 2sin(x).
okej ser det genom grafiskt verktyg, men hur beräknas perioden då?
Det står säkert bra saker i din bok, som jag skulle kunna förklara om de är otydliga, men här är svaret: sin(ax+b) har perioden 2pi/a.
Laguna skrev:Det står säkert bra saker i din bok, som jag skulle kunna förklara om de är otydliga, men här är svaret: sin(ax+b) har perioden 2pi/a.
jag tänker att 2pi är 360 grader i radianer sedan delas den faktorn på nå sätt så den visar vart sin blir sig likt.
En "vanlig" sinusfunktion sin(x) går ett varv på ett varv, d v s på 360o eller 2pi radianer. Om en sinusfunktion går snabbare eller långsammare än sin(x) så behöver man justera detta med hjälp av en faktor a, så att funktionen är sin(ax) istället. Om man vet a och vill veta perioden, d v s hur lång tid det tar för den snabbare/långsammare funktionen att gå ett varv, s är det väl inte så konstigt att "ett varv" mätt i antingen grader eller radianer dyker upp i uttrycket?



