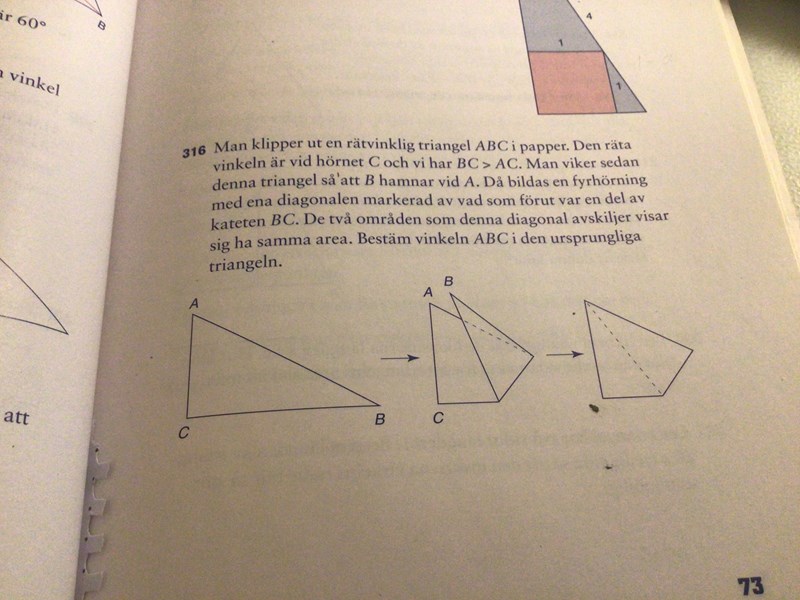
Hur bestämma <ABC ?
Arup skrev:
Det vore mycket enklare för oss som svarar om du lägger uppgiften på en lämplig nivå, så att vi vet om man t ex får använda trigonometri när man löser uppgiften.
Om vi kallar "vikpunkten" bredvid hörn A för D och hörnet längst till höger för E, så vet vi att arean för triangeln ABC är en tre gånger så stor som arean ACD = arean ADE. Det betyder att |BC| = 3 |CD| och att |AD| = 2 |CD|. Alltså är triangeln ACD "en halv liksidig triangel". Du kan antingen använda detta faktum eller Pythagoras sats för att beräkna |AC| (jag skulle sätta |BC| = 3 för att få enkla siffror att räkna med).
Kommer du vidare härifrån?
jag vet ej vilken nivå problemet är lämplig för så det var därför jag lade upp problemet i allmänna diskussioner. Men, jag skulle tro att det går att lösa mha matte 2 kunskaper-
Här är en ledtråd för någon. 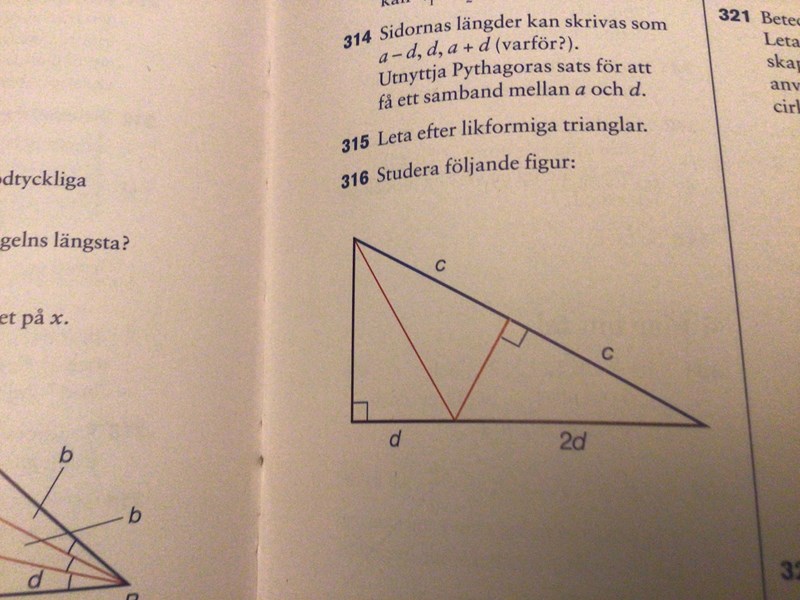
Javisst, så ser det ut när man viker ut pappret igen.
Som Smaragdalena visade har vi en halv liksidig triangel till vänster, alltså med en 60o-vinkel nere till höger.
De andra trianglarna är kongruenta. Alla vinklarna trillar nu ut.
Ok. Har du något bra tips ?
Tips på vilken del?
Som smaragdalena menar . Jag brukar föredra när volontärer rita på papper, eftersom det blir lättare för mig att hänga med
Är du med på att vinkeln där jag skrivit 60o är så stor?
Är du med på att vinklarna som jag markerat som lika stora är lika stora?
Eller ska vi backa längre? Är du med på figurens d, 2d och c?
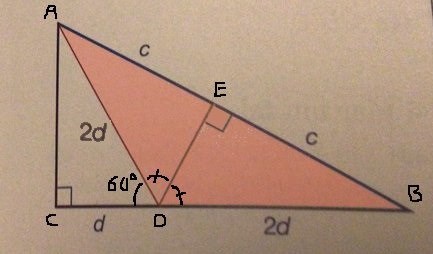
Backa längre
tack
Ok, vi kan ta det från början.
Men jag får återkomma om en stund.
Ok. Kan vi ta om allt från början. Jag uppskattar bilden du visade
Hur blir vinkeln 60˚ Hur kom du fram till det ?
Jag har numrerat stegen så att du kan säga hur långt du är med.
1. De rödtonade trianglarna är kongruenta, eftersom de låg på varandra när pappret var vikt.
2. Det var givet att trianglarna ACD och ADE har samma area. Så alla tre trianglarna har samma area.
3. Triangel ABD har då dubbel area mot ACD.
4. De har samma höjd (AC), vilket ger att BD är dubbelt så lång som CD.
5. Därav sidlängderna 2d (på två sidor pga kongruensen, när pappret var vikt låg BD på AD) respektive d.
6. Titta på triangeln ACD med kort katet d och hypotenusan 2d.
Det innebär att triangeln är en halv liksidig triangel och att vinkel ADC är 60o.
7. Därifrån är det enkelt att beräkna de andra vinklarna.
Är det möjligt att du ritar en bild ?
Alla beteckningar är från bilden i #9.
Har du prövat att klippa ut en triangel och vika den som det sägs i uppgiften?
Först för du hörnet B till hörnet A och håller fast det där. Platta till pappret så att det blir ett veck.
Rita en linje där det är streckat i uppgiftens figur, alltså längs kanten på den vikta delen.
När du viker ut pappret igen ser det ut som i figuren i #9.
AD är strecket du ritade. DE är vikningslinjen.
Figuren i #4 är inte bra ritad. Sträckorna som ska vara lika långa ser inte alls ut att vara det.
Tillägg: 29 mar 2024 09:41
För tydlighetens skull: När du viker ut pappret igen ser det ungefär ut som i figuren i #9.
Det är bara för en speciell triangel som triangeln vänster om strecket är en halv liksidig triangel
med en 60o-vinkel.
louis jag förstår inte
Har du vikt en triangel?
japp
Och ritat strecket? Och vikt ut pappret igen?
Såg det då ut ungefär som figuren i #9?
dock, vet jag ej om jag har vikt pappret rätt
1ja
Kan du ta en bild på pappret och visa?
kan jag återkomma om typ 5 timmar är du tillgänglig då. Jag visar min lösning sedan visar du din. Låter det bra ?
jag måste tyvär gå nu, men skulle vi kunna göra li
te senare ?
Javisst. Fast min lösning visade jag i #14, så när som lite enkel vinkelräkning.
ok, men skulle du kunna visa på ett blankt papper ?
steg för steg ?
I #14 är det steg för steg.
Det viktiga här är att du har testat vikningen och ser att det du får motsvaras av figuren i #9.
Att AD är strecket du ritat och att DE är vecket på pappret.
Visa som sagt din vikning.


