Hur bevisar man gränsvärdet sin(x)/x ---> 1 då x --->0?

Vad är $f(x)$? Påståendet stämmer om exempelvis $f(x)=\sin{x}$, men inte om $f(x)=2x$. :)

Smutstvätt skrev:

Vad är $f(x)$? Påståendet stämmer om exempelvis $f(x)=\sin{x}$, men inte om $f(x)=2x$. :)

Råkade redigera till sin(x) precis innan du skrev kommentaren, förlåt.

Man använder satsen med det bästa namnet

Smaragdalena skrev:

Man använder satsen med det bästa namnet

Tack så mycket Smaragdalena :D

Aha, ingen fara, blev lite förvirrad där bara! 

Det finns många olika bevis för detta påstående. Ett bevis fås genom att MacLaurinutveckla sin(x) – när x går mot noll blir approximeringen $f(x)=\sin{(x)}\approx x$ riktigt bra (om du är osäker, rita upp funktionerna, så kan du se att funktionernas värden är nästan lika kring x = 0).

Ett annat är att använda enhetscirkeln. Vi ritar upp enhetscirkeln och en punkt $(x,\sin{(x)})$ (för enkelhetens skull är x i radianer, det spelar egentligen ingen roll) på enhetscirkeln (VARNING FÖR FULA ILLUSTRATIONER 😅):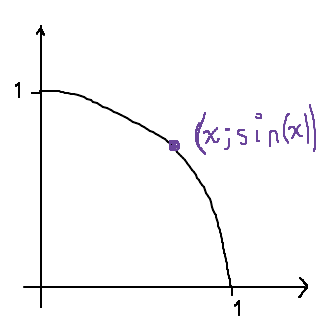

Vi undersöker nu tårtbiten som bildas i samband med denna punkt:

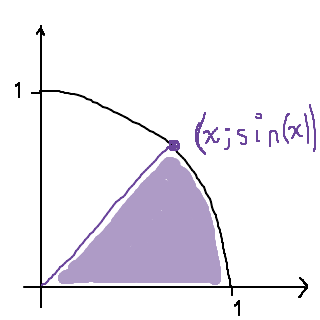
Arean av denna tårtbit kan beräknas som arean av en cirkelsektor. $A_c=\frac{v{r}^2}{2}=\frac{x·1^2}{2}=\frac{x}{2}$

Vi kan approximera denna tårtbit med en triangel:

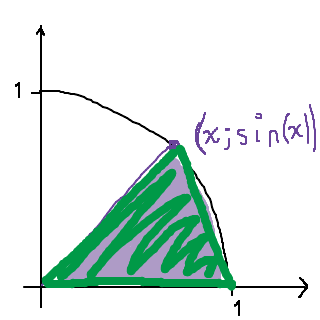
Triangeln har basen 1, och höjden $\sin{(x)}$, och har alltså arean $A_t=\frac{bh}{2}=\frac{1·\sin \left(x\right)}{2}=\frac{\sin \left(x\right)}{2}$. Skillnaden i areorna är den där utbuktningen, längst ut, vid kanten bortom det gröna. :)

Vi har nu två areor, och vi kan undersöka förhållandet mellan dessa. Vad är $\frac{A_t}{A_c}$? Tja, $\frac{A_t}{A_c}=\frac{\left({\displaystyle \frac{\sin \left(x\right)}{2}}\right)}{\left({\displaystyle \frac{x}{2}}\right)}=\frac{\sin \left(x\right)}{x}$. Vad händer då om x närmar sig noll?

Vi undersöker hur det ser ut för några olika stora vinklar x:

Om x är stort: 

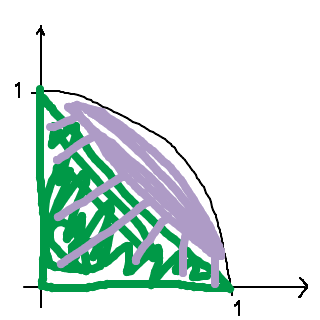
Väldigt stor skillnad. 

Om x är halvstort får vi exemplet med den första bilden. 

Om x är litet:

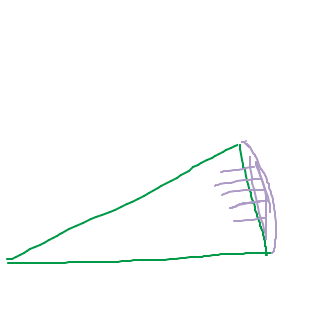
När x går mot noll blir den lila utbuktningen mindre och mindre, och när x är tillräckligt litet är den i princip icke-existerande. Det innebär att areorna är lika stora, och förhållandet mellan dem blir då 1. Alltså, $\underset{x\to 0}{\lim }\left(\frac{\sin \left(x\right)}{x}\right)=1$. (detta bevis bör upprepas för då x går mot noll från vänster, men det är precis samma sak). :)