Hur coroliskraften är riktad och hur bollens bana kommer böjas av (Fysik/Universitet)

När A kastar så är v_rel initialt riktad från A till B. När B kastar så är v_rel initialt riktad från B till A.

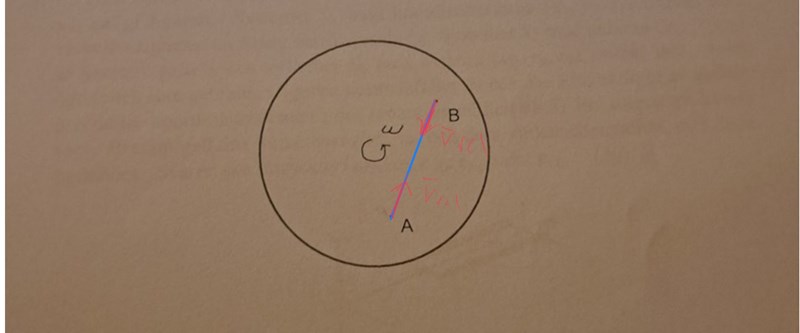
PATENTERAMERA skrev:
När A kastar så är v_rel initialt riktad från A till B. När B kastar så är v_rel initialt riktad från B till A.

Hur vet man att det handlar om ett rörligt koordinatsystem som A och B befinner sig i när de kastar boll till varandra och inte ett oprimmad koordinatsystem? Jag förstår inte varför båda har en v_rel och inte en vanlig v?

Det står att det är ett roterande system i problemtexten. A och B roterar med skivan. Det är ju v_rel som spelar roll för Corioliskraften.

PATENTERAMERA skrev:
Det står att det är ett roterande system i problemtexten. A och B roterar med skivan. Det är ju v_rel som spelar roll för Corioliskraften.

Men jag hade för mig att primmade koordinatsystem var icke roterande system tex om vi talar om masscentrumsystem där axlarna inte roterar till skillnad från oprimmade koordinatsystem där det är roterande system.

Ett system roterar om det roterar. Det påverkas inte av om du sätter prim på koordinaterna eller inte. I de flesta böcker brukar man använda prim på det roterande koordinatsystemet, men det är bara en konvention.

PATENTERAMERA skrev:
Ett system roterar om det roterar. Det påverkas inte av om du sätter prim på koordinaterna eller inte. I de flesta böcker brukar man använda prim på det roterande koordinatsystemet, men det är bara en konvention.

Så det kroppsfixa systemet där kroppen befinner sig i roterar där A och B ligger på ? Men om v_rel är riktad åt det hållet i A och i B som du ritat. Hur är a_rel riktad då?

Ja, det är väl det som man skall klura ut.

PATENTERAMERA skrev:
Ja, det är väl det som man skall klura ut.

Det enda jag lyckades klura ut utifrån din ritning på v_rel i A och B är att F_cor måste vara vinkelrät mot dem och hur den är riktad vet jag inte

Hur ser rörelseekvationerna ut i ett roterande koordinatsystem? Med tröghetskrafter et.c.

PATENTERAMERA skrev:
Hur ser rörelseekvationerna ut i ett roterande koordinatsystem? Med tröghetskrafter et.c.

Hm ingen aning. Såhär säger facit.

1) Jag undrar hur man vet att F_cor i punkten B är riktad åt det hållet som visas i bilden nedan och sen undrar jag samma sak för punkten A. Vad menar de med att man ska bestämma skruvregeln?

2) vi tänkte ju rätt på v_rel i A och B , men förstår inte riktigt de här streckade linjerna som har med B-A och A-B att göra ?

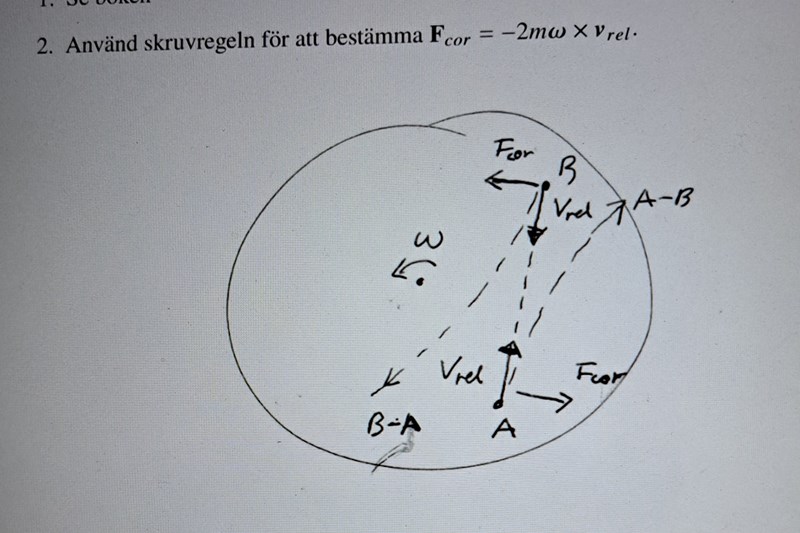
$\vec{ω}$ är vinkelrät mot papprets plan. Dvs rakt mot betraktaren.

Du får ta och räkna ut vilken riktning som vektorn $\vec{ω} \times {\vec{v}}_{r e l}$ har. Corioliskraften är motriktad denna vektor.

De streckade linjerna beskriver lite på en höft hur bollen kommer att röra sig - inte riktigt rakt utan i en krökt bana under påverkan av Corioliskraft (och Centrifugalkraft).

I det roterande systemet så blir rörelseekvationen (med antagande att $\vec{ω}$ är konstant)

$m {\vec{a}}_{r e l} = {\vec{F}}_{Verklig} + {\vec{F}}_{Cor} + {\vec{F}}_{Centrifug}$ .

Om du har svårt att se åt vilket håll bollarna avviker eller hur $\mathbf{F}_{cor}$ pekar med högerregeln kan du sätta in enkla vektorer för $\mathbf{\omega}$ och $\mathbf{v}_{rel}$ och faktiskt räkna ut kryssprodukten. Då får du en riktningsvektor för Corioliskraften. Låt till exempel $\mathbf{\omega}= (0,0,\omega)$

PATENTERAMERA skrev:
$\vec{ω}$ är vinkelrät mot papprets plan. Dvs rakt mot betraktaren.

Du får ta och räkna ut vilken riktning som vektorn $\vec{ω} \times {\vec{v}}_{r e l}$ har. Corioliskraften är motriktad denna vektor.

De streckade linjerna beskriver lite på en höft hur bollen kommer att röra sig - inte riktigt rakt utan i en krökt bana under påverkan av Corioliskraft (och Centrifugalkraft).

I det roterande systemet så blir rörelseekvationen (med antagande att $\vec{ω}$ är konstant)

$m {\vec{a}}_{r e l} = {\vec{F}}_{Verklig} + {\vec{F}}_{Cor} + {\vec{F}}_{Centrifug}$ .

Jag förstår inte vad w×v_rel har för koppling till Fcor? Är inte Fcor=macor? acor=2w×vrel. Hur menar du att jag ska räkna ut vilken riktning den har? Menar du mha högerhandsregeln?

Ja, använd den geometriska definitionen av kryssprodukten med högerhandsregeln.

PATENTERAMERA skrev:
Ja, använd den geometriska definitionen av kryssprodukten med högerhandsregeln.

Det gick tyvärr inte bra när jag gjorde det. Jag placerade bara min höger hand där v_rel i A går till B och sen tummen upp för w så långfingret pekar åt vänster (coroliskraften då?)

Det finns ett minustecken i uttrycket. Hur påverkar det riktningen?

PATENTERAMERA skrev:
Det finns ett minustecken i uttrycket. Hur påverkar det riktningen?

ingen aning varför den dyker upp. Hur ska man använda högerhandsregeln här eller hur är det liksom tänkt?

Om uxv har en viss riktning, vilken riktning har -uxv?

PATENTERAMERA skrev:
Om uxv har en viss riktning, vilken riktning har -uxv?

Motsatt riktning?

Så hur är Corioliskraften riktad?

PATENTERAMERA skrev:
Så hur är Corioliskraften riktad?

Ja det beror på om du syftar på punkt B eller A. I A så är det ju v_rel och i B är det -v_rel

Ta en i taget. Börja med A och ta sedan B.

PATENTERAMERA skrev:
Ta en i taget. Börja med A och ta sedan B.

Ja i A blir Fcor riktad åt vänster om jag har tummen riktad mot mig som är w:s riktning och pekfingret visar riktning från A till B , sen pekar långfingret åt vänster där Fcor är riktad åt. I B så blir Fcor riktad åt höger med samma procedur

Tvärt om blir det väl?

PATENTERAMERA skrev:
Tvärt om blir det väl?

om högerhandsregeln ska ge riktning på Fcor så är det så jag har gjort i #25. Jag vet inte varför riktningen ska vara åt andra hållet..

Du fick kryssprodukten att gå mot vänster tidigare, men eftersom formeln för corioliskraften har ett minustecken i sig så blir kraften till höger. Eller hur?

PATENTERAMERA skrev:
Du fick kryssprodukten att gå mot vänster tidigare, men eftersom formeln för corioliskraften har ett minustecken i sig så blir kraften till höger. Eller hur?

Ja precis i A blir det så medan i B blir det åt vänster.

Ja, som i facit.