2
svar
116
visningar
nilson99 är nöjd med hjälpen
Hur förändrar en konstant en andragradsfunktion?
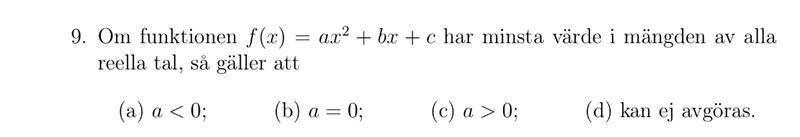 svar c)
svar c)
Förstår varför det inte är b), men hur kommer det sig att vi får minimipunkt när a>0 och att vi får maximipunkt när a<0? Undrar också hur man säkert ska veta att svaret är c) då det kanske hade varit d).
nilson99 skrev:
svar c)
Förstår varför det inte är b), men hur kommer det sig att vi får minimipunkt när a>0 och att vi får maximipunkt när a<0? Undrar också hur man säkert ska veta att svaret är c) då det kanske hade varit d).
Rita (dvs a=1, b=c=0) och (dvs a=-1, b=c=0) så ser du följande:
- Om a > 0 så liknar parabeln en "glad mun" (minnesregel: Positiv = Glad). Parabeln har då en minimipunkt.
- Om a < 0 så liknar parabeln en "ledsen mun" (minnesregel: Negativ = Ledsen). Parabeln har då en maximipunkt.
Med kvadratkomplettering kan funktionen skrivas
- Om så är ett positivt tal varför och olikheten blir en likhet precis då .
- Om så är ett negativt tal varför och olikheten blir en likhet precis då .
- Om så behöver man inte kvadratkomplettera (då skulle man dividerat med noll!) eftersom då är och funktionen saknar minsta värde och saknar största värde (förutsatt att ).


