Hur gör man här?

3175) på denna uppgift, när man ska hitta f(x) = ax^2 + bx + c så tänkte jag att c=0 då detta samband börjar från origo. b = 0 också då origo är minimipunkten och därmed 0 är Xsym. Detta betyder att f(x) = ax^2
För att sedan lösa detta tog jag ett ekvationssystem
25 = 2500a
45 = 4900a
MEn detta går inte ihop. Hur löses detta?
c = 0, det är rätt tänkt.
Det kan verkar rimligt att minimipunkten ligger i origo, men vi vet inte hela kurvan. Modellen gäller bara för x >= 0, så för x < 0 kan vad som helst hända.
Använd ax^2 + bx.
Borde då inte oavsett Xsym vara 0???
Alltså x-värdet för symmetrilinjen?
Hej, skulle upskatta hjälp på denna :)
Nej symmetrilinjen behöver inte ligga på x = 0, i själva verket ligger den på cirka -10
se kurvan nedan
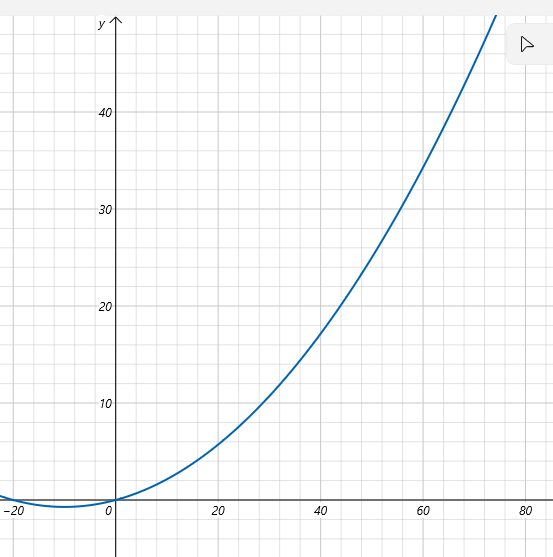
Fär att bestämma a och b i din andragradare sätter du bara in de två kända punkterna och löser ekvationssystemet



