Hur hittar man den övre gränsen för en rekursiv talföljd?
Hej, i problemet ska man göra följande för att få rätt svar:
 Metod:
Metod:
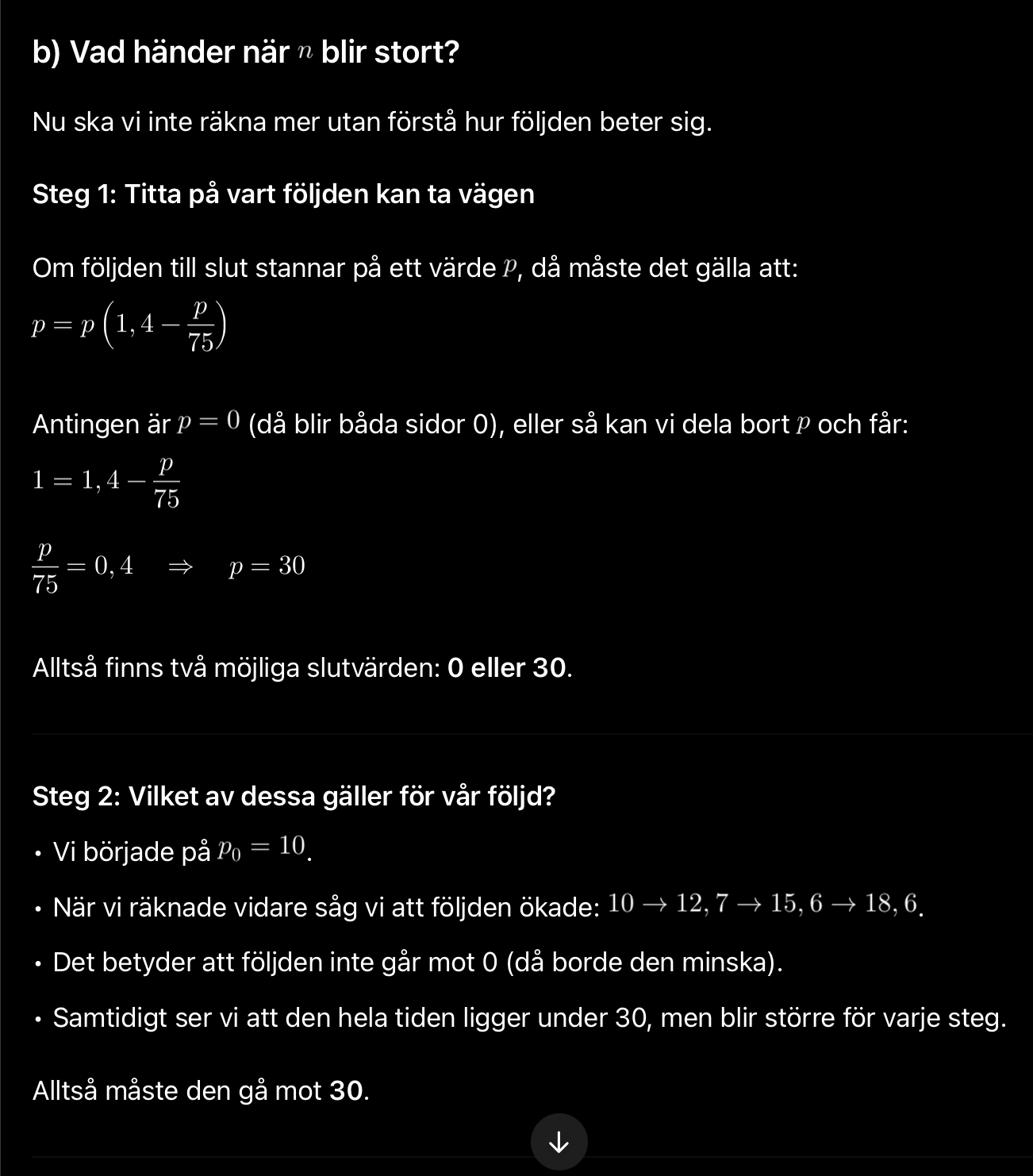
’Jag undrar enbart VARFÖR man gör på följande sätt?
Om man tar 30/75 får man 0.4 så parantesen närmar sig 1 då p går mot trettio, och eftersom den blir så nära ett kommer den aldrig att bli mer än 30. Hoppas detta hjälper.
Säg exempelvis att talföljden kommer över 30 (hypotetiskt) då kommer den multipliceras med en förändringsfaktor mindre än 1 så den kommer minska ner till 30 igen.
Har ni arbetat med gränsvärden i Matematik 5? Och i synnerhet gränsvärden av rekursiva talföljder? Det är nämligen det som GPT håller på med. (Det är väl någon chatbot såsom gpt, eller hur?) Och det var egentligen inte vad som efterfrågas i uppgiften, vill jag tro.
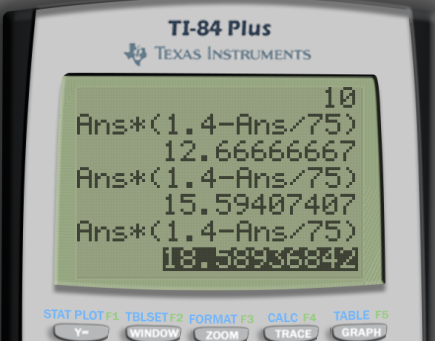
Ta fram en miniräknare och använd formeln från uppgiften ett antal gånger. Frågan i (b) är faktiskt bara en fortsättning på (a), där man fortsätter att beräkna , , o.s.v. När man kommit fram till eller högre, så inser man att värdet stabiliserar sig på ungefär .
Nedan ser du hur man tar fram de tre första värdena på en TI-84 (det funkar likadant på TI-82 stats), d.v.s. lösning till (a)

Nu är det bara att använda samma formel om och om igen.
Ifall du kan programmera lite grann, så är det betydligt snabbare att beräkna värdena på talföljden m.h.a. ett enkelt skript.
Alternativt kan man använda sig av geogebra, där man definierar f(p) = p * (1.4 - p / 75), d.v.s. formeln på högerledet kallas för f(p). Sedan kan talföljden tas fram m.h.a. kommandot Iterationslista(f, 10, 25) som tillämpar formeln f(p) totalt 25 gånger, med startvärdet 10. På så sätt kommer geogebra spotta ut en lista med .
Om du dock vill veta varför man försöker hitta begränsningar för talföljden och vart n och n-1 tagit vägen i uträkningen av GPT, så får du gärna bortse från detta inlägg.
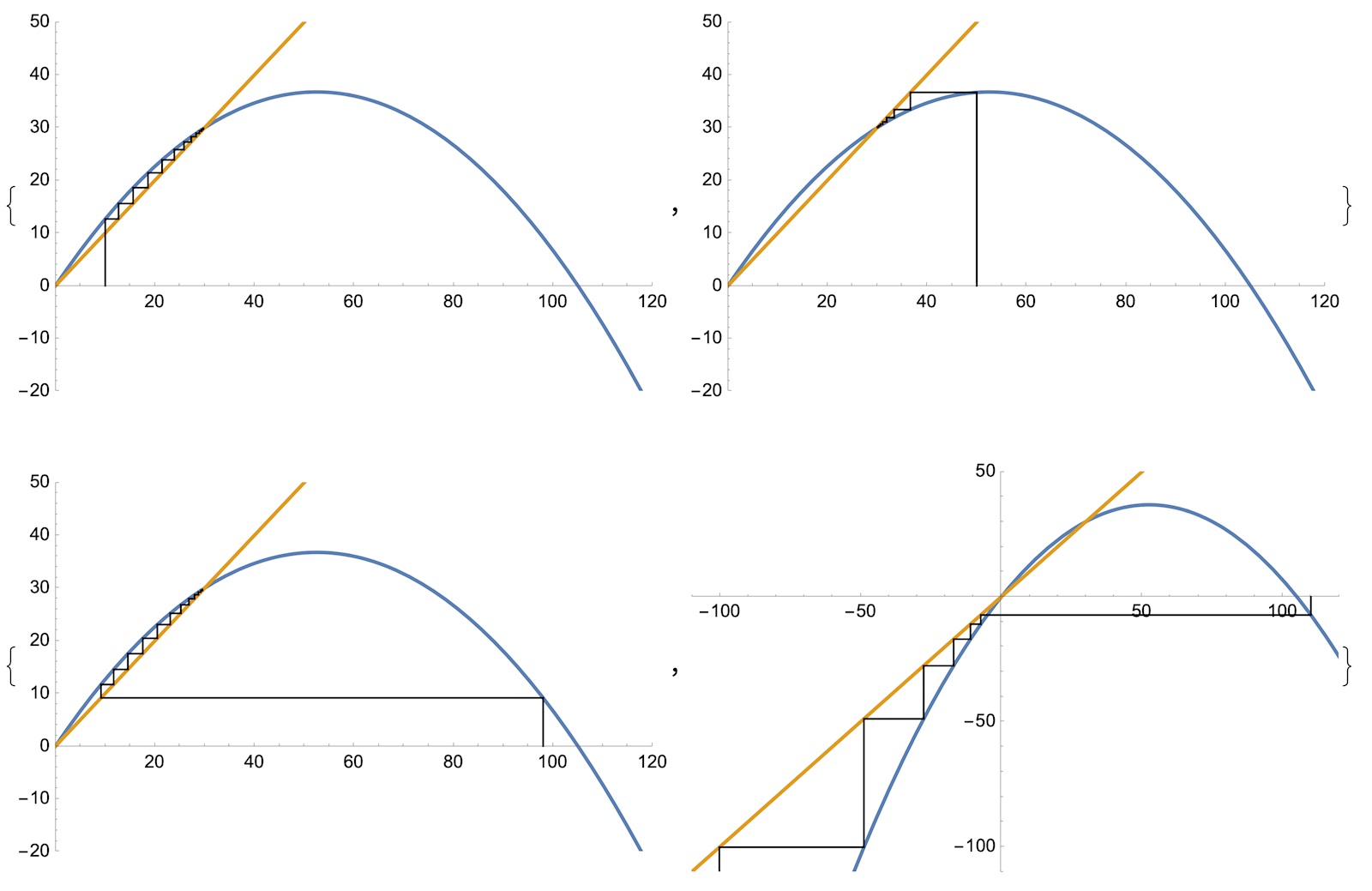
Studera graferna
y=x(1.4-x/75)
y=x
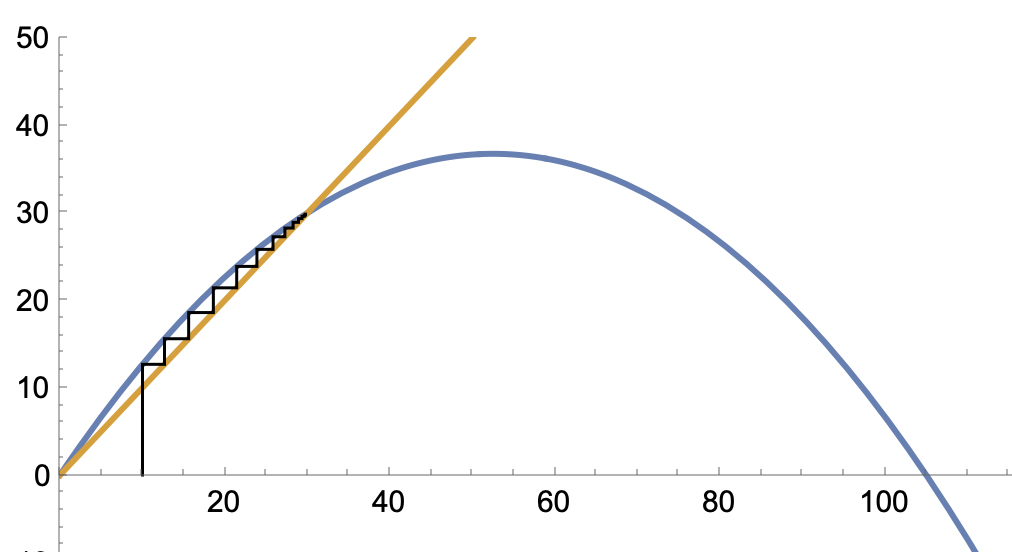
Man ser genom att välja ett lämpligt startvärde på x (dvs. p_0) kommer "rekursionstrappstegen" att konvergera. Om man dock väljer "fel" p_0 (>0) fås en divergens. Kan du lista ut vilket gränsvärde för p_0 där det börjar divergera?
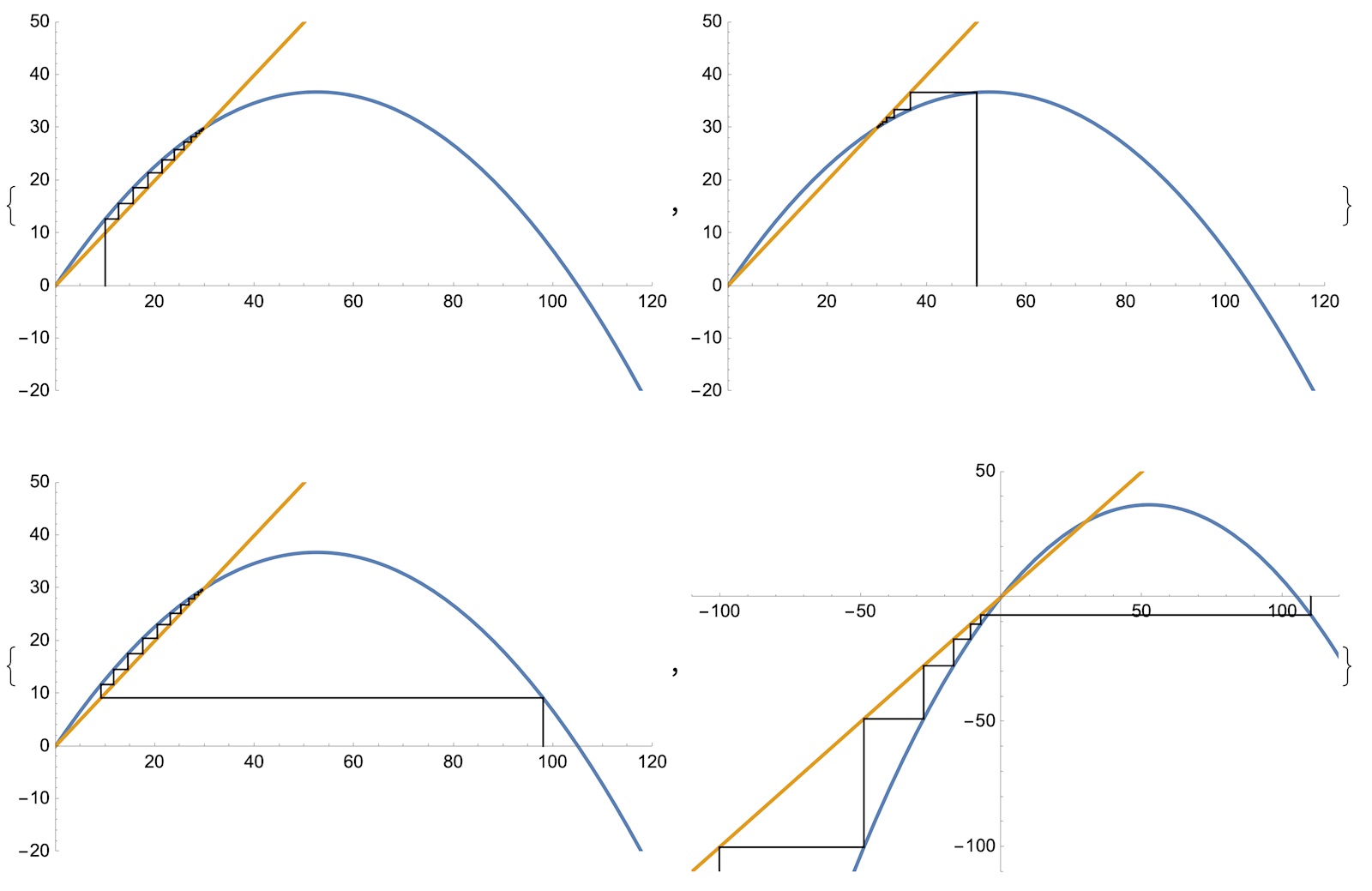
Bild 1: p_0=10
Bild 2: p_0=50
Bild 3: p_0=98
Bild 4: p_0=110
LuMa07 skrev:Har ni arbetat med gränsvärden i Matematik 5? Och i synnerhet gränsvärden av rekursiva talföljder? Det är nämligen det som GPT håller på med. (Det är väl någon chatbot såsom gpt, eller hur?) Och det var egentligen inte vad som efterfrågas i uppgiften, vill jag tro.
Ta fram en miniräknare och använd formeln från uppgiften ett antal gånger. Frågan i (b) är faktiskt bara en fortsättning på (a), där man fortsätter att beräkna , , o.s.v. När man kommit fram till eller högre, så inser man att värdet stabiliserar sig på ungefär .
Nedan ser du hur man tar fram de tre första värdena på en TI-84 (det funkar likadant på TI-82 stats), d.v.s. lösning till (a)
Nu är det bara att använda samma formel om och om igen.
Ifall du kan programmera lite grann, så är det betydligt snabbare att beräkna värdena på talföljden m.h.a. ett enkelt skript.
Alternativt kan man använda sig av geogebra, där man definierar f(p) = p * (1.4 - p / 75), d.v.s. formeln på högerledet kallas för f(p). Sedan kan talföljden tas fram m.h.a. kommandot Iterationslista(f, 10, 25) som tillämpar formeln f(p) totalt 25 gånger, med startvärdet 10. På så sätt kommer geogebra spotta ut en lista med .
Om du dock vill veta varför man försöker hitta begränsningar för talföljden och vart n och n-1 tagit vägen i uträkningen av GPT, så får du gärna bortse från detta inlägg.
Tack för svar! Anledningen till att jag frågar ChatGPT är för att jag vill ha en metod + förklaring till varför man gör just så ifall det skulle dyka upp en liknande fråga på provet. Jag har en casio fix cg 50. Vet du hur man kan göra? Skulle du kunna förklara ChatGPT metoden?
Trinity2 skrev:Studera graferna
y=x(1.4-x/75)
y=x
Man ser genom att välja ett lämpligt startvärde på x (dvs. p_0) kommer "rekursionstrappstegen" att konvergera. Om man dock väljer "fel" p_0 (>0) fås en divergens. Kan du lista ut vilket gränsvärde för p_0 där det börjar divergera?
Bild 1: p_0=10
Bild 2: p_0=50
Bild 3: p_0=98
Bild 4: p_0=110
Jag förstår inte riktigt vad du har gjort. Vad innebär konvergera?
Konvergera = går mot/närmar sig
Divergera = avviker ifrån
Om vi har p0=10 så blir p1=12.6667 och vi går horisontellt ut mot linjen y=x, och sedan rakt upp mot grafen för att finna p2=15.5941, och sedan ut mot y=x för att finna p3=18.5894 osv.
Man "trappstegar sig fram" på detta sättet och du ser att trappstegen trycks ihop mellan den gula och den blå grafen. Den konvergerar mot 30.
Genom att välja andra startvärden p0 fås andra "trappor" (se ovan) och den del divergerar, som i den 4:e bilden.
Anonym_15 skrev:Jag har en casio fix cg 50. Vet du hur man kan göra?
I huvudmenyn väljer du 8: Recursion

Det borde stå på första raden. Om inte, så tryck F3 för att ändra typ och sedan F2 för att välja . Tryck på kursortangenten till höger för att börja skriva rekursiv formel och mata in formeln och bekräfta formeln med knappen EXE.

Tryck nu på F5 för att ställa in rekursionen. Start = första n-värde, End=sista n-värde som beräknas, (begynnelsevillkoret). Bekräfta inställningarna m.h.a. knappen EXE
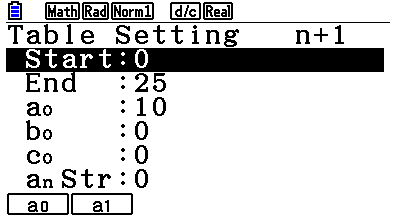
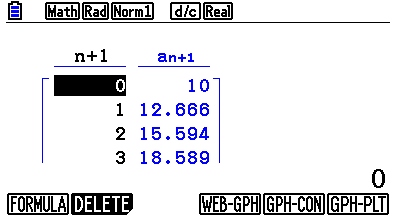
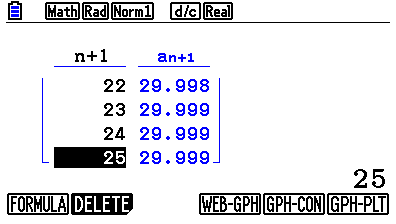
Tryck på F6 och miniräknaren kommer att beräkna ett antal element i den rekursiva talföljden:
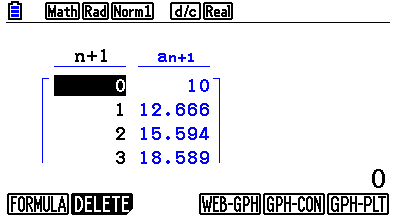
Skrolla ner för att komma åt värden för stora

Det ChatGPT (eller vem som nu har skrivit det där) menar, är att för väldigt stora n t.ex n=1000001 gäller att
Vilket "i princip" innebär att
eftersom närliggande tal i talföljden för stora n är väldigt lika. Därifrån härleds att gränsvärdet måste vara 0 eller 30.
LuMa07 skrev:Anonym_15 skrev:Jag har en casio fix cg 50. Vet du hur man kan göra?
I huvudmenyn väljer du 8: Recursion
Det borde stå på första raden. Om inte, så tryck F3 för att ändra typ och sedan F2 för att välja . Tryck på kursortangenten till höger för att börja skriva rekursiv formel och mata in formeln och bekräfta formeln med knappen EXE.
Tryck nu på F5 för att ställa in rekursionen. Start = första n-värde, End=sista n-värde som beräknas, (begynnelsevillkoret). Bekräfta inställningarna m.h.a. knappen EXE
Tryck på F6 och miniräknaren kommer att beräkna ett antal element i den rekursiva talföljden:
Skrolla ner för att komma åt värden för stora
Stort tack för att du tar dig tiden att skriva detta, det var till stor hjälp! Ha en sista fråga: är det alltid så att man kan bevisa att en rekursiv talföljd har ett gränsvärde genom att sätta p n+1 = pn?
Om man redan vet att gränsvärdet existerar, så kan man klura ut vad gränsvärdet blir genom att skicka i rekursionssambandet. Tanken är att både och går mot samma tal då och detta tal betecknas med , vilket nämndes av (bl.a.) Peter i #10.
Problemet är att denna metod funkar för att hitta ett gränsvärde förutsatt att man i förväg motiverat att gränsvärdet finns. Följande exempel visar att denna metod kan få en tro att gränsvärdet finns trots att det inte gör det. Att visa att ett gränsvärde av en rekursiv talföljd existerar är i allmänhet en väldigt svår fråga.
Exempel:
Låt med begynnelsevillkoret . Antag att betecknar gränsvärdet av talföljden . När man gör gränsvärdesövergång i rekursionssambandet, så får man att .
Slutsats: Talföljden har gränsvärdet .
En sådan slutsats är dock felaktig! Tittar man på talföljdens element, så får man:
, , , , , o.s.v.
Värdena alltså alternerar mellan 0 och 2 och de närmar sig verkligen inte talet 1. Problemet i denna lösning är att man inte visat att gränsvärdet faktiskt existerar (vilket det inte gör).
Tillbaka till uppgift 1435 från Matematik 5000+ kurs 5: (Texten nedan innefattar färdigheter på en högre nivå än Matematik 5)
Genom att lösa ekvationen får man reda på att gränsvärdet måste vara 0 eller 30 förutsatt att gränsvärdet existerar. Det återstår dock att visa att gränsvärdet faktiskt existerar.
I rekursionssambandet kan man undersöka högerledet. Det är ett andragradspolynom i variabeln vars största värde är 36.75. Det innebär att högerledet aldrig kommer att överstiga talet 36.75.
Om man nu undersöker innehållet av parentesen , så ser man att parentesens värde är
- större än då
- lika med då
- mindre än då .
Eftersom rekursiva formeln är skriven på formen , så innebär detta att talföljden är växande så länge värdena inte överstigit och den är avtagande ifall värdet överstigit .
Begynnelsevillkoret är , så talföljden kommer att växa. Frågan är om värdena kommer att överstiga 30 eller inte. Genom att kolla på grafen av parabeln (d.v.s. hela högerledet i rekursionsformeln), så ser man att ifall .
Vad har man visat då? Talföljden med begynnelsevillkoret är växande och uppåt begränsad av värdet . Det finns en sats som säger att monotona (t.ex. växande) begränsade talföljder har ett gränsvärde. Därmed har man motiverat att gränsvärdet existerar och således är det lagligt att göra gränsvärdesövergång och i rekursionsformeln då .