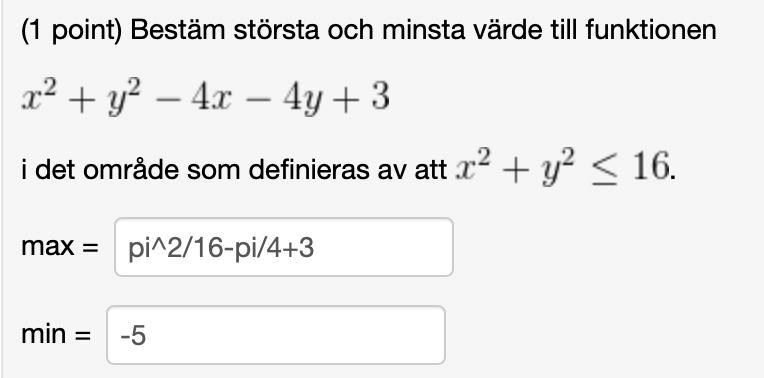
Hur hittar man maximat till en flervariabelfunktion?

Om du bryter ut $r^2$ kan du använda trigettan för att förenkla lite. Om man också bryter ut -4r får man

$r^2 -4r(\cos(v)+\sin(v))+3$

Undersök sen vad v borde vara för att maximera detta uttryck.

x² + y² - 4x - 4y + 3 = (x - 2)² + (y -2)² - 5 = ${\left|\left|\left(x,y\right)-\left(2,2\right)\right|\right|}^2$ - 5

Från detta ser vi att minvärdet/maxvärden antas då avståndet mellan (x,y) och (2,2) är minst/störst.

Rita figur.

min = -5, då (x,y) = (2,2)

max = 16$\sqrt{2}$ + 19, då (x,y) = (-2$\sqrt{2}$, -2$\sqrt{2}$).

Du kan även söka möjliga max/min punkter i det inre av området genom att hitta punkter som uppfyller

$\nabla f=0$.

På randen kan du hitta möjliga max/min punkter genom att använda Lagrange-multiplikator-metoden.

Sätt L(x, y, $\lambda$) = f(x, y) + $\lambda$(x² + y² - 16) och finn punkter som uppfyller systemet

$\frac{\partial L}{\partial x}$ = 0

$\frac{\partial L}{\partial y}$ = 0

$\frac{\partial L}{\partial \lambda }$ = 0.