Hur högt når kroppen (spännkrafter)

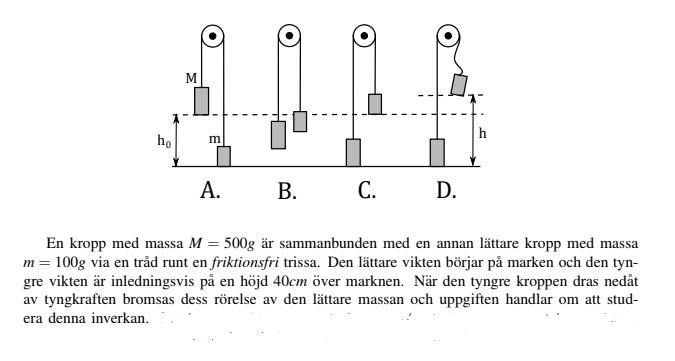
Jag har inget facit på fördjupningsproblem 1 och skulle därför fråga vad ni resonerar er fram till. Jag tänker att det finns en maximal höjd som en väldigt lätt vikt kan få eftersom att tråden har en begränsad längd och eftersom den mekaniska energin är bevarad kommer ingen extra energi tillkomma när den tunga massan slår i golvet. Eftersom den lätta massan inte heller kan "dra" upp den tunga massan med tillräcklig kraft så kommer den lätta massan nå en maximal höjd som är lika med trådens längd i vertikal riktning. Om man beräknar detta algebraiskt med rörelseenergi och potentiell energi kan man säkert få en höjd som blir ofantligt stor om man gör den lätta massan ofantligt liten, men det är ju för att man ej tar hänsyn till trådens längd och spännkraft. I verkligheten kommer tråden begränsa den lätta viktens maximala höjd.

Jag undrar om detta är ett korrekt resonemang eller hur skulle ni svara på en sådan fråga?

Om den stora massan faller fritt, dvs den lilla massan är så liten så den nästan inte påverkar accerationen får systemet en hastighet som motsvaras av Mgh = Mv^2/2 större hastighet än så kommer systemet aldrig att få.

Samma hastighet kommer den lilla massan att ha när den stora slår i golvet. Maxhöjden på den lilla bestäms sen av de vanliga rörelselagarna eller med energiprincipen.

Den lilla kroppens hastighet när den stora slår i backen är alltså $\sqrt{2 g h}$ , den befinner sig då på höjden h, hur mycket högre kan den maximalt komma därifrån?

Ture skrev:
Om den stora massan faller fritt, dvs den lilla massan är så liten så den nästan inte påverkar accerationen får systemet en hastighet som motsvaras av Mgh = Mv^2/2 större hastighet än så kommer systemet aldrig att få.
Samma hastighet kommer den lilla massan att ha när den stora slår i golvet. Maxhöjden på den lilla bestäms sen av de vanliga rörelselagarna eller med energiprincipen.
Den lilla kroppens hastighet när den stora slår i backen är alltså $\sqrt{2 g h}$ , den befinner sig då på höjden h, hur mycket högre kan den maximalt komma därifrån?

Tack Ture för svar. Eftersom hastigheten är samma så kommer den ha en hastighet om cirka 2,29 m/s på höjden h. t = (v - v0) / a = 0-229 / -9.82 = 0,2332 s. När tråden slaknar kommer tyngdaccelerationen verka i motsatt riktning mot viktens färdriktning.

s = v0t + (at^2) / 2 = 2,29 * 0,2332 + (-9.82 * 0,2332^2) / 2 = 0,27 m

Alltså är den maximala höjden h + h0 = 0,27 + 0,4 = 0,67 m? Stämmer detta eller vad har jag missat?

Om den lilla massan är lätt kommer den stora massan slå i golvet (från höjden $h_0=0.4\mathrm{m}$ ) med hastigheten 2.8m/s eftersom

$Mgh_0=\frac{Mv^2}{2} \, \Rightarrow v^2=2gh_0$

När den stora massan rört sig sträckan $h_0$ måste också den lilla massan ha rört sig sträckan $h_0$ .

Alltså befinner sig den lilla massan på höjden $h_0$ med hastigheten $v$ . Sedan fortsätter den lilla massan av bara farten upp till höjden $h_1$ .

En energibetraktelse ger

$\frac{mv^2}{2}+mgh_0=mgh_1$

$\frac{m(2gh_0)}{2}+mgh_0=mgh_1$

$h_1=2h_0$

Jroth skrev:
Om den lilla massan är lätt kommer den stora massan slå i golvet (från höjden $h_0=0.4\mathrm{m}$ ) med hastigheten 2.8m/s eftersom
$Mgh_0=\frac{Mv^2}{2} \, \Rightarrow v^2=2gh_0$
När den stora massan rört sig sträckan $h_0$ måste också den lilla massan ha rört sig sträckan $h_0$ .
Alltså befinner sig den lilla massan på höjden $h_0$ med hastigheten $v$ . Sedan fortsätter den lilla massan av bara farten upp till höjden $h_1$ .
En energibetraktelse ger
$\frac{mv^2}{2}+mgh_0=mgh_1$
$\frac{m(2gh_0)}{2}+mgh_0=mgh_1$
$h_1=2h_0$

Tack så mycket Jroth för en väldigt bra förklaring!

Svara Avbryt

Visa senaste svar