Hur integrerar man e^(-e^x)?

Notera att det inte är $\exp(-e^x)$ som ska integreras. Det finns en till faktor i integralen som möjliggör variabelbyte.

$e^{-x} y^\prime - y = 1 \iff$

$y^\prime - e^x\,y = e^x$,

vilket ger $IF = \exp(-e^x)$. Hela diff:ekvationen multipliceras med IF:

$\exp(-e^x) y^\prime - \exp(-e^x) e^x\,y = \exp(-e^x) e^x \iff$

$( \exp(-e^x)\,y)^\prime = \exp(-e^x) e^x$.

Nu behöver man alltså bestämma $\displaystyle \int \exp\left(-e^x\right) \,e^x\,dx$. Variabelbyte $t = e^x$ med $dt = e^x\,dx$ funkar bra.

Alternativt kan du slippa integrerande faktor helt och hållet och lösa detta som en separabel diff:ekvation.

LuMa07 skrev:

Notera att det inte är $\exp(-e^x)$ som ska integreras. Det finns en till faktor i integralen som möjliggör variabelbyte.

$e^{-x} y^\prime - y = 1 \iff$

$y^\prime - e^x\,y = e^x$,

vilket ger $IF = \exp(-e^x)$. Hela diff:ekvationen multipliceras med IF:

$\exp(-e^x) y^\prime - \exp(-e^x) e^x\,y = \exp(-e^x) e^x \iff$

$( \exp(-e^x)\,y)^\prime = \exp(-e^x) e^x$.

Nu behöver man alltså bestämma $\displaystyle \int \exp\left(-e^x\right) \,e^x\,dx$. Variabelbyte $t = e^x$ med $dt = e^x\,dx$ funkar bra.

---

Alternativt kan du slippa integrerande faktor helt och hållet och lösa detta som en separabel diff:ekvation.

Variabelbyte vid integrering, den var ny. Kan jag bara göra om dx till dt då hehe? Okej men jag tror jag gjorde på ditt sätt och nu fick jag att y = 1 + Ce^t. Men Houston we have a problem. Frågan vill också att den ska vara definierad för intervallet [0, inf) för alla x>0. Så nu återsubstituerar jag in e^x och så får jag att y=1-e^{(e^x)-1}. Btw jag har inte facit men kan det stämma i så fall?

Edit: jag substituerade med vad mitt y blev och det blev inte HL i original ekvationen. Jag måste alltså ha gjorde vid integrering av t*e^-t. VÄNTA, var fick du dt=e^x dx från? Jag fick istället att y=e^{(e^x)-1}-1 men jag får inte heller att detta riktigt stämmer

Sykey skrev:

LuMa07 skrev:

Notera att det inte är $\exp(-e^x)$ som ska integreras. Det finns en till faktor i integralen som möjliggör variabelbyte.

$e^{-x} y^\prime - y = 1 \iff$

$y^\prime - e^x\,y = e^x$,

vilket ger $IF = \exp(-e^x)$. Hela diff:ekvationen multipliceras med IF:

$\exp(-e^x) y^\prime - \exp(-e^x) e^x\,y = \exp(-e^x) e^x \iff$

$( \exp(-e^x)\,y)^\prime = \exp(-e^x) e^x$.

Nu behöver man alltså bestämma $\displaystyle \int \exp\left(-e^x\right) \,e^x\,dx$. Variabelbyte $t = e^x$ med $dt = e^x\,dx$ funkar bra.

---

Alternativt kan du slippa integrerande faktor helt och hållet och lösa detta som en separabel diff:ekvation.

Variabelbyte vid integrering, den var ny. Kan jag bara göra om dx till dt då hehe? Okej men jag tror jag gjorde på ditt sätt och nu fick jag att y = 1 + Ce^t. Men Houston we have a problem. Frågan vill också att den ska vara definierad för intervallet [0, inf) för alla x>0. Så nu återsubstituerar jag in e^x och så får jag att y=1-e^{(e^x)-1}. Btw jag har inte facit men kan det stämma i så fall?

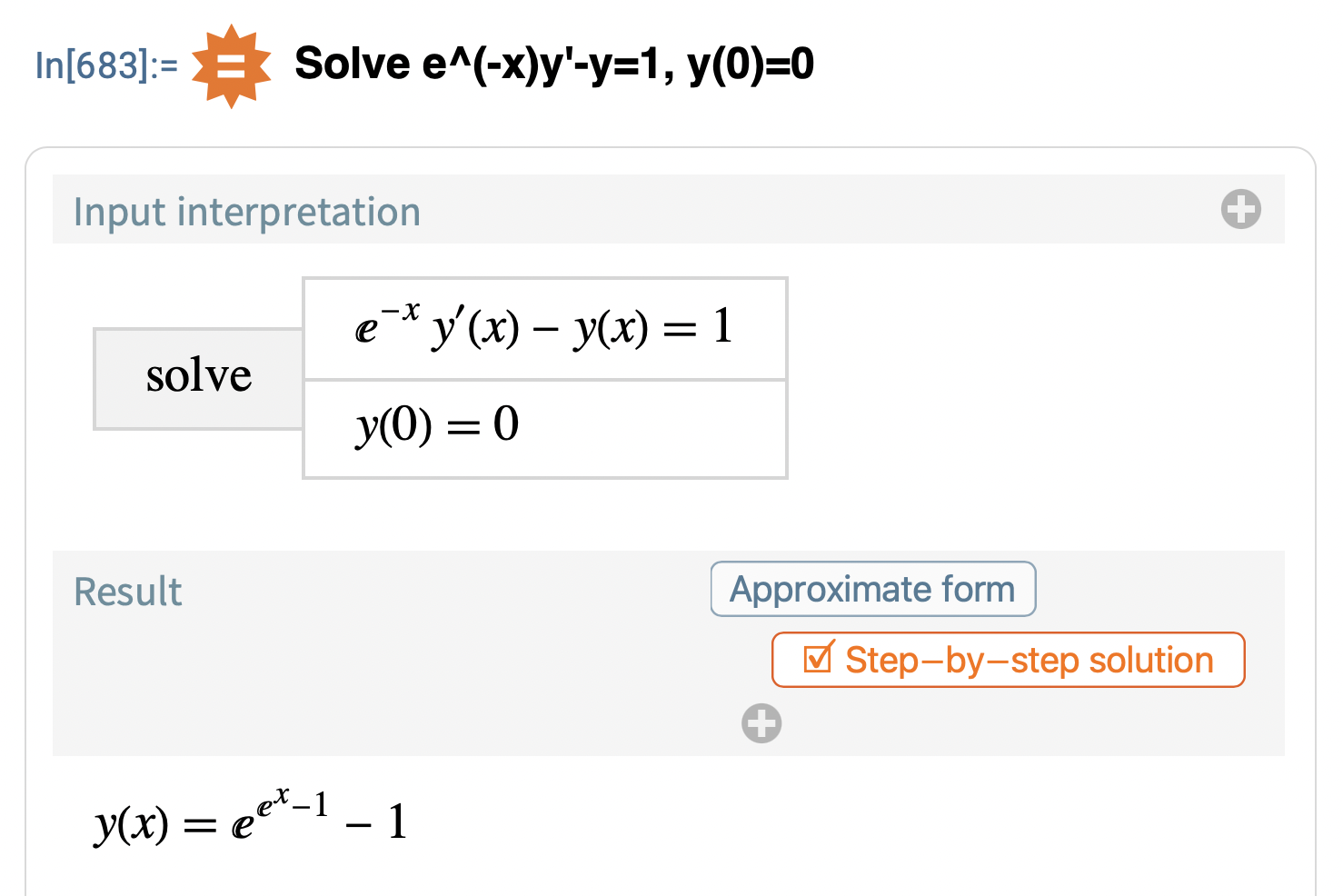
MMA ger

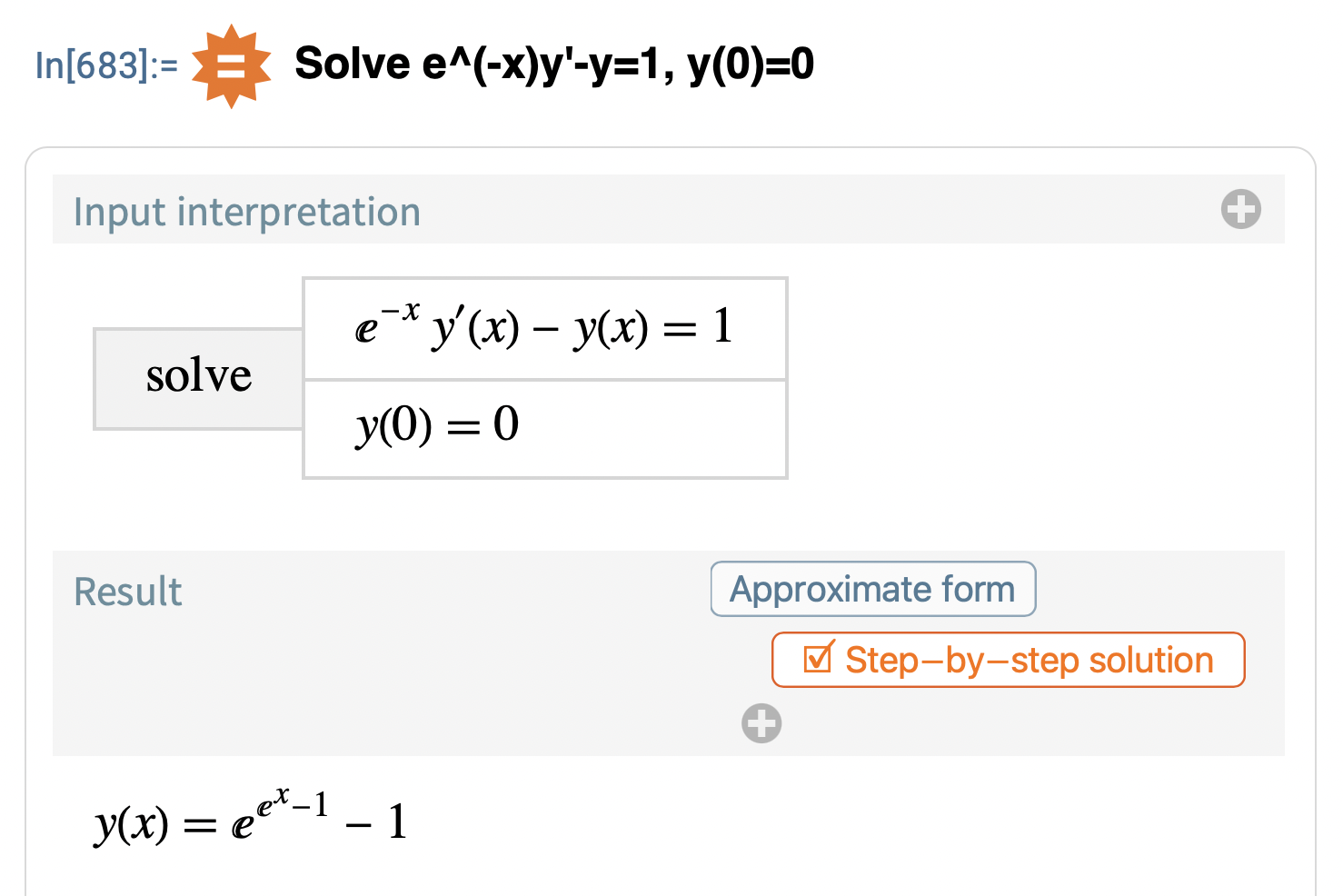
Trinity2 skrev:

Sykey skrev:

Visa föregående citat

LuMa07 skrev:

Notera att det inte är $\exp(-e^x)$ som ska integreras. Det finns en till faktor i integralen som möjliggör variabelbyte.

$e^{-x} y^\prime - y = 1 \iff$

$y^\prime - e^x\,y = e^x$,

vilket ger $IF = \exp(-e^x)$. Hela diff:ekvationen multipliceras med IF:

$\exp(-e^x) y^\prime - \exp(-e^x) e^x\,y = \exp(-e^x) e^x \iff$

$( \exp(-e^x)\,y)^\prime = \exp(-e^x) e^x$.

Nu behöver man alltså bestämma $\displaystyle \int \exp\left(-e^x\right) \,e^x\,dx$. Variabelbyte $t = e^x$ med $dt = e^x\,dx$ funkar bra.

---

Alternativt kan du slippa integrerande faktor helt och hållet och lösa detta som en separabel diff:ekvation.

Variabelbyte vid integrering, den var ny. Kan jag bara göra om dx till dt då hehe? Okej men jag tror jag gjorde på ditt sätt och nu fick jag att y = 1 + Ce^t. Men Houston we have a problem. Frågan vill också att den ska vara definierad för intervallet [0, inf) för alla x>0. Så nu återsubstituerar jag in e^x och så får jag att y=1-e^{(e^x)-1}. Btw jag har inte facit men kan det stämma i så fall?

MMA ger

Okej vet du vad då fick jag rätt svar :DDDDDDDDDDDDDDD. Men när jag kontroll räknade och substituerade e^x=t eftersom det är lättare att jobba med fick jag t^-1(e^t-1)=e^t-1. Men aja rätt är rätt :D:D:DD:D

Tillägg: 9 nov 2025 14:48

Okej nu bliv det rätt y'(x)= e^xe^{e^x}e^-1 sen när vi lägger in det i original funktionen så blir det rätt. Jag hade deriverat fel