Hur kan man visa ?
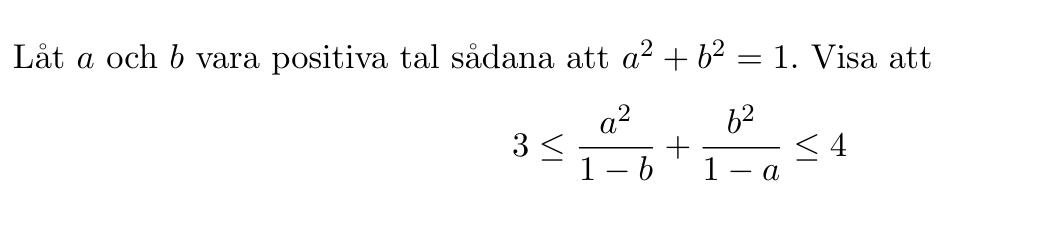
skulle man kunna tänka så här
a2+b2=1↔(a+b)2-2ab=1⇔(a+b)2 =1+2ab
Ja, det där kommer till användning.
Se om du kan förenkla
a2/(1 - b) + b2/(1 - a)
Jag vet inte hur jag kommer vidare därifrån ?
Tänk på att här gäller t.ex
a2 = 1 - b2 = (1 - b)(1 + b)
Du kan då smidigt bli av med bråken.
Dr. G skrev:Tänk på att här gäller t.ex
a2 = 1 - b2 = (1 - b)(1 + b)
Du kan då smidigt bli av med bråken.
Hur vet vi att a2=1-b2
?
Det var givet i uppgiften,
a2+b2 = 1 => ( subtrahera b2 i bägge led )
a2 = 1 -b2
just det
Det här är min fundering
Titta på vad som händer 2 rader från slutet.
a2/(1 - b) + b2/(1 - a) = ... = (1 + b) + (1 + a)
Huh. ?
Dr G jag är förvirrad kan du markera
Du får det till
(1 + b)(1 + a)
men det är plus mellan termerna
(1 + b) + (1 + a)
Tackar det var ett slarvfel
Men jag förstår fortfarande inte hur man kan förenkla (1+a)+(1+b)
Vi vet ju inte varken vad a eller b är .
Du vet att
a2 + b2 = 1, vilket ger att
a2/(1 - b) + b2/(1 - a) = 2 + a + b
(förutsatt att vi inte delar med 0, så a ≠ 1, b ≠ 1)
Du behöver då visa att
3≤2+a+b≤4
när a2 + b2 = 1.
Man bör nog förtydliga att a,b>0. Annars blir det svårt.
Kan någon skicka facit eller lösning?
Suck skrev:Kan någon skicka facit eller lösning?
Jag började räkna på den och såg att uppskattningarna är lite väl grova. Det är sträng olikhet som gäller, uttrycket kan ej anta värdena 3 eller 4.

Här är lösningen från HMT:s hemsida:




