Hur länge dröjer det tills bakteriemängden...

Natascha skrev:

Hej! 

Jag har min sista problemlösning och har fastnat på sista delfrågan. Den lyder såhär: 

Antalet bakterier i en bakteriekultur växer exponentiellt så att det efter en timme finns 2000 bakterier och att det efter ytterligare 5 timmar finns 7000 bakterier i bakteriekulturen. 

Hur länge dröjer det tills bakteriemängden som fanns vid sju timmar har fördubblats? 

Jag har min exponentialfunktion: Y=1600 * 1,28^x 

Jag förstår inte hur jag ska teckna en exponentialfunktion som beskriver som står i frågeställningen. 

Möjligtvis såhär: 2(7000 * 1,28) = 1600 * 1,28^x 

EDIT -nu förstår jag hur du tänkte.

Ja det ser rätt ut OM de efterfrågar tidpunkten då mängden är dubbelt så stor.

Men frågan kan även tolkas som "hur lång tid tar det att fördubbla mängden som fanns vid 7 timmar".

Vad blir svaret i så fall?

Hej Yngve. 

Vad kul att jag i alla fall kom på rätt spår gällande frågan. De efterfrågar precis det du skrev ”Hur lång tid tar det att fördubbla mängden som fanns vid sju timmar”. 

Gäller då fortfarande: 2(7000 * 1,28) = 1600 * 1,28^t 

Jag förstår inte hur faktorn 1,28 har hamnat i vänsterledet. Om det är dubbelt så många bakterier som det fanns vid 7 timmar är det 14 000 bakterier.

Jag har försökt på det sättet med men kommer ej fram fill korrekt svar. 

Blir det: 

14000 = 1600 * 1,28^t? 

Jag dividerar 1600 från HL och får: 

8,75 = 1,28^t 

Stämmer detta? Om ja, hur går jag vidare för att lösa ut t? Med logaritmer? 

Natascha skrev:

Jag har försökt på det sättet med men kommer ej fram fill korrekt svar. 

Blir det: 

14000 = 1600 * 1,28^t? 

Jag dividerar 1600 från HL och får: 

8,75 = 1,28^t 

Stämmer detta? Om ja, hur går jag vidare för att lösa ut t? Med logaritmer? 

Jag skulle ha gjort så här:

Efter 7 timmar var antalet bakterier $y(7)=1600\cdot 1.28^7$.

Efter x timmar var antalet bakterier $y(x)=1600\cdot 1.28^x$.

Vi undrar nu vilket värde på $x$ som gör att detta antal är dubbelt så stort som antalet efter 7 timmar.

Dvs vi ska lösa ekvationen $y(x)=2\cdot y(7)$.

Detta är samma sak som att lösa ekvationen

$1600\cdot 1.28^x=2\cdot 1600\cdot 1.28^7$

$1.28^x=2\cdot 1.28^7$

Kommer du vidare nu?

Ja, med logaritmer. Vet du hur du skall göra det?

Den där faktorn 1,28 skall vara med i vänsterledet, det är jag som inte läser uppgiften ordentligt.

Jag ska både gå Yngves väg till att komma fram till lösningen. Jag ska däremot först försöka lösa: 

8,75 = 1,28^t med logaritmer för att det har vi lärt oss! 😊

Natascha skrev:

...

Blir det: 

14000 = 1600 * 1,28^t? 

...

Stämmer detta?

...

Nej det stämmer inte.

Det är inte 7 000 bakterier efter 7 timmar, det är 7 000 bakterier efter 6 timmar.

Så antalet 14 000 är inte relevant här.

Ahaa! Jag löste precis 8,75 = 1,28^t med logaritmer men det gav mig fel värde. Jag ska försöka med din metod Yngve! Återkommer med lösning! 

Jag försöker lösa: 1,28^x = 2*1,28^7 men jag tappar bort mig lite när det finns något i exponenten i båda led. Ska jag använda logaritmer Yngve? 

 Logaritmlag: lgA^p = p*lg*A 

Är det den jag ska lösa ekvationen med? 

Jag försöker lösa: 1,28^x = 2*1,28^7

Varifrån har du fått den ekvationen? Den saknar lösning (om man förenklar den får man att 1=2).

EDIT: Varifrån kom den där 7:an som exponent i HL? Jag kunde svära på att det var ett x på varje sdia förra gången jag tittade på ekvationen!

Gå igenom Yngves inlägg. Jag försökte först följa din metod men sen hängde sig något där och då hoppade jag över till Yngves. Hur blir det då Smaragdalena? 🤭

Yngve skrev:

Jag skulle ha gjort så här:

Efter 7 timmar var antalet bakterier $y(7)=1600\cdot 1.28^7$.

Efter x timmar var antalet bakterier $y(x)=1600\cdot 1.28^x$.

Vi undrar nu vilket värde på $x$ som gör att detta antal är dubbelt så stort som antalet efter 7 timmar.

Dvs vi ska lösa ekvationen $y(x)=2\cdot y(7)$.

Detta är samma sak som att lösa ekvationen

$1600\cdot 1.28^x=2\cdot 1600\cdot 1.28^7$

$1.28^x=2\cdot 1.28^7$

Kommer du vidare nu

Fortsätt härifrån.

Det var den ekvationen jag nämnde innan. Jag vet inte hur jag ska angripa ekvationen: 

1,28^x = 2*1,28^7 

Ska jag använda logaritmlagen: lgA^p = p * lg A? 

Natascha skrev:

Det var den ekvationen jag nämnde innan. Jag vet inte hur jag ska angripa ekvationen: 

1,28^x = 2*1,28^7 

Ska jag använda logaritmlagen: lgA^p = p * lg A? 

Ja.

Börja med att logaritmera bägge led.

Använd sedan den logaritmlagen på vänsterledet så får du "loss" x.

Tänk på att högerledets 2*1.28^7 är ett vanligt tal, så du behöver inte krångla runt med det uttrycket utan använd istället räknaren direkt där.

Det är något som inte går ihop... 🤔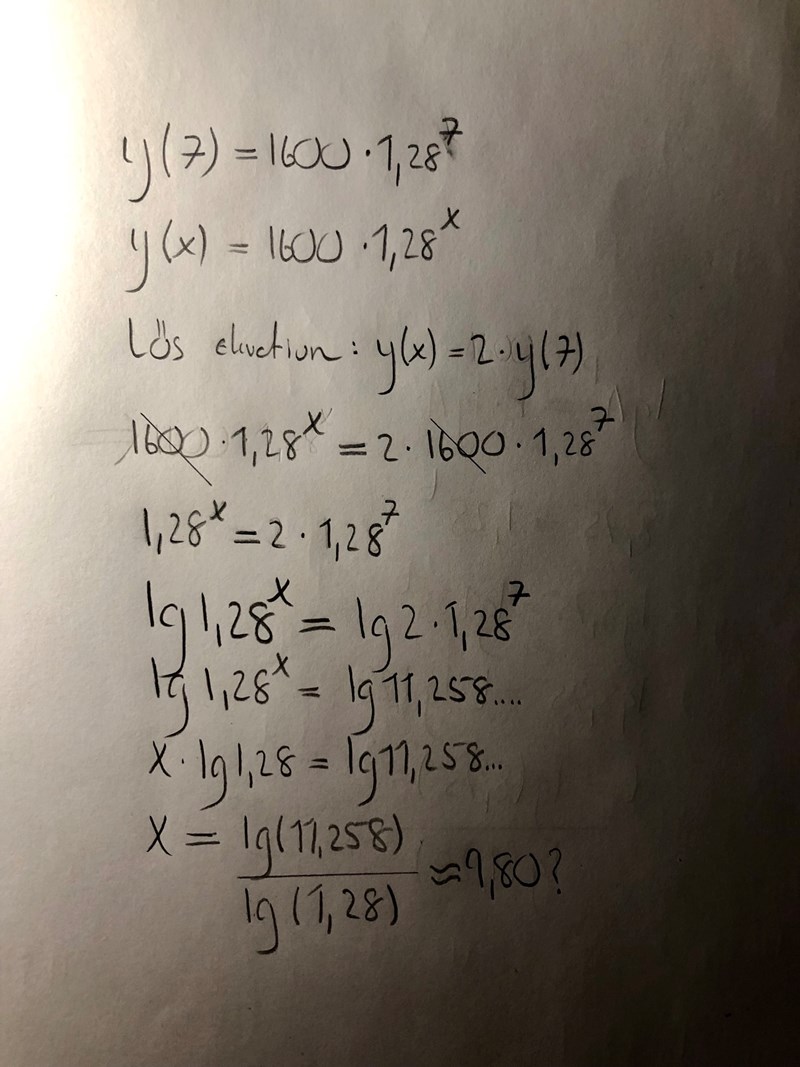

Natascha skrev:

Det är något som inte går ihop... 🤔

Vad menar du inte går ihop? Det ser bra ut tycker jag.

Det enda jag kan invända är

• Avrundningen på rad 7. Den ska vara $2\cdot 1.28^7\approx 11.259$.
• Antal värdesiffror i svaret. Det bör vara $x\approx 9.8$.
• Tolkning av svaret. Uttryck svaret i normalt språk.

Hej!

Vid tidpunkten $x$ timmar finns det $Y(x)$ stycken bakterier i kulturen. Du vill finna $x$ så att

    $Y(x) = 2 \cdot Y(7)$

vilket är samma sak som att finna $x$ så att

    $\log Y(x) = \log 2 + \log Y(7).$ (Förstår du varför det är så?)

Du vet att $Y(x) = 1600\cdot 1.28^{x}$ vilket betyder att dess logaritm är sådan att

    $\log Y(x)=\log1600+\log 1.28^{x}=\log1600+x\cdot\log1.28$;

detta gäller för alla slags tidpunkter $x$, speciellt gäller det för tidpunkten $7$.

    $\log Y(x) = \log 2 + \log Y(7) \iff \log 1600 + x\cdot \log 1.28 = \log 2 + \log 1600 + 7 \cdot \log 1.28.$

Subtrahera $\log 1600$ från ekvationens båda sidor för att få 

    $x\cdot \log 1.28 = \log 2 + 7\cdot \log 1.28 \iff x = 7 + \frac{\log 2}{\log 1.28}.$

Visst, jag kan förfina mitt svar Yngve av min lösning som jag klistrade in här som bild. Problemet är att svaret ej är korrekt. Vi kanske har missförstått frågan? Kan det vara så? 

Albiki kom fram till rätt svar men med väldigt komplex lösningsmetod. Finns det ett enklare sätt att komma fram till svaret? Jag har skrivit ner Albikis metod men jag har på flera ställen svårt att förstå. Jag har aldrig arbetat med logaritmer på det sätt som Albiki gör i sin lösningsmetod. Kanske också därför jag tappar bort mig...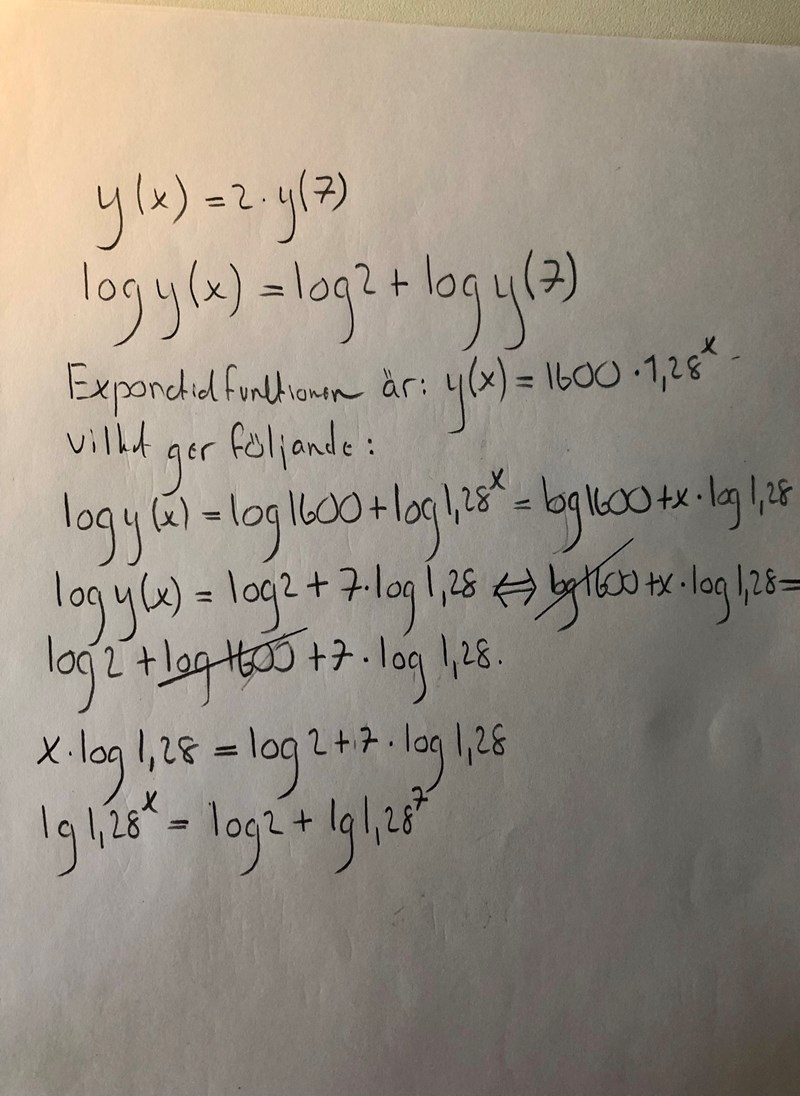

Natascha skrev:

Visst, jag kan förfina mitt svar Yngve av min lösning som jag klistrade in här som bild. Problemet är att svaret ej är korrekt. Vi kanske har missförstått frågan? Kan det vara så? 

Albiki kom fram till rätt svar men med väldigt komplex lösningsmetod. Finns det ett enklare sätt att komma fram till svaret? Jag har skrivit ner Albikis metod men jag har på flera ställen svårt att förstå. Jag har aldrig arbetat med logaritmer på det sätt som Albiki gör i sin lösningsmetod. Kanske också därför jag tappar bort mig...

Du gör fel på rad 6 där du har tappat bort en term.

Eftersom $y(7)=1600\cdot 1.28^7$ så är

$log(y(7))=log(1600)+log(1.28^7)=$

$=log(1600)+7\cdot log(1.28)$

------

Albikis och min lösning ger samma resultat.

Natascha skrev:

...

Problemet är att svaret ej är korrekt.

...

Vad menar du förresten med att svaret inte är korrekt?

Den lösning jag hintade om i detta svar, den lösning du själv skrev i detta svar och den lösning Albiki presentetade i detta svar ger alla samma resultat, nämligen ungefär 9.8 timmar, vilket är detsamma som 9 timmar och 48 minuter.

Vad står det i facit?

I facit står det: Ca 2,8 h (räknat från timme 7) 

Det är därför jag gång på gång skrivit att det blir fel. Våra uträkningar känns rätt och logiska men vem har rätt nu? Facit eller tre hjärnor? D.v.s. Jag, Yngve och Albiki? Gud vad invecklat detta blev nu. 

Vi kanske har missförstått uppgiften? :( 

Ni är helt överens. Du, Yngve och Albiki säger 9,8 timmar från start, facit säger 2,8 timmer från timme 7, d v s 7+2,8=9,8 timmar från start.

Ahaa, så vad skulle jag svara ifall denna fråga kom på ett prov? 2,8h eller 9,8h? I facit stod det (från timme 7) och det visste inte jag. När jag fick fram 9,8h så blir det lite missvisande när facit visar 2,8h. 

Ifall uppgiften vill ha svaret 2,8h då får dem skriva det i uppgiften, alltså, "räkna från timme: 7". Annars får dem nöja sig med att mitt slutgiltiga svar är 9,8h. 

Om man bara hade frågat hur lång tid det tar för antalet bakterier att fördubblas, så hade svaret varit entydigt (2,8 timmar). Det tar 2,8 timmar för antalet bakterier att fördubblas oberoende av antalet från början. (Man löser helt enkelt ekvationen 1,28^x=2.)

Stort tack för all hjälp! :)