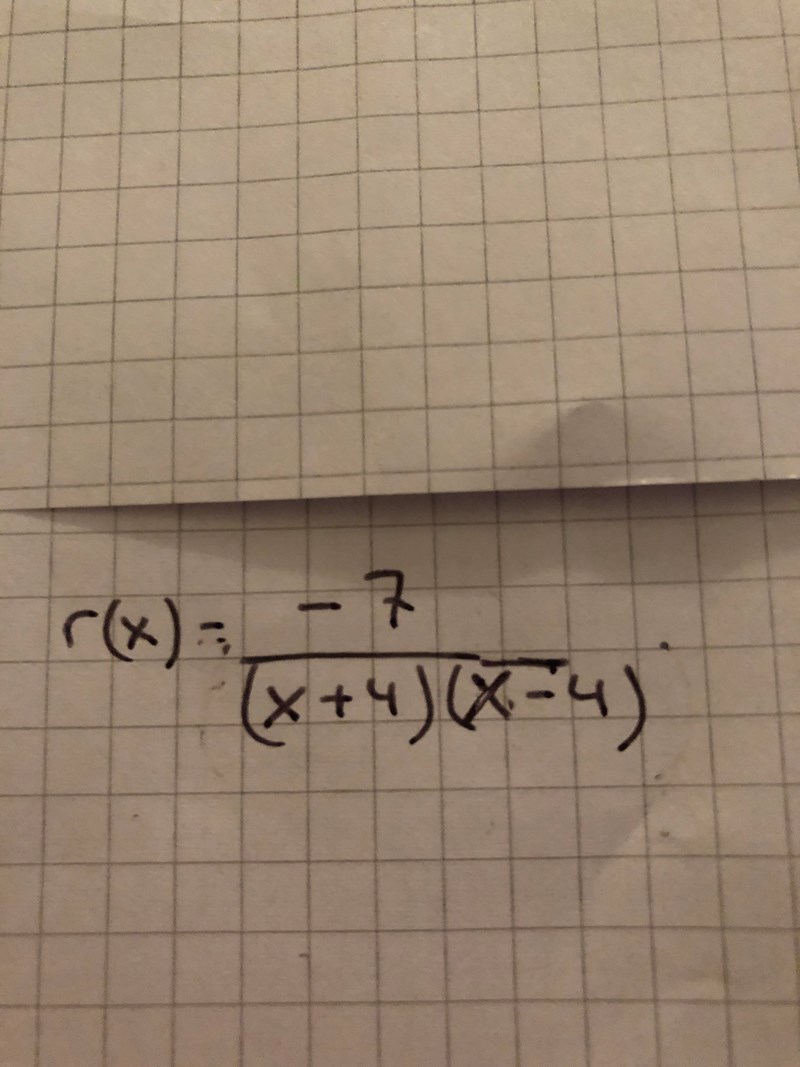Hur löser man detta rationella uttryck?

Ett vanligt uttryck som inte är definierat för x = 0 är 1/x. Skulle du kunna modifiera det så att det inte är definierat för x = ±4?

Hur menar du då?

$\frac{1}{x}$ är odefinierat för x = 0, eftersom nämnaren i ett bråkuttryck inte får vara noll. $\frac{1}{x-2}$ är odefinierat för x = 2, då nämnaren blir noll. Vilket uttryck skulle vara odefinierat för x = ± 4?

Jag ska alltså göra om (x+4)(x-4) och det kan ju skrivas på formen x^2-16

men sen hur gör jag sen? 

Om  r(x) har (x+4)(x-4) i nämnaren, vad ska det då stå i täljaren för att  r(3)  ska bli lika med 1?

-7?

Hur kom du fram till det?

Jag har villkoret r(3)=1 och jag vet nämnaren som är (x+4)(x-4) och det kan ju skrivas som x^2-16 och det är min nämnare och då blir täljaren -7 nee jag vet inte hur jag fick fram det nu, är förvirrad av rationella uttryck 

Det är rätt med -7 .  Hur fick du fram det?

Vad blir nämnaren för x=3?
Vad måste det då stå i täljaren för att kvoten ska bli lika med 1?

Eller som ekvation
Om  r(x) = $\frac{a}{(x+4)(x-4)}$, vad blir då  $a$  om  r(3) = 1 ?

Tänkte att om jag tar in r(3) i (x+4)(x-4) så blir det ju (3+4)(3-4) som blir 7* -1= -7? Men är det rätt tänkt?

moonlighttt skrev:

Tänkte att om jag tar in r(3) i (x+4)(x-4) så blir det ju (3+4)(3-4) som blir 7* -1= -7? Men är det rätt tänkt?

Ja. Du måste alltså ha -7 i täljaren för att f(3) skall bli lika med 1.

Är det svaret då?

Det är rätt tänkt.
För x=3 blir nämnaren  -7
För att kvoten ska bli 1 måste då även täljaren vara lika med -7.
Visst?

Enklast är då att sätta den lika med -7.

Men vi kan också låta den vara ett förstagradsuttryck,  kx+m.
Då ska kx+m också vara lika med  -7 för x=3,
dvs  k och m ska uppfylla villkoret  3k+m = -7.
Här finns det mycket att välja på...

Sätter vi k=0 får vi  m = -7  och kommer tillbaka till vår konstanta täljare. 
Sätter vi k=2 får vi  6 + m = -7  som ger m = -13
Täljaren kan alltså även vara  2x-13.
etc.

Men det blir rätt om jag sätter lösningen som -7/(x+4)(x-4), tack så mycket alla för hjälpen😊

moonlighttt skrev:

Men det blir rätt om jag sätter lösningen som -7/(x+4)(x-4), tack så mycket alla för hjälpen😊

Det saknas en pparentes runt hela nämnaren, annars blir det ett annat uttryck än det du har tänkt. (Om man skriver det med ett långt vågrätt bråkstreck behövs inte parentesen.)

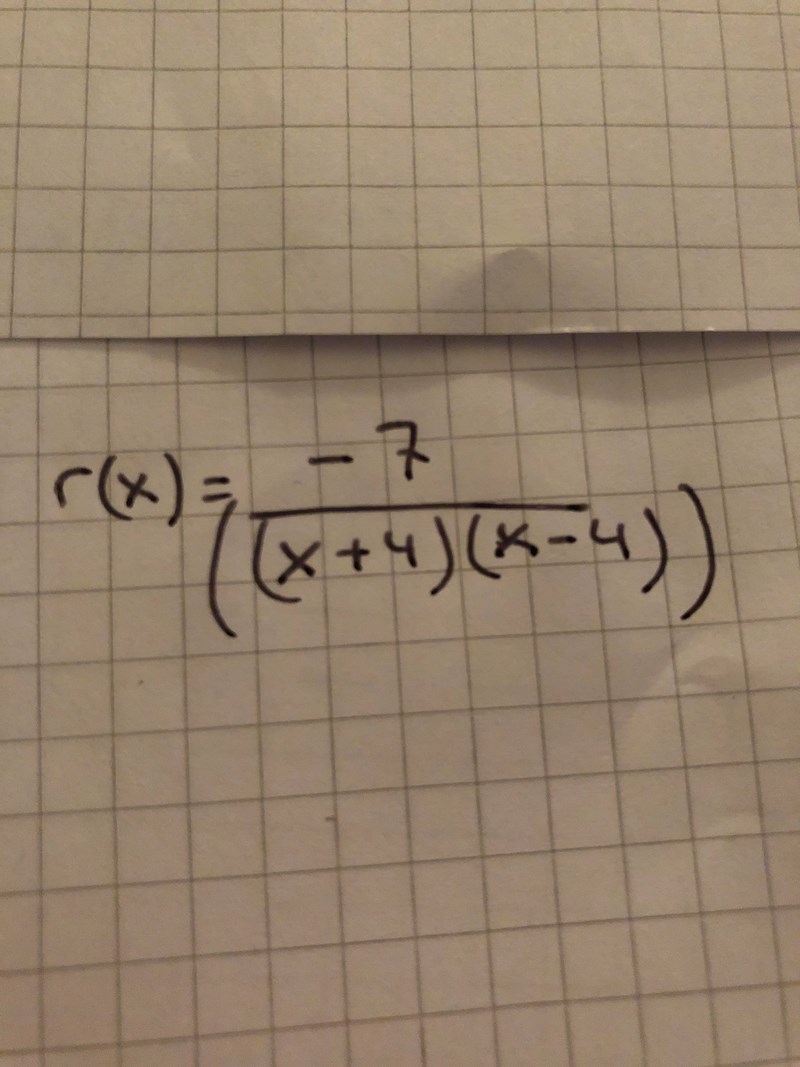Menar du så här?

moonlighttt skrev:

Menar du så här?

Nu har du skrivit det med ett långt vågrätt bråkstreck, så nu behövs inte de extra parenteserna. Det är när men skriver det med snett bråkstreck som parentesen behövs. -7/(x+4)(x-4) betyder $\frac{-7}{(x+4)}(x-4)$.

Jaha okej så jag kan skriva det så här då?