Hur löser man ut a och b för att funktionen och derivatan ska vara kontinuerlig?

Jag har försökt att göra frågan genom att derivera både funktioner (jag fick 1. x och 2. 2x+b) fast sedan vet jag inte vad jag ska göra efteråt. Jag testade med att göra olika ekvationer och annat fast ingenting funkar. Vad ska jag göra?

För att en funktion ska vara kontinuerlig i en punkt gäller det att både vänster- och högergränsvärdet existerar och att de är lika.

Eftersom även derivatafunktionen är en funktion så gäller det här att villkoren ska vara

$\lim_{x\rightarrow 2^{-}}f(x)=\lim_{x\rightarrow 2^{+}}f(x)$

$\lim_{x\rightarrow 2^{-}}f'(x)=\lim_{x\rightarrow 2^{+}}f'(x)$

Tack så himla mycket, jag förstår nu! Man ska väl göra 1=2x+b och sedan byta ut med x=2 för att få att b=-3 och sedan klura ut resten? I så fall, tack! :)

Ja, det stämmer.

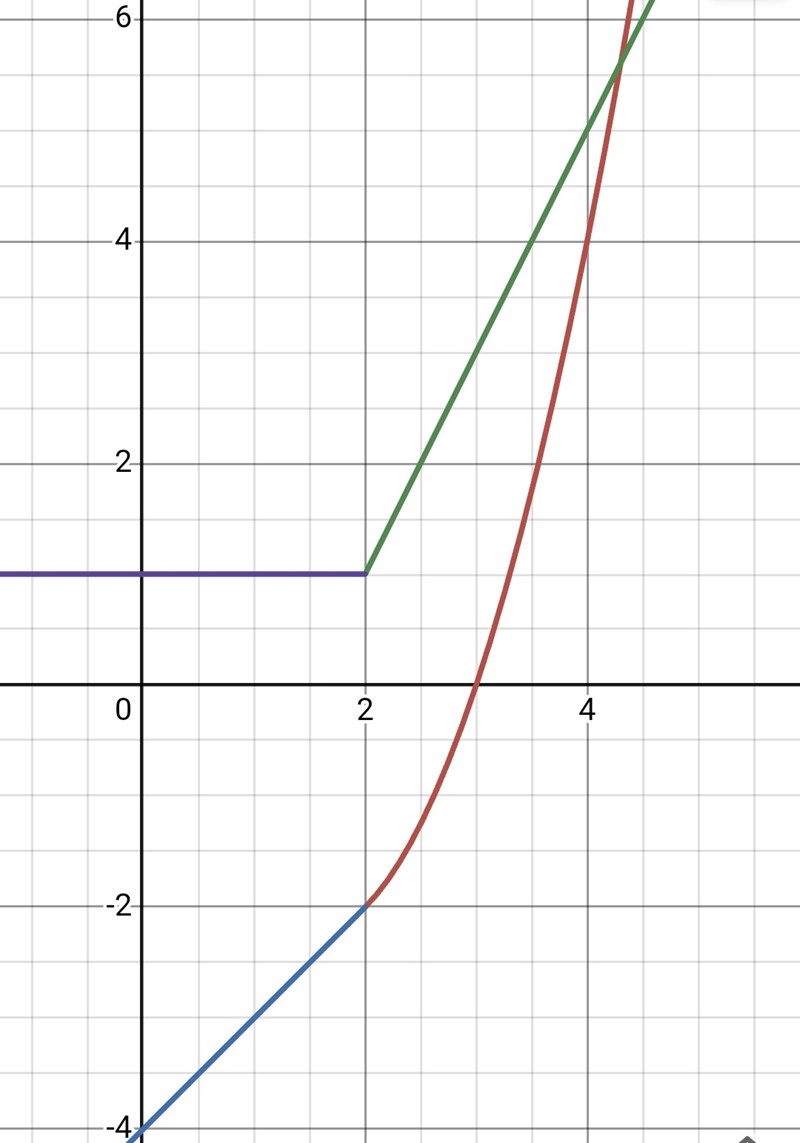
Graferna y = f(x) och y = f'(x) kommer att se ut så här:

Svara

Visa senaste svar