Hur löses detta?

Derivatans definition för funktionen $f$ i punkten $a$ är 

$\displaystyle f^\prime\left(a\right) = \lim_{h\to 0 }\frac{f(a+h)- f(a)}h$

0 i nämnaren ska du aldrig ha. Bakgrunden till uppgiften framgår inte. Måste därför fråga dig om ni har lärt er att derivera polynom? Här är två fkner som har f’(0)=2

f(x)=2x och

f(x)=2x+3

Kan du hitta flera?

Charlieb skrev:

Ange två olika funktioner som har derivatan 2 för x = 0

Då gjorde jag att det blev så:

lim h->0   (f(0+h) - f(0))/0

Då jag tänkte att x är 0 oavsett vilket då betyder att nämnaren måste vara 0, däremot har de i facits lösning skrivit nämnaren som h. Varför???

Jag tror uppg. är lite enklare än så. Du skall inse/veta att derivata = riktningstangent så om du ritar ett koordinatsystem så skall de sökta graferna ha riktningskoefficienten = 2 om x=0.

Nedan har jag ritat ett par riktningstangenter (men det finns ändligt många, alla parallella med varandra)

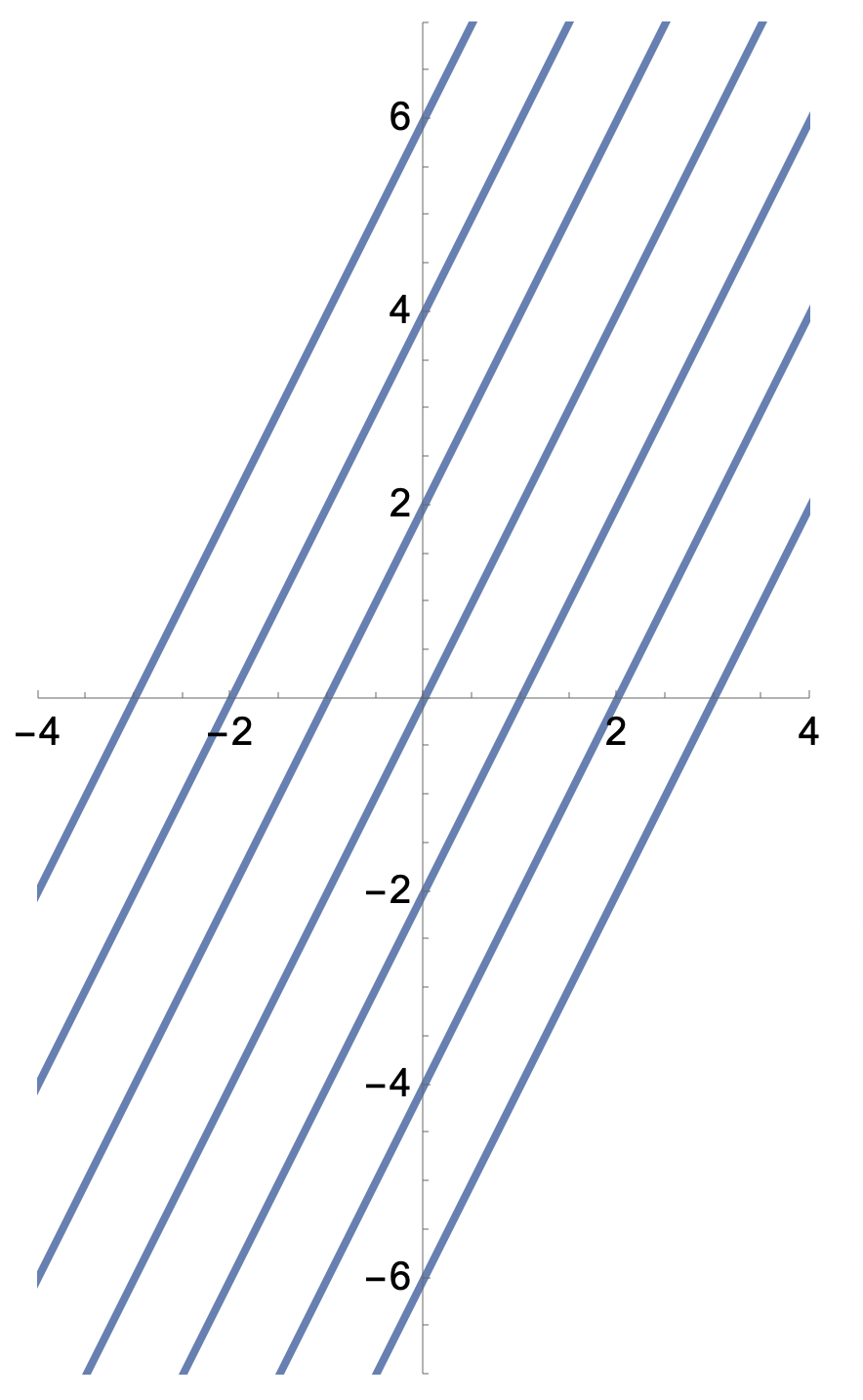
Vilka funktioner skulle du kunna rita in här? Skulle räta linjer gå?

Om inte en rät linje, vad skulle kunna passa då?

Notera att det är bara för x=0 som linjerna skall vara en tangent till kurvorna.