Hur många gånger ökar dina vinstchanser om du byter
Uppgift 5236:
Min lösning:
Facits svar:
Jag undrar verkligen över denna uppgift och om den som konstruerat den samt gjort facit vet vad den sysslat med. Denna uppgift är väl ett Monty Hall-problem: https://sv.wikipedia.org/wiki/Monty_Hall-problemet.
Vet jag inte A, men kan välja att få reda på B och C och att det är leksaksbilar i dem, så har jag två händelser som kan inträffa:
1. Jag har bilen men ruta D har inte bilen.
2. Jag har inte bilen men bilen finns bakom ruta D.
Själva poängen med spelet är att jag blir erbjuden att få se lucka B och C innan jag fått öppna min lucka. Säger jag "nej, jag vill öppna min lucka i stället för att öppna lucka D", så har jag 1/4 vinstchans. Men säger jag "Ja, jag vill öppna lucka D", så har jag två alternativ, antingen har jag bilen bakom min lucka och bilen finns därmed inte lucka D, och jag förlorar. Alternativ två är att jag inte har bilen men den finns bakom lucka D, och då vinner jag bilen. Detta är en vinstchans om 1/2
Min vinstchans ökar därmed från 1/4 till 1/2 om jag väljer lucka D. Därmed P(väljer att öppna lucka D efter att ha sett lucka B och C) / P (väljer att behålla lucka A) = (4/2) / (1/4) = 2. Två gånger ökar min vinstchans om jag byter från lucka A till lucka D när jag sett lucka A och C.
Jag undrar hur facit räknat, för hur jag än vrider och vänder på vad uppgiften menar så får jag inte det till att man t.ex. ska få se andra luckor än just B och C, tex kunna se C och D och sen välja om jag vill öppna lucka B. Då blir sannolikheten möjligen annorlunda, men uppgiften menar inte det vad jag kan se. Vete tusan hur denna uppgift konstruerats och om facits svar stämmer.
Alltihop bygger på att programledaren vet vilken dörr som döljer den riktiga bilen. Om du hade valt dörr D, skulle programledaren kunnat öppna dörr B och C, precis som nu, men om du hade valt lucka B skulle programledaren ha kunnat öppna dörr C och ANTINGEN dörr A eller D, men alltid den som innehöll en leksaksbil.
Smaragdalena skrev:Alltihop bygger på att programledaren vet vilken dörr som döljer den riktiga bilen. Om du hade valt dörr D, skulle programledaren kunnat öppna dörr B och C, precis som nu, men om du hade valt lucka B skulle programledaren hade kunnat öppna dörr C och ANTINGEN dörr A eller D, men alltid den som innehöll en leksaksbil.
Jag kan välja vilken bokstav som helst men det förändrar inte utgångspunkten att jag inte vet vad som finns bakom denna bokstav. Den kan ha bilen eller inte. Jag väljer bokstav A. Nu har jag 1/4 vinstchans om jag väljer att stanna med mitt val medan om jag väljer att byta till att få se de övriga två och byta till D har större vinstchans.
När jag byter från A till D har jag tre möjliga utfall.
1. Jag väljer att byta från A till lucka D. Programledaren öppnar lucka B och C. I dem finns leksaksbilar. Det får jag nu se. Programledaren öppnar min lucka. Där finns en bil. Programledaren öppnar lucka D, och där finns en leksaksbil. Jag förlorar bilen.
2. Väljer lucka A. Programledaren öppnar lucka B och D, där finns leksaksbilar. Programledare öppnar min lucka, där finns en leksaksbil. Bilen finns därmed i lucka C som programledare öppnar. Jag vinner bilen.
3. Väljer lucka A. Programledare öppnar lucka C och D som har leksaksbilar. I min lucka finns också en leksaksbil. Den riktiga bilen finns bakom lucka B som programledare visar. Jag vinner bilen.
Dessa är möjliga kombinationer av variablerna A, B, C och D. Om jag hade valt lucka B hade jag kunnat ha bilen bakom lucka B eller inte, och de övriga variablerna hade kombinerats med varandra på liknande sätt som jag visat. Vinstchansen hade blivit densamma, det vill säga 2/3.
Vinstchansen ökar från 1/4 till 2/3. Vinstchansen ökar med (2/3)/(1/4) = 2,67 gånger.
Det här problemet måste ändå vara ett https://sv.wikipedia.org/wiki/Monty_Hall-problemet. Det finns flera trådar på gamla pluggakuten som berör liknande ämne:
https://gamla.pluggakuten.se/forumserver/viewtopic.php?pid=132760
https://gamla.pluggakuten.se/forumserver/viewtopic.php?id=12820&id=12820/viewtopic.php
Nej det finns fyra möjliga fall. Bilen kan ju finnas bakom fyra olika dörrar.
Det är rätt enkelt om du tänker så här: Om bilen är i den lucka du första valde så förlorar du (1/4), är bilen i en annan lucka så vinner du (3/4).
Du har valt lucka A. Chansen att bilen är bakom lucka A är 25 %. Denna chans ökar eller minskar inte av att programledaren öppnar två luckor.
Om bilen hade funnits bakom lucka B, skulle programledaren ha öppnat lucka C och D. Om bilen hade funnits bakom lucka C, skulle programledaren ha öppnat lucka B och D. Dessa båda varianter är eliminerade, eftersom programledaren öppnade lucka B och C.
Chansen att bilen är bakom lucka A är fortfande 25 %. Hur stor är chansen att bilen är bakom lucka D?
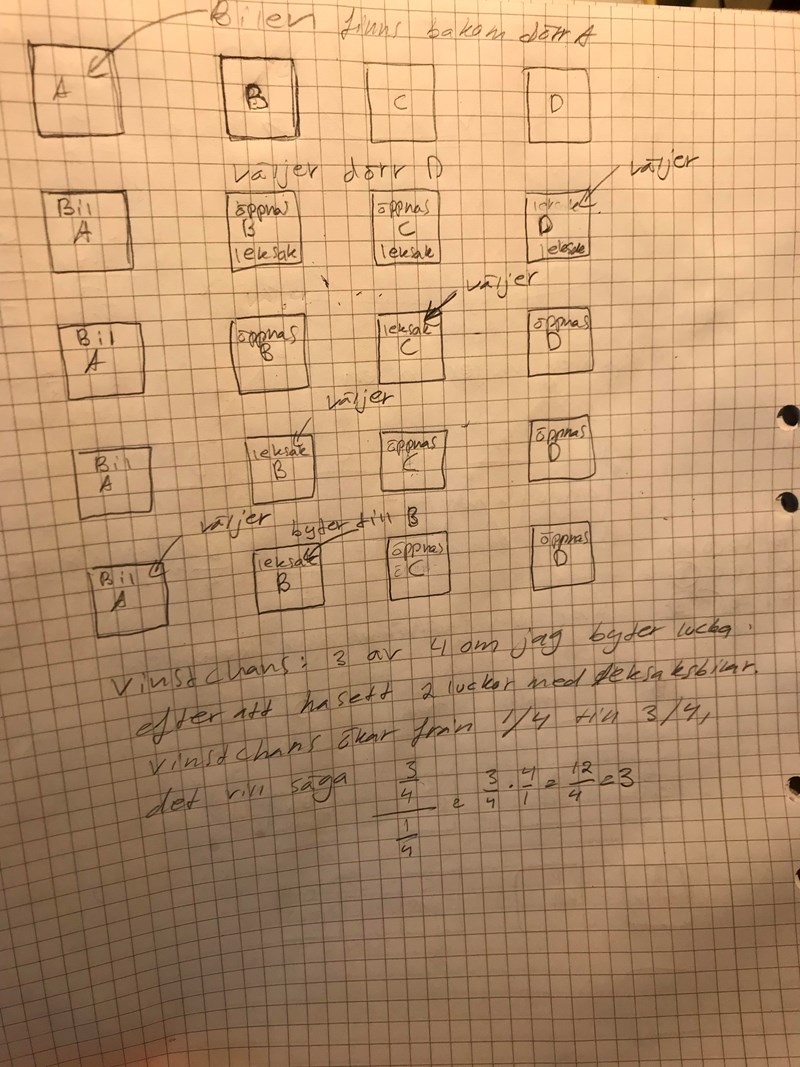Jag har gjort en figur med möjliga antal utfall. Det blir totalt fyra utfall med vinst i tre av dem. Problemet var ursprungligen att jag bytte plats på vilken lucka bilen var på. Bilen är från början i en lucka, och då kan man välja den luckan bilen är på. Bilen hoppar inte från lucka A till lucka D, t.ex. Där hade jag gjort ett antagande som inte stämde.
Smaragdalena skrev:Du har valt lucka A. Chansen att bilen är bakom lucka A är 25 %. Denna chans ökar eller minskar inte av att programledaren öppnar två luckor.
Om bilen hade funnits bakom lucka B, skulle programledaren ha öppnat lucka C och D. Om bilen hade funnits bakom lucka C, skulle programledaren ha öppnat lucka B och D. Dessa båda varianter är eliminerade, eftersom programledaren öppnade lucka B och C.
Chansen att bilen är bakom lucka A är fortfande 25 %. Hur stor är chansen att bilen är bakom lucka D?
Det är ungefär så här du kommer fram till en lösning Smaragdalena och även du antar jag, emilg:
Det här kan bevisas med:
"Ett sätt att troliggöra för den skeptiske att det är bättre att byta är att föreställa sig 100 olika dörrar, 99 getter och 1 bil. Sen när man gjort sitt val så öppnar spelledaren 98 av de andra dörrarna med getter bakom. Det finns då bara 2 dörrar kvar. Ska jag stå fast vid min första chansning eller byta? Det är ju då bara 1 på 100 att pricka rätt på direkten. Vid andra valet är det bara 2 dörrar kvar och fortfarande 1 på 100 att man råkade träffa rätt i första valet. Precis som i fallet ovan är det då (n-1)/n d.v.s. 99/100 att vinna om man byter."
https://sv.wikipedia.org/wiki/Monty_Hall-problemet
