Hur många nollställen?

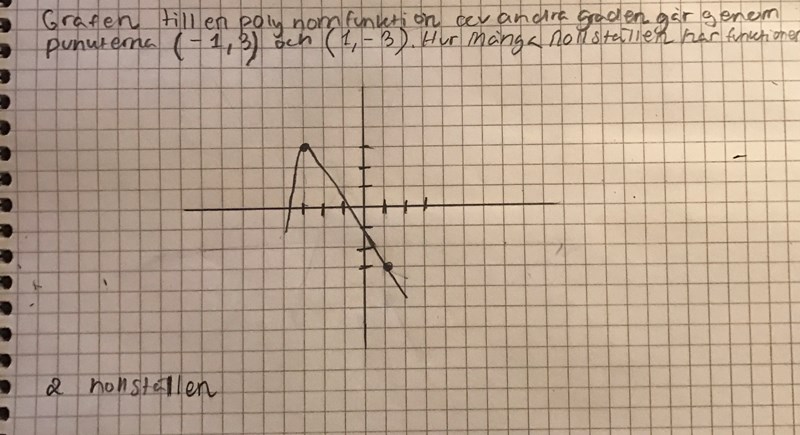
Kan man tänka såhär när man löser uppgiften? Att man ritar en graf och sedan ritar hur kurvan går igenom punkterna. Har jag gjort rätt?
Eller måste jag göra en ekvation och lösa uppgiften?
Du kan inte riktigt resonera så som du gjort. Resonemanget ska gälla för alla andragradspolynom som uppfyller kraven, titta här: https://www.desmos.com/calculator/egfu2qnbzz, ändra lite på k-värdet så kommer du få olika andragradskurvor som går genom de angivna punkterna.
Som du ser så kommer du alltid få två lösningar, men kan du försöka göra ett generellt argument varför det alltid kommer vara så?
Ska jag använda formeln kx+m, är det den du menar?
Nej, utan om man skulle beskriva en andragradskurva så skulle man kunna klassificera dem som
- De börjar med att gå nedåt och sedan vänder de och går uppåt.
- De börjar med att gå uppåt och sedan vänder de och går nedåt.
En andragradskurva kommer hamna i någon av dessa kategorier.
Nu vet du att i kategori 1 så kommer kurvan behöva gå ned genom punkten (-1, 3) och sedan nedåt mot (1, -3), någonstans däremellan så måste den ju passera y = 0, alltså ett nollställe. Sedan efter, eller innan, den passerat punkten (1, -3) så måste den vända och börja gå uppåt igen, då kommer den igen passera y = 0, alltså ett till nollställe. Så då har den alltså två nollställen.
Kan du resonera på ungefär samma sätt för kategori 2?


