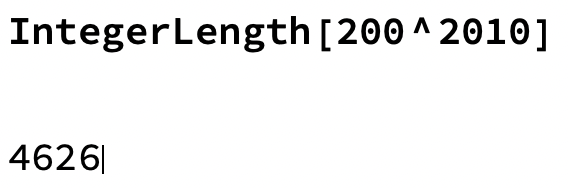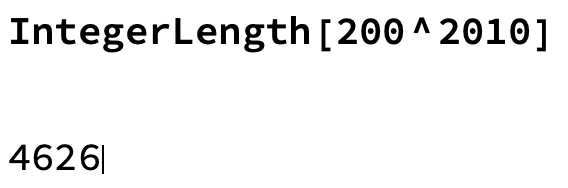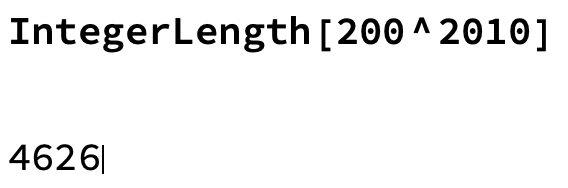Hur många siffror är det i talet?

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Tyra_S skrev:

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Ja, det är väldigt exakt. Vad betyder streckad fyrkant runt "34"? Digitala verktyg?

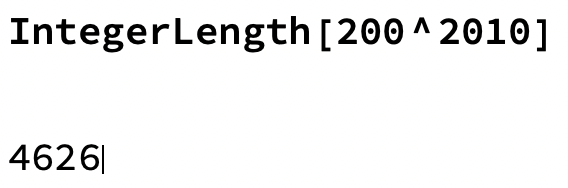
Tyra_S skrev:

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Jag håller med om att det är märkligt. Ser att Trinity2 precis skriver, så det kanske kommer en briljant förklaring. Min hjärna är i alla fall för trött för att komma på något listigt.

Trinity2 skrev:

Tyra_S skrev:

Visa föregående citat

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Ja, det är väldigt exakt. Vad betyder streckad fyrkant runt "34"? Digitala verktyg?

Ja precis! Det står för digitala verktyg!

sictransit skrev:

Tyra_S skrev:

Visa föregående citat

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Jag håller med om att det är märkligt. Ser att Trinity2 precis skriver, så det kanske kommer en briljant förklaring. Min hjärna är i alla fall för trött för att komma på något listigt.

Hahah jag fattar! Tack för hjälpen ändå!

sictransit skrev:

Tyra_S skrev:

Visa föregående citat

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Jag håller med om att det är märkligt. Ser att Trinity2 precis skriver, så det kanske kommer en briljant förklaring. Min hjärna är i alla fall för trött för att komma på något listigt.

Tror kanske att man skall först inse att

100^2010 = 10^4020

vilket ger 1+4020=4021 siffror

Sedan måste man fokusera på 2^2010 som har(!) 606 siffror.  Men jag ser inget direkt mönster för att finna det värder, rakt av.

Tyra_S skrev:

Trinity2 skrev:

Visa föregående citat

Tyra_S skrev:

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Ja, det är väldigt exakt. Vad betyder streckad fyrkant runt "34"? Digitala verktyg?

Ja precis! Det står för digitala verktyg!

Aha, men det måste till rätt bra verktyg för att räkna ut detta - tror jag. Finns "Antal siffror" som inbyggd funktion i dagens räknare? Kanske TI Inspire-appen?

Trinity2 skrev:

sictransit skrev:

Visa föregående citat

Tyra_S skrev:

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Jag håller med om att det är märkligt. Ser att Trinity2 precis skriver, så det kanske kommer en briljant förklaring. Min hjärna är i alla fall för trött för att komma på något listigt.

Tror kanske att man skall först inse att

100^2010 = 10^4020

vilket ger 1+4020=4021 siffror

Sedan måste man fokusera på 2^2010 som har(!) 606 siffror.  Men jag ser inget direkt mönster för att finna det värder, rakt av.

Exakt! Det var det jag kunde konstatera också, men jag antar att det då måste innebära att man ska ta hjälp av något digitalt verktyg som kan räkna ut det??

Trinity2 skrev:

Tyra_S skrev:

Visa föregående citat

Trinity2 skrev:

Tyra_S skrev:

Visa föregående citat

sictransit skrev:

Har du börjat med logaritmer? Annars skulle jag säga att uppgiften är väldigt svår att lösa exakt. Åtminstone kommer jag inte på något sätt rakt av. 

Man kan bilda sig en uppfattning om storleksordningen eftersom 2¹⁰=1024, alltså ungefär 10³. 

Tack för svar! Nej, jag har inte börjat med logaritmer än. Jag tänker att det nog är som du säger, men det är ändå konstigt eftersom det i facit står att svaret är 4 626. Om man skulle ”gissa” sig fram borde det ju inte stå så exakt?

Ja, det är väldigt exakt. Vad betyder streckad fyrkant runt "34"? Digitala verktyg?

Ja precis! Det står för digitala verktyg!

Aha, men det måste till rätt bra verktyg för att räkna ut detta - tror jag. Finns "Antal siffror" som inbyggd funktion i dagens räknare? Kanske TI Inspire-appen?

Ingen aning faktiskt! Jag ska kolla upp det!

I GeoGebra hittar jag ingen funktion rakt av, så då är åtminstone jag tillbaka till logaritmerna igen. :-)

$⌊2010\times {\log }_{10}\left(200\right)⌋+1=4626$

För det behöver man bara en simpel miniräknare, samt kunskap om logaritmer. Så då var vi tillbaka där vi började. 

Fråga din lärare hur den är tänkt att lösas (utan logaritmer) om du har lust. Jag är lite nyfiken.

sictransit skrev:

I GeoGebra hittar jag ingen funktion rakt av, så då är åtminstone jag tillbaka till logaritmerna igen. :-)

$⌊2010\times {\log }_{10}\left(200\right)⌋+1=4626$

För det behöver man bara en simpel miniräknare, samt kunskap om logaritmer. Så då var vi tillbaka där vi började. 

Fråga din lärare hur den är tänkt att lösas (utan logaritmer) om du har lust. Jag är lite nyfiken.

Ja, hahha precis! Jag har inte lärt mig om logaritmer än, men det verkar ju som att det är den rimligaste lösningen. Jag ska fråga min lärare så fort som möjligt! 

Trinity2 skrev:

Tror kanske att man skall först inse att

100^2010 = 10^4020

vilket ger 1+4020=4021 siffror

Sedan måste man fokusera på 2^2010 som har(!) 606 siffror.  Men jag ser inget direkt mönster för att finna det värder, rakt av.

$$\begin{gathered} 2^{10}=1024\approx 1000={10}^3 \\ {2}^{2010}={\left(2^{10}\right)}^{201}\approx {\left({10}^3\right)}^{201}={10}^{603} \end{gathered}$$

Men det saknas ett par siffror i alla fall.

MaKe skrev:

Trinity2 skrev:

Tror kanske att man skall först inse att

100^2010 = 10^4020

vilket ger 1+4020=4021 siffror

Sedan måste man fokusera på 2^2010 som har(!) 606 siffror.  Men jag ser inget direkt mönster för att finna det värder, rakt av.

$$\begin{gathered} 2^{10}=1024\approx 1000={10}^3 \\ {2}^{2010}={\left(2^{10}\right)}^{201}\approx {\left({10}^3\right)}^{201}={10}^{603} \end{gathered}$$

Men det saknas ett par siffror i alla fall.

Snyggt! Man får nog tänka att det inte går att lösa helt exakt! Tack för hjälpen!

Bad ChatGPT5 lösa den utan logaritmer:

tomast80 skrev:

Bad ChatGPT5 lösa den utan logaritmer:

Tack!

tomast80 skrev:

Bad ChatGPT5 lösa den utan logaritmer:

Intressant! Det där ser trovärdigt ut. Den räknar inte 100% rätt, men hamnar på rätt tiopotens och får rätt svar.

Metoden är dock inget man rimligtvis kan förvänta sig på Matte 1, även om den visar att man faktiskt inte behöver ta till logaritmer. Däremot behöver man en miniräknare.

Streckad ram kring uppgiftsnumret tyder på att "enkla" miniräknare räcker:

Varken GeoGebra eller TI-84 klarar av att beräkna $2^{2010}$, men det går bra med $2^{201}$.

I GeoGebra kan man utnyttja kommandot Grundpotensform(2^201) för att få fram att $2^{201} \approx 3,213876\ldots \cdot 10^{60}$

Därefter ger kommandot Grundpotensform(3.213876^10)${}\approx 1.176\ldots \cdot 10^5$.

Allt får nu kombineras ihop:

$200^{2010} = (2^{201})^{10} \cdot 10^{4020} \approx (3,213876\ldots \cdot 10^{60})^{10} \cdot 10^{4020}$

$\approx 3,213876^{10} \cdot 10^{4620} \approx 1,176\ldots \cdot 10^5 \cdot 10^{4620} \approx 1,176\cdot 10^{4625}$

vilket visar att det finns 4626 siffror.

sictransit skrev:

tomast80 skrev:

Bad ChatGPT5 lösa den utan logaritmer:

Intressant! Det där ser trovärdigt ut. Den räknar inte 100% rätt, men hamnar på rätt tiopotens och får rätt svar.

Metoden är dock inget man rimligtvis kan förvänta sig på Matte 1, även om den visar att man faktiskt inte behöver ta till logaritmer. Däremot behöver man en miniräknare.

Tänkte exakt likadant, utan miniräknare går det bara att räkna antalet siffror approximativt.

Sådär ja!

Nu är den löst helt utan digitala hjälpmedel, men med logaritmer.

Som diskuterats tidigare behöver vi lösa följande ekvation:

${200}^{2010}={10}^x$

Antalet siffror blir $⌊x⌋+1$, alltså x avrundat nedåt +1. Exempel: ${10}^{2,1}\approx 126$, där vi avrundar 2,1 till 2 och med +1 får 3 siffror.

Vi använder logaritmer för att skriva om ekvationen:

$$\begin{gathered} {200}^{2010}={10}^x \\ 2010\times \log 200=x\times \log 10=x \end{gathered}$$

Kan vi bara hitta ett värde på log 200 så återstår bara en multiplikation vi klarar med penna och papper.

Vi ställer in 2 på vår räknesticka (röda pilen) och får logaritmen vid den gröna pilen.

Jag läser av: $\log 2\approx 0,301$.

Det ger oss att: $\log 200\approx 2,301$

Då återstår bara multiplikationen med 2010, vilket ger oss svaret:

$x\approx 4625,01 \Rightarrow ⌊x⌋+1=\boxed{4626}$

PS. Nej, riktigt så gammal är jag inte. Min far satte den i handen på mig när jag gick i gymnasiet. Han tyckte det var det rätta sättet att på riktigt förstå logaritmer. Logaritmlagarna får man gratis, eftersom de är en förutsättning för att använda den.

Vill man inte använda så moderna hjälpmedel som en räknesticka går det förstås bra med en logaritmtabell. Det var vad man hade innan den uppfanns. (Sedan kom miniräknarna tidigt 70-tal och allt annat blev omodernt.)

Henry Briggs (1561-1630) klurade ut logaritmerna med bas tio, de vi kallar "tio-logaritmer".

Här är ett utdrag ur hans tabellverk Logarithmorum Chilias Prima från 1617:

$\log 2\approx 0,3010$

Varenda logaritm var räknad för hand! Ja, för hur skulle man annars göra?

400 år sedan! Inte så illa, eller hur?

(Henry Briggs, Public domain, via Wikimedia Commons)