Hur räknar jag ut X och Y i denna bild?

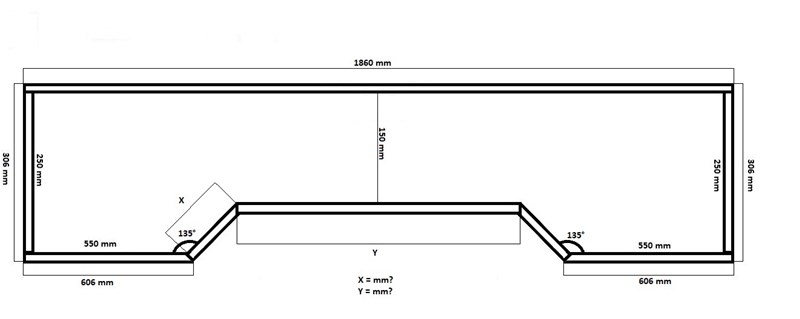
Det behövs inga gymnasiekunskaper för det här - för visst läser man Pythagoras sats på högstadiet?

Rita en linje rakt upp från den vänstra av vinklarna som är märkt 135 grader och en vågrät linje strax ovanför, så att det bildas en rätvinklig triangel med hypotenusan x. Eftersom vad-det-nu-är är symmetrisk, finns det tillräckligt med info för att beräkna längden av de båda kateterna (och då får du samtidigt fram värdet på sträckan y). Använd sedan Pythagoras sats. Om det här inte räcker - visa hur långt du ahr kommit och fråga igen.

Eftersom jag kan i alla fall lösa ut va en av kateterna är (100 mm) och har gradvinkel i triangeln (45 grader) så måste jag väll använda mig utav Trigonometri för att lösa va den andra katetern är eller tänker jag fel då?

Kan detta stämma, 100 / cos 45 = 190.36 för att få ut hypotenusan? Eftersom jag bara vet av en katet och vinkel i triangeln

Det behövs ingen trigonometri för att lösa den här uppgiften. Eftersom du får två  45-90-45-trianglar är det lätt att beräkna hur lång var och en av de korta sidorna i den rätvinkliga triangeln är - en sådan sida plus 150 mm skall bli 250 mm.

Rätta mig gärna om detta blev helt galet. Vill helst slippa kapa fel XD

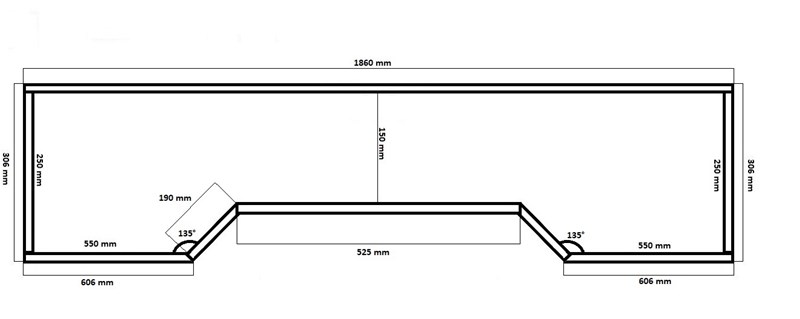
Nej, de sneda sidorna skulle (rent matematiskt) bli lite mer än141 mm långa, men i det här fallet räcker inte matematiken (bara) till. Eftersom det handlar om lister (gissar jag) blir allting krångligare, eftersom de ha ren bredd. Om du försöker kapa listerna till en 135-graders vinkel genom att såga av den ena i 90 grader och den andra i 45 grader kommer bitarna inte att passa ihop - den sneda ytan kommer att bli längre än den raka. Om det handlar om snickeriarbeten skulle jag rekommendera att du ritar väldigt noggrannt i skala 1:1 och mäter på den ritningen. Beroende på vad du har för form på listerna blir det troligen inte snyggt i de yttersta hörnen heller - där skulle jag välja att kapa av båda listerna i 45 graders vinkel, för då kommer de att passa ihop snyggt.

Jag ska ta och försöka skaffa ett 3dprogram och göra ritning där ihop med att få så rätt som möjligt. Tack för hjälpen och jag ska dona vidare med detta projekt. Det var ett bra tag sen man höll på med denna typ av matte XD Bara som avslutning kan du skriva ned formeln och svaret så jag vet vad jag gör för fel

Tack igen

Hypotenusan h i en triangel med sidan 100 mm blir 141,4 mm lång eftersom $h=\sqrt{100^2+100^2=100 \cdot sqrt2$.

Hej, först och främst vet jag att den här posten är nästan en månad gammal men jag har gått igenom den här uppgiften och hittade två olika svar som jag kommer att diskutera, båda är väldigt lika men skillnaden är att i den första räknar jag värdena som om tjockleken på linjerna skulle inte finnas och i den andra tänker jag på att det spelar roll hur tjocka linjerna är.

I det första alternativ hittade jag först avståndet mellan bottnen på figuren och linjen där Y fanns vilket blev 100 mm. Om man ritar vågräta linjer vid Y-linjens kanter får man två trianglar, som är rätvinkliga samt likbenta eftersom två av deras vinklar är 45 grader dvs, de två kateterna i trianglarna är likadana. Med avståndet mellan bottnen och Y kan man bestämma hur långa är kateterna, alltså, 100 mm. Då använder man Pythagoras teorem: ${100}^2+{100}^2=z^2$ och får $z=100\sqrt{2}$ som är ungefär 141,42 mm och det är X-värdet. Med längden på kateterna i de trianglarna, som har redan varit räknat (100 mm) Blir det enkelt att hitta Y-värdet, genom att subtrahera sidan uppe figuren (som är 1860 mm) med de båda linjerna som är 606 mm långa och de två nedläggande kateterna från trianglarna (100 mm var och en) blir det: 1860-1212-200= 1860-1412= 448 mm. Då har vi X=141,42 mm och Y=448 mm. I det andra alternativet där jag antar att tjockleken i linjerna hos figuren spelar roll, vilket jag tycker borde vara så. För att räkna tjockleken hos linjerna gjorde jag såhär: den yttre linjen i vänster eller högern sidan av figuren minus den som finns inre, 306-250=56 och delar den med två och får 28 mm tjocklek om man antar att linjerna är lika tjocka. Det gör att avståndet mellan bottnen och Y-linjen blir kortare än i alternativ 1. Den blir i det här fallet 72 mm, då blir formeln för X-sträckan: ${72}^2+{72}^2=x^2$ som kan lösas $x=72\sqrt{2 }$ som är ungefär lika med 101,82 mm. Y-värdet ändras också eftersom längder på kateterna blir olika, då blir formeln för att hitta Y vara:$1860-1212-144=1860-1356=504$ mm. Alltså X=101,82 och Y=504 i det här fallet. 

Slutsats det blev olika resultat när jag tänkte på de två sätt, jag tycker att den andra alternativ (x=101,82 mm och y=504 mm) låter mer rimligt än den första (x=141,42 mm och y=448 mm) eftersom tjockleken in linjerna spelar en viktig roll här. Det här var mitt svar, hade jag fel på något? det kan ni diskutera. =)

Hej!

Figuren tycks indikera att

    $\displaystyle 550 + X\cos 45^\circ + Y + X\cos 45^\circ + 550 = 1860-56$

och att

    $\displaystyle 250 = 150 + X\sin 45^\circ.$

Det gäller att $\sin 45^\circ = \frac{1}{\sqrt{2}} = \cos 45^\circ$ så den andra ekvationen säger att

    $X = \frac{250-150}{1/\sqrt{2}} = \sqrt{2} \cdot 100 \approx 141$ millimeter.

Den första ekvationen ger den sökta längden $Y$.

    $\displaystyle Y = 1860-56-1100-2X\cos 45^\circ = 704-2\sqrt{2}\cdot 100 \cdot \frac{1}{\sqrt{2}} = 704-200 = 504$ millimeter.